
Урок "Подмножество"

Краткое описание документа:
Как известно, множество является одним из важнейших элементов алгебры, а точнее – теории множеств. Это понятие не имеет строгого определения в силу своей аксиоматичности и фундаментальности, и передается на словах, как некий набор математических реальных чисел. Множества могут быть разными, включать большой спектр различных постоянных и переменных элементов, либо же вообще быть пустыми. Множество всех существующих определяемых чисел является бесконечным математическим множеством. А эфемерное множество, не содержащее никаких значимых объектов, именуется пустым.
В зависимости от свойств объектов, допускается выделение особых групп внутри множества. Например, рассмотрим бесконечное множество натуральных целых чисел, обозначенное как N. Выделим из него такие элементы, которые будут отвечать заданным свойствам – четность, и расположение в интервале от 1 до 11. Это числа 2, 4, 6, 8, 10. Эти пять элементов формируют особую группу, отвечающую общим свойствам, заданным в условии. При этом все члены группы принадлежат множеству натуральных чисел. Такие внутренние объединения именуются подмножествами.
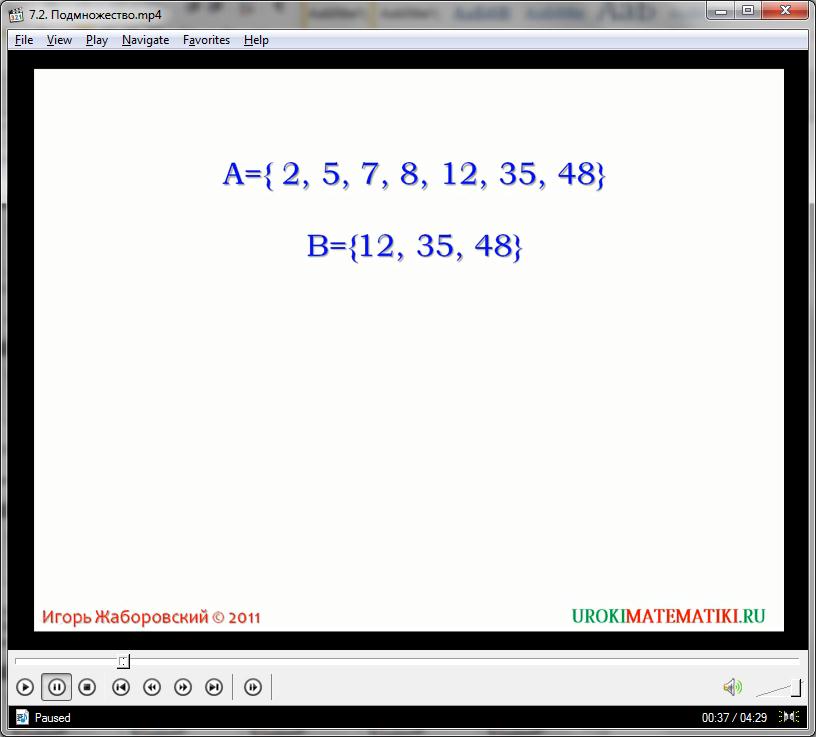
Подмножество – это внутренняя группа элементов множества, все члены которой строго принадлежат данному множеству. Этот набор также принято обозначать большими латинскими группами – например, вышеуказанный пример из пяти элементов можно обозначить, как подмножество S. Стоит сразу отметить, что любое подмножество само по себе является независимым множеством. Приставка под- обозначает только факт принадлежности всех членов данной группы к более широкому набору элементов, относящихся к большому множеству. С другой стороны, такое объединяющее множество именуют надмножеством. Из нашего примера следует, что множество N натуральных чисел включает подмножество S чисел, отвечающих условиям четности, и расположения в интервале (1, 11). Иначе можно сказать, что множество S, состоящее из пяти натуральных чисел, относится к надмножеству N, содержащему все натуральные числа.
Взаимоотношения между различными группами элементов могут быть самыми разнообразными. То же множество натуральных чисел может включать практически бесконечное количество различных группировок – подмножеств. В фундаментальном определении теории множеств чисел существует два основных базиса: само множество, как набор элементов, и свойства, задающие этот набор, или описывающие его. Собственно говоря, эти свойства позволяют не только ограничить набор чисел во множестве, но и включить его в состав какого-либо надмножества либо же выделить из него подмножество.
В нашем видеоуроке мы также рассмотрим взаимосвязь между двумя различными независимыми множествами. Например, рассмотрим следующие множества произвольных чисел:
S: 2, 5, 6, 7, 9, 12
D: 2, 5, 6, 7
F: 2, 5, 6, 7, 9, 12
Все элементы множества D встречаются среди членов множеств и S и F. Можно сказать, что D является подмножеством множества S, и подмножеством множества F.
С другой стороны, все элементы множества S совпадают с элементами множества F. Соответственно, и наоборот. Можно обозначить, что S является подмножеством для F, а F, в свою очередь, является подмножеством для S. Но чаще всего говорят, что множества просто равны между собой.
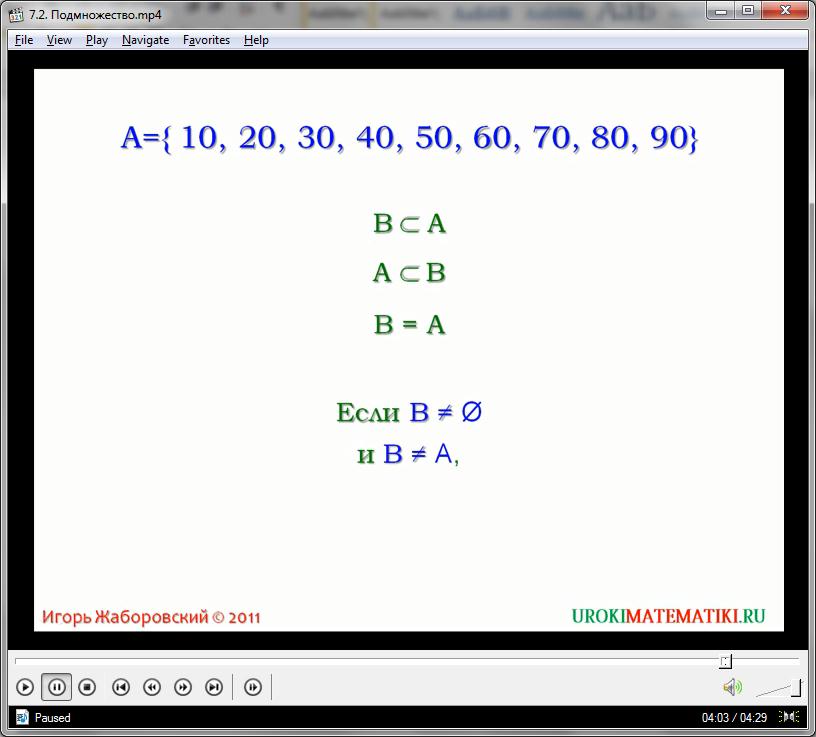
Если любое подмножество А не равно пустому множеству (т.е. содержит хотя бы один элемент), и при этом не равно другому множеству В, то считается, что подмножество А является собственным подмножеством для В. Пустое множество является собственным подмножеством для любого множества, кроме самого себя. С другой стороны, практически все реальные множества являются подмножествами бесконечного множества действительных чисел.
На геометрии подмножества отображаются двумя способами. Собственно геометрический представляет собой линейно-интервальный метод отображения наборов чисел на горизонтальной прямой. Чертится прямая (теоретически бесконечная – как отображение бесконечного надмножества чисел), на ней откладываются заданные числовые отрезки. Например, множество целых чисел от 2 до 10 образуют отрезок АС. Множество четных чисел, состоящих, например, из 2, 4, 6 являются подмножеством для АС, и задаются более коротким отрезком АВ, лежащим на той же прямой, на некотором участке АС.
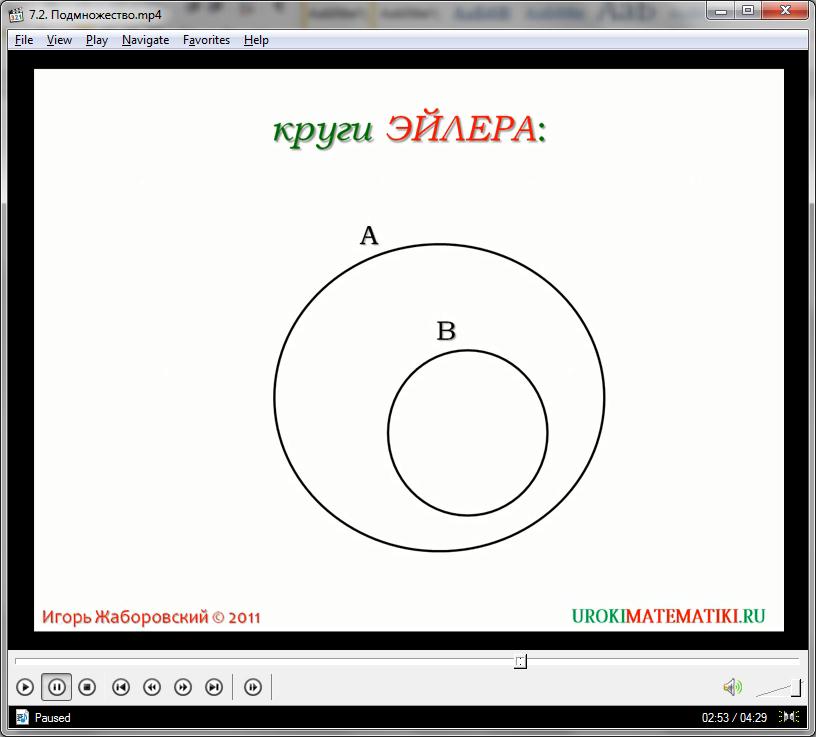
Но более удобным изображением подмножества являются круги Эйлера. В данном случае, каждое множество представлено правильным кругом. Подмножества выделяются меньшими кругами, вложенными в большой круг. Если подмножество равно самому множеству, то круги совпадают между собой. Если группа элементов не соотносится с каким-либо множеством, то круг группы выходит за пределы этого множества.
| Автор | |
|---|---|
| Дата добавления | 25.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13862 |
| Номер материала | 440 |