
Урок "Деление и дроби"

Краткое описание документа:
Видеоурок «Деление и дроби» представляет наглядный материал для урока математики по данной теме. Задача данного урока – сформировать понятие о связи между операцией деления и представлением результата деления в виде дроби, научить представлять натуральные числа в виде дробей, пользоваться правилом деления суммы на число при решении выражений. В ходе демонстрации подробно рассматриваются на иллюстрированных примерах операции над дробями, связь между операцией деления и дробью. Благодаря мультимедийным возможностям, материал подается понятно для учеников, с подробным объяснением. Этот видеоурок может применяться вместо объяснения учителя по данной теме, а также сопровождать объяснение учителя наглядным материалом. Использование наглядного пособия дает возможность повысить эффективность обучения, способствует лучшему запоминанию и усваиванию материала.
В демонстрации учебного материала используются приемы, улучшающие наглядность материала, способствующие его запоминанию. Это выделение текста цветным и жирным шрифтом, использование в объяснении материала иллюстраций, анимационных эффектов, дополнение видео озвучиванием – важными комментариями учителя. Также демонстрация видео помогает акцентировать внимание учащихся на обучении, удерживать их внимание на освоении предмета.
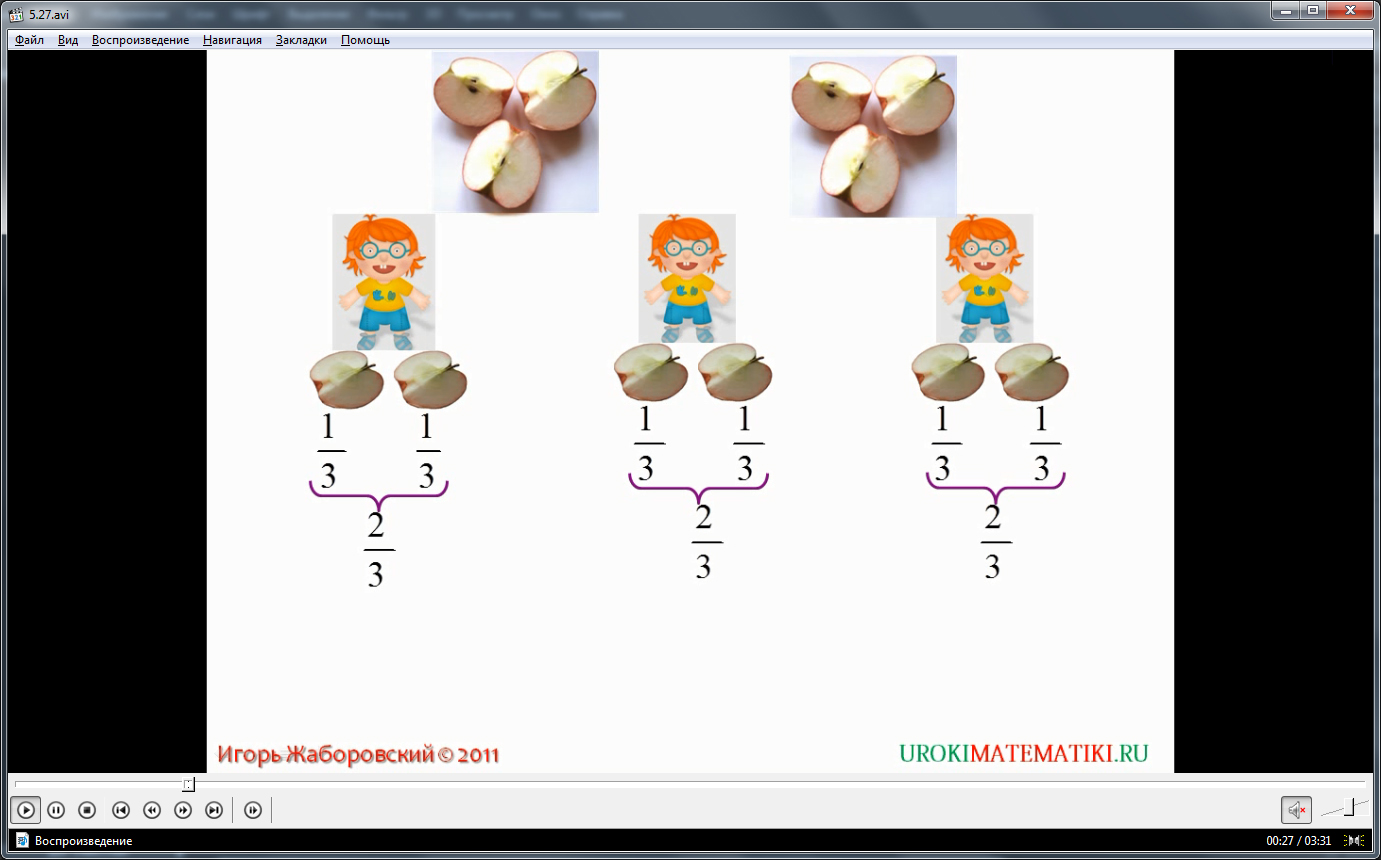
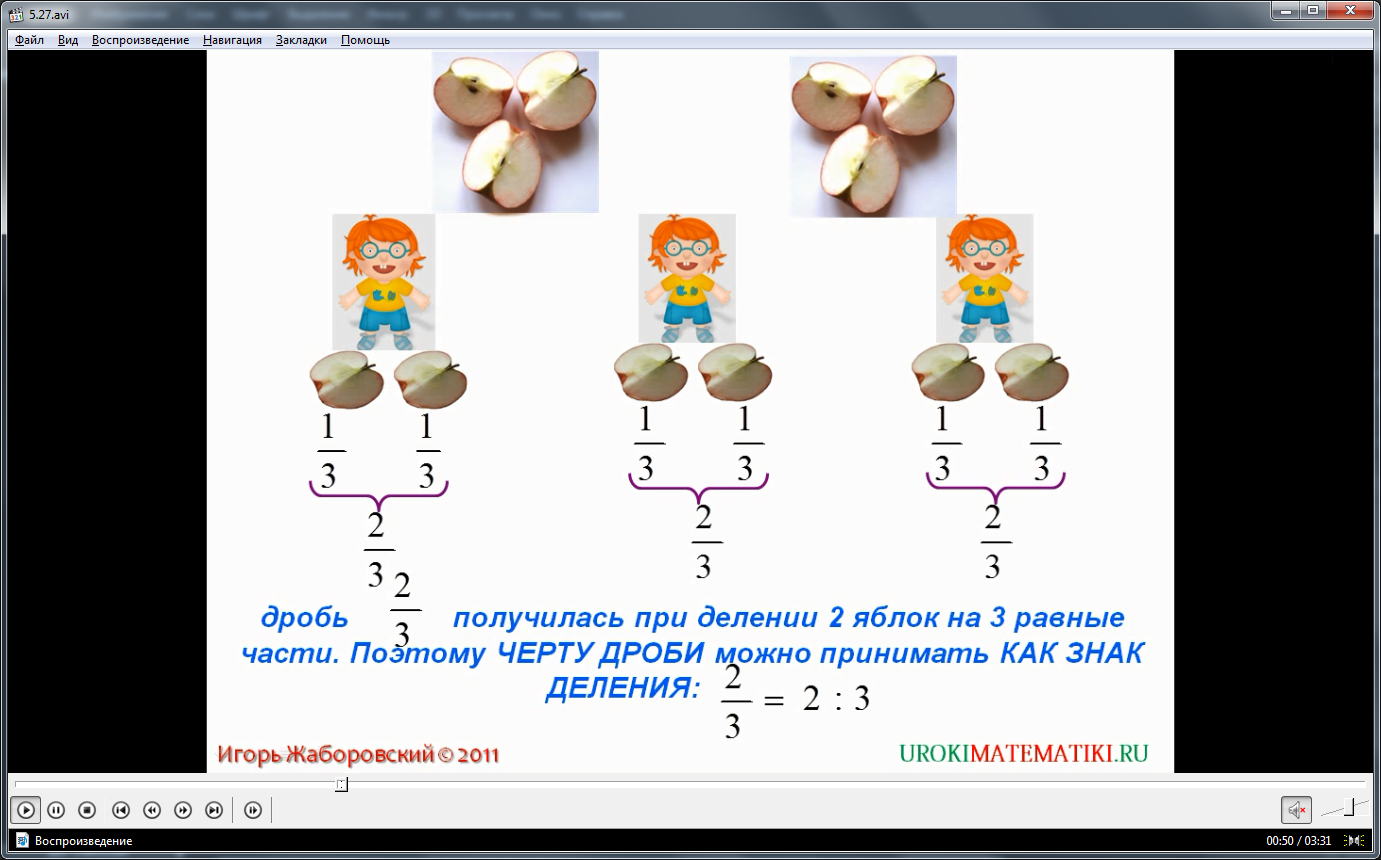
Видеоурок начинается с представления темы урока. Затем с помощь иллюстраций и анимации представляется правило деления целого на части и формирование дробей. На рисунке демонстрируется два одинаковых яблока. Чтобы поделить яблоки поровну между тремя детьми, необходимо каждое из этих яблок разделить на три равные части, так как иначе эти яблоки невозможно разделить между тремя детьми. На рисунке продемонстрированы разрезанные на три части яблоки. От каждого яблока каждому ребенку отдается одна часть – так яблоки делятся на троих детей. Описывается, как решение данной задачи выглядит в математической записи. Каждая часть яблока представлена как 1/3, поэтому каждый ребенок получил 1/3 с каждого яблока, то есть 1/3+1/3=2/3. Так как оба яблока делили на три равные части, то таким образом образовалась дробь 2/3. Поэтому знак дроби может приниматься как знак деления, то есть записи 2/3 и 2:3 тождественны.
Далее рассматриваются особенности деления, которые приводят к тому, что в результате вычисления образуется дробь. В замечаниях указано, что с помощью дробей может быть записан результат деления любых натуральных чисел. В случае, когда деление выполняется нацело, частное является натуральным числом, а дробное число образуется, когда данные числа поделить нацело нельзя. Ниже правил деления демонстрируются примеры, помогающие усвоить материал. При делении 27 на 3 получается натурально число 9, поэтому результат деления может быть записан дробью, но также может записываться натуральным числом 27:3=27/3=9. При делении 3 на 1 результат может быть записан дробным числом 3/1, но в результате также получается натуральное число, поэтому моно записать 3:1=3/1=3. Если делить 5 на 6, то в результате не получается натуральное число, поэтому результат деления может быть представлен только в виде дроби 5:6=5/6. Аналогичный результат при делении 9 на 4 – его можно представить только в виде дроби 9:4=9/4.
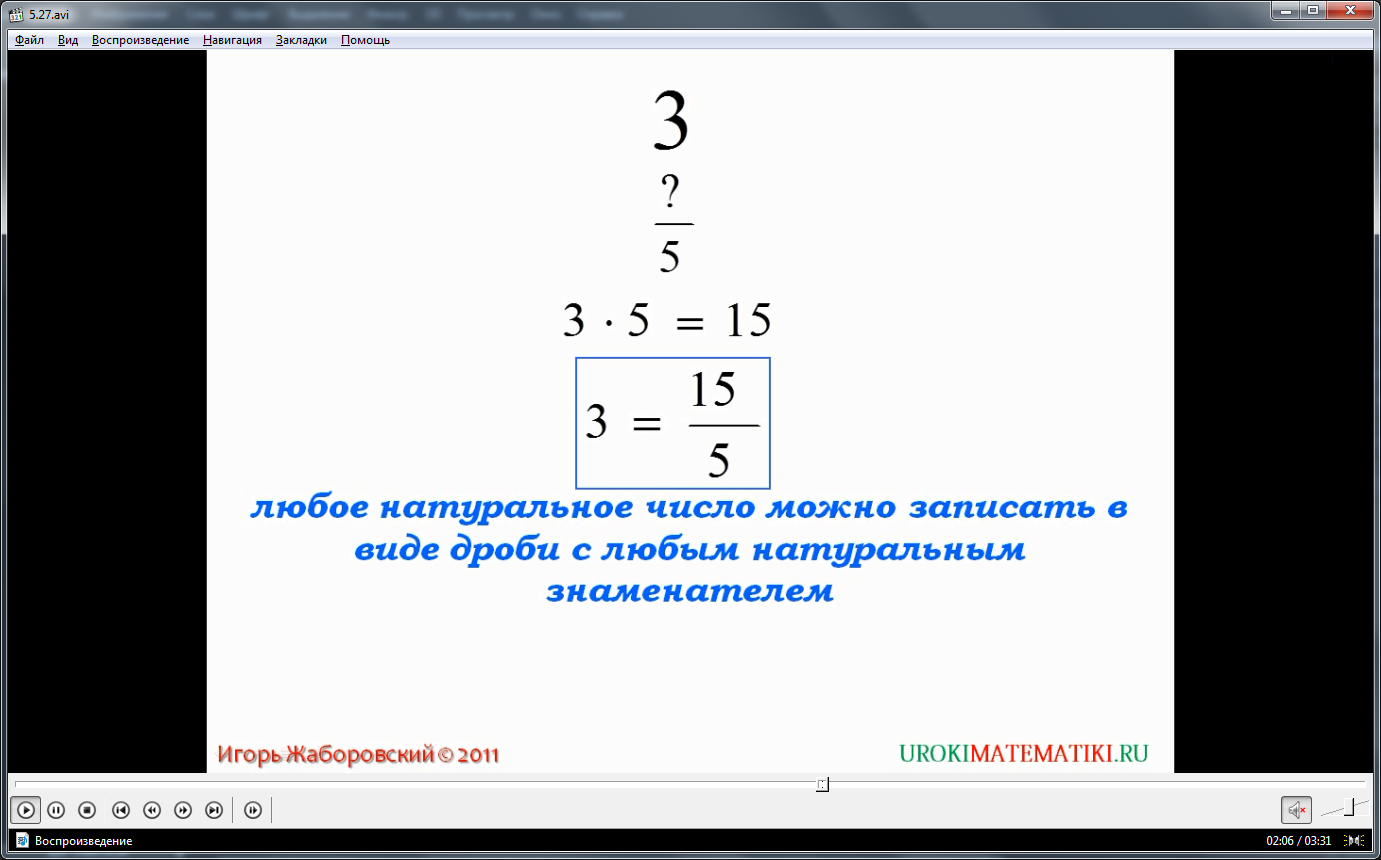
Утверждая, что каждое число может быть представлено в виде дроби, предлагается рассмотреть, как образуется дробь с произвольным знаменателем, представляющая некоторое число. Дается число 3, которое необходимо представить в виде дроби со знаменателем 5. В числителе данной дроби необходимо поставить число, которое при делении на 5 дало бы в результате 3. Таким числом является 3·5=15, так как при делении 15 на 5 получается 3. Поэтому дробь со знаменателем 5, представляющая число 3=15/5. Правило представления любого натурального числа в виде дроби в общем виде располагается ниже примера. В нем указывается, что всякое натуральное число может быть записано в виде дроби с указанным знаменателем. При этом числителем искомой дроби будет произведение знаменателя и данного числа. Правило выделено цветным шрифтом и рекомендовано к запоминанию.
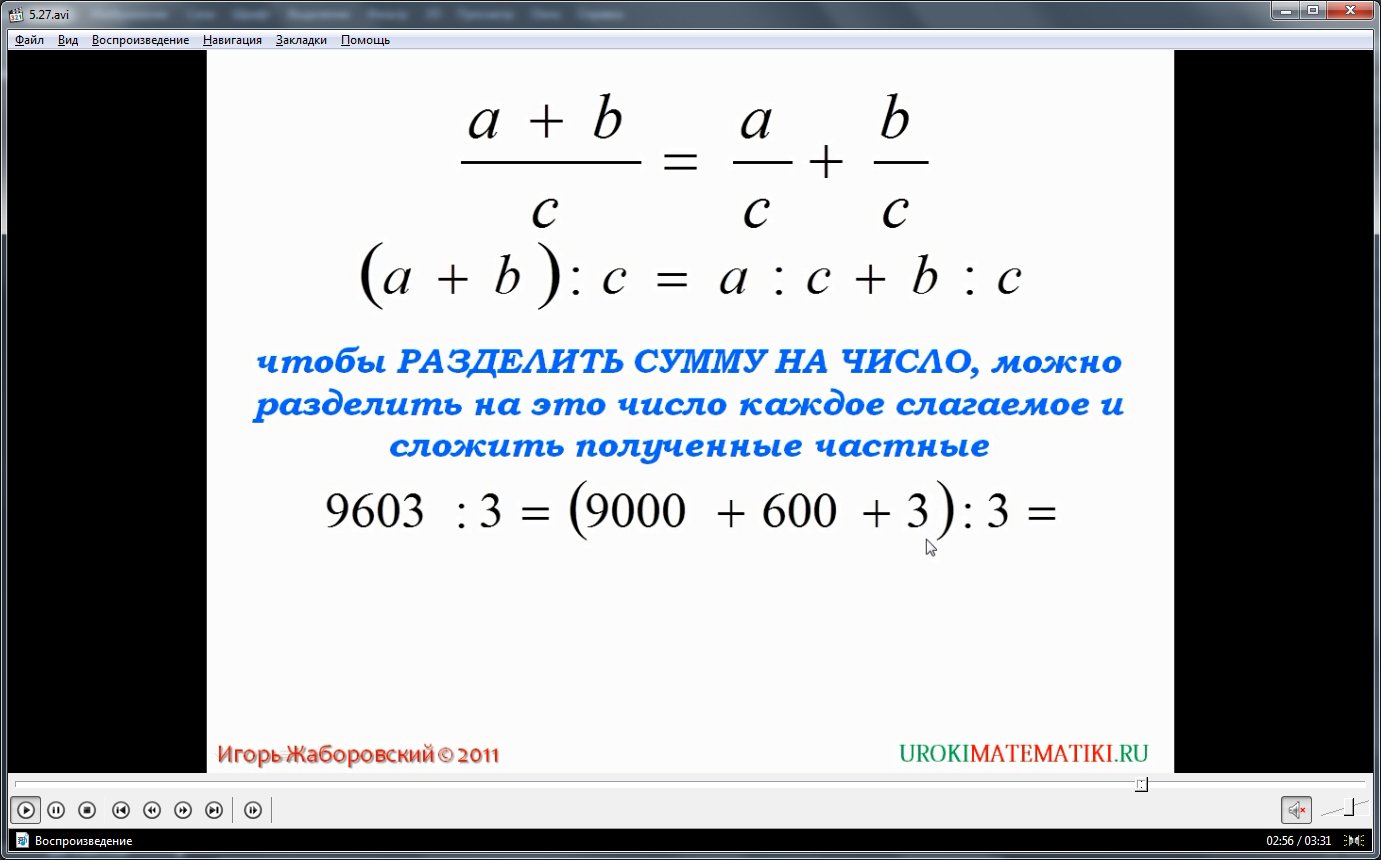
Ученикам напоминается правило сложения дробей с одинаковыми знаменателями (a+b)/c=a/c+b/c. В свете рассмотренных особенностей деления и связи его с понятием дроби, данное тождество может быть записано в виде (a+b):c=a:c+b:c. Иначе данное правило может быть описано словами, указывая, что для того чтобы разделить сумму на число, необходимо разделить на него каждое слагаемые, а затем полученные частные сложить. Правило подкрепляется примером, в котором оно используется 9603:3=(900+600+3):3. Зная, что для получения решения данного примера можно сначала найти частное от деления каждого слагаемого на делитель 3, а потом их сложить, раскладываем выражение на более простые задачи 9000:3+600:3+3:3. Затем складываем полученные частные 3000+200+1=3201.
Видеоурок заканчивается вопросами, на которые нужно будет ответить ученикам, чтобы проверить, как хорошо они поняли изучаемую тему. Им нужно будет вспомнить, каким числом будет частное, которое образуется от деления чисел нацело, а также какое число образуется, если деление нацело невозможно, уметь расписать в виде дроби натуральное число, сформулировать свойство деления суммы на число.
Видеоурок «Деление и дроби» рекомендуется использовать на школьном уроке математики для повышения эффективности обучения. Наглядность материала пригодится учителю, осуществляющему дистанционное обучение. Видео можно рекомендовать ученикам, которые требуют обучения на дому или недостаточно быстро усваивают материал, и им необходимы дополнительные занятия.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 7331 |
| Номер материала | 389 |