
Урок "Взаимно обратные числа"

Краткое описание документа:
Благодаря тому, что практически во всех современных школах есть необходимое оборудование, чтобы во время уроков демонстрировать детям видеозаписи и различные электронные обучающие ресурсы, появляется возможность лучше заинтересовать учеников в том, или ином предмете или в той, или иной теме. В результате повышается успеваемость учащихся и рейтинг школы в целом.
Ни для кого не секрет, что визуальная демонстрация во время урока помогает лучше запоминать и усваивать определения, задачи и теорию. Если это сопровождается и озвучиванием, то у ученика работают одновременно и зрительная, и слуховая память. Поэтому, видеоуроки считаются одними из наиболее эффективных материалов для обучения.
Есть ряд правил и требований, которым должны соответствовать видео-уроки, чтобы могли быть максимально эффективными и полезными для учеников соответствующего возраста. Фон и цвет текста должны быть выбраны соответствующим образом, размер шрифта должен быть не слишком мелким, чтобы текст могли читать и плохо видящие школьники, однако, и не слишком большим, чтобы раздражать зрение и создавать неудобства и т.п. Особое внимание уделяется и иллюстрациям, - они должны содержаться в меру и не отвлекать от основной темы.
Видеоурок «Взаимно обратные числа» является отличным примером подобного обучающего ресурса. Благодаря нему ученик 6 класса может полностью понять, что такое взаимно обратные числа, как их распознать и как с ними работать.
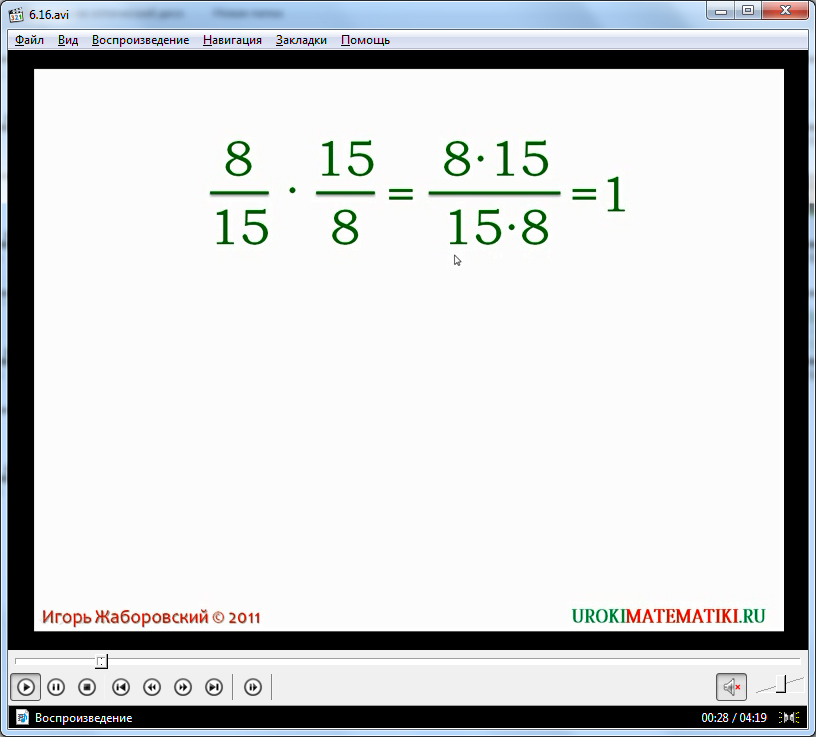
Урок начинается с простого примера, в котором две обыкновенные дроби 8/15 и 15/8 умножаются друг на друга. Появляется возможность вспомнить правило, по которому, как было изучено ранее, следует умножать дроби. То есть, в числителе следует записать произведение числителей, а в знаменателе – произведение знаменателей. В результате сокращения, что также стоит вспомнить, получается единица.
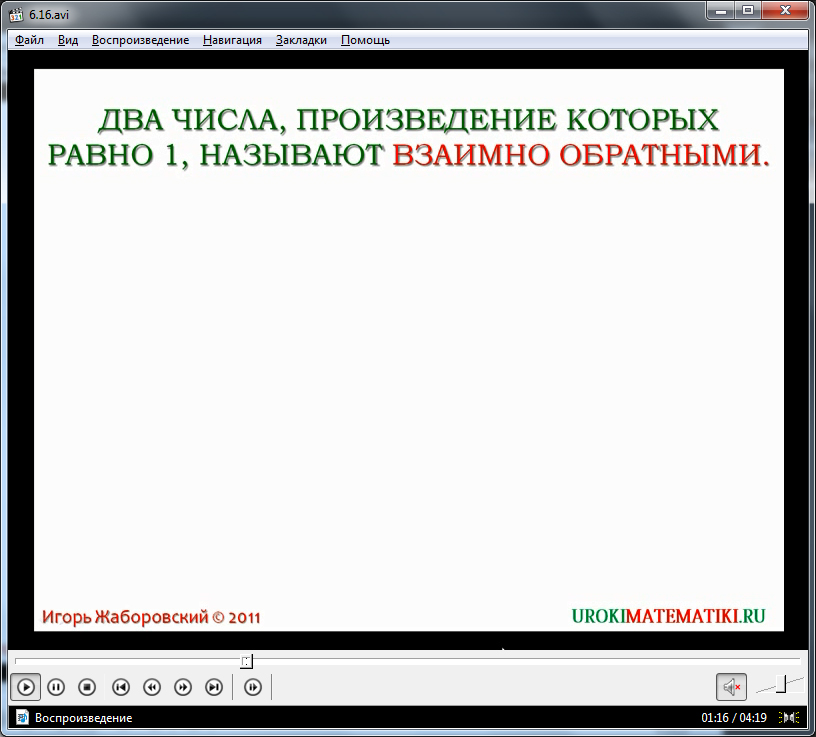
После данного примера, диктор дает обобщенное определение, которое выводится параллельно на экран. Оно гласит о том, что числа, которые при умножении друг на друга дают в результате единицу, называются взаимно обратными. Определение запоминается очень просто, однако оно закрепится более уверенно в памяти, если привести некоторые примеры.
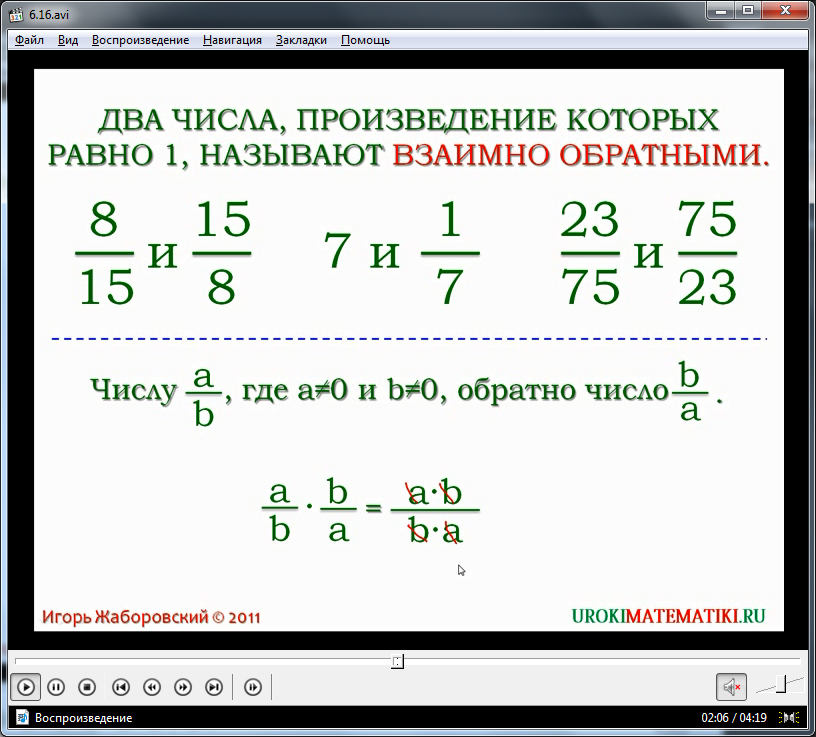
На экране после определения понятия взаимно обратных чисел выводится ряд произведений чисел, которые в результате выдают единицу.
Чтобы дать обобщенный пример, который не будет зависеть от определенных числовых значений, используются переменные a и b, которые отличны от 0. Почему? Ведь школьники в 6 классе должны прекрасно знать о том, что знаменатель любой дроби не может равняться нулю, а, чтобы показать взаимно обратные числа, не обойтись без расположения данных значений в знаменателе.
После вывода данной формулы и ее комментирования, диктор начинает рассматривать первое задание. Суть состоит в том, что необходимо найти обратное заданной смешанной дроби. Для его решения, дробь записывается в неправильном виде, и меняются местами числитель и знаменатель. Полученный результат и является ответом. Школьник может и самостоятельно его проверить, пользуясь определением взаимно обратных чисел.
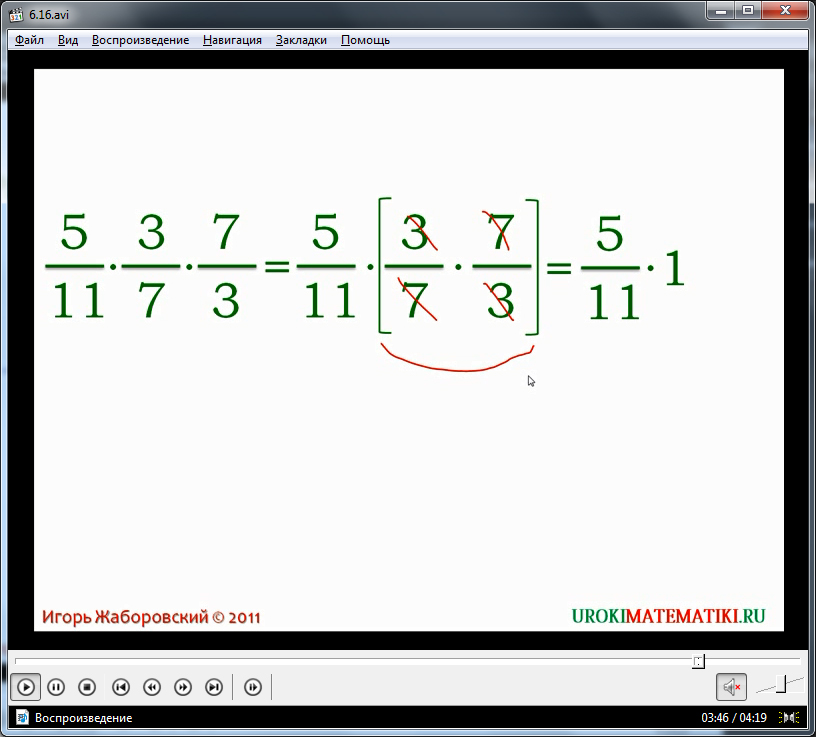
Видеоурок не ограничивается данным примером. Следом за предыдущим, на экран выводится еще одно задание, в котором необходимо найти произведение трех дробей. Если ученик проявит внимательность, то он обнаружит, что две из данных дробей являются обратными числами, следовательно, их произведение будет равняться единице. Опираясь свойством умножения, можно в первую очередь умножить взаимно обратные дроби, и в последнюю – умножить результат, т. е. 1, на первую дробь. Диктор подробно объясняет, пошагово демонстрируя на экране весь процесс от начала до конца. Напоследок дается теоретическое обобщенное объяснение свойству умножения, на которое опирались при решении примера.
Чтобы закрепить наверняка знания, стоит попытаться ответить на все вопросы, которые будут выведены в конце урока.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 5915 |
| Номер материала | 427 |