
Урок «Двугранный угол»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
В планиметрии основными объектами являются прямые, отрезки, лучи и точки. Лучи исходящие из одной точки, образуют одну их геометрических фигур–угол.
Мы знаем, что линейный угол измеряется в градусах и радианах.
В стереометрии к объектам добавляется плоскость. Фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости в геометрии называется двугранным углом. Полуплоскости – это грани двугранного угла. Прямая а – это ребро двугранного угла.
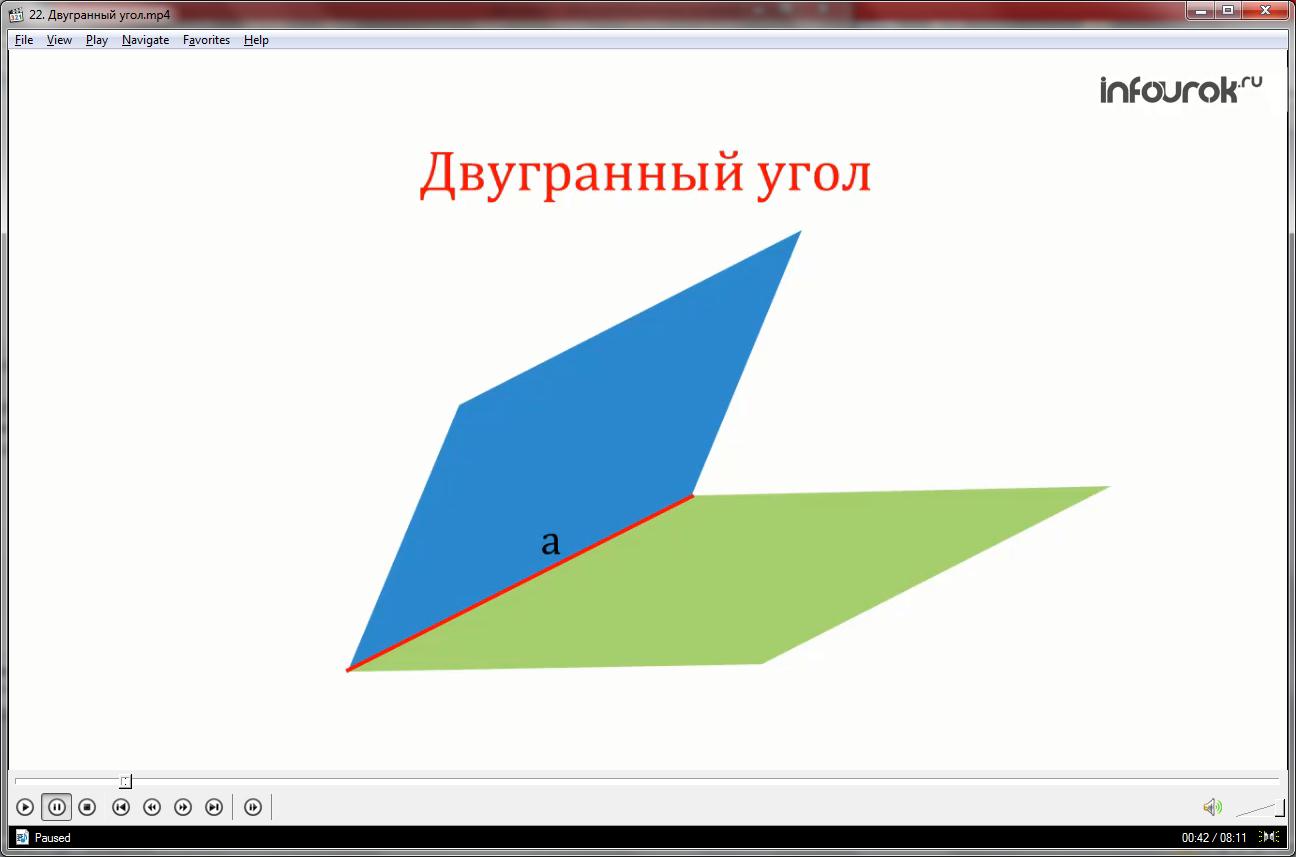
Двухгранный угол как и линейный угол можно назвать, измерить, построить. Это и предстоит нам выяснить в этом уроке.
Найдём двухгранный угол на модели тетраэдра АВСD.
Двугранный угол с ребром АВ называют CABD, где С и D точки принадлежащие разным граням угла а ребро АВ называют в середине
Вокруг нас достаточно много предметов с элементами в виде двухгранного угла.
Во многих городах в парках установлены специальные скамейки для примирения. Скамейка выполнена в виде двух сходящихся к центру наклонных плоскостей.
При строительстве домов часто используется так называемая двухскатная крыша. На этом доме крыша выполнена в виде двухгранного угла в 90 градусов.
Двугранный угол тоже измеряется в градусах или радианах, но как его измерить.
Интересно заметить, что крыши домов лежат на стропилах. А обрешётка стропил образует два ската крыши под заданным углом.
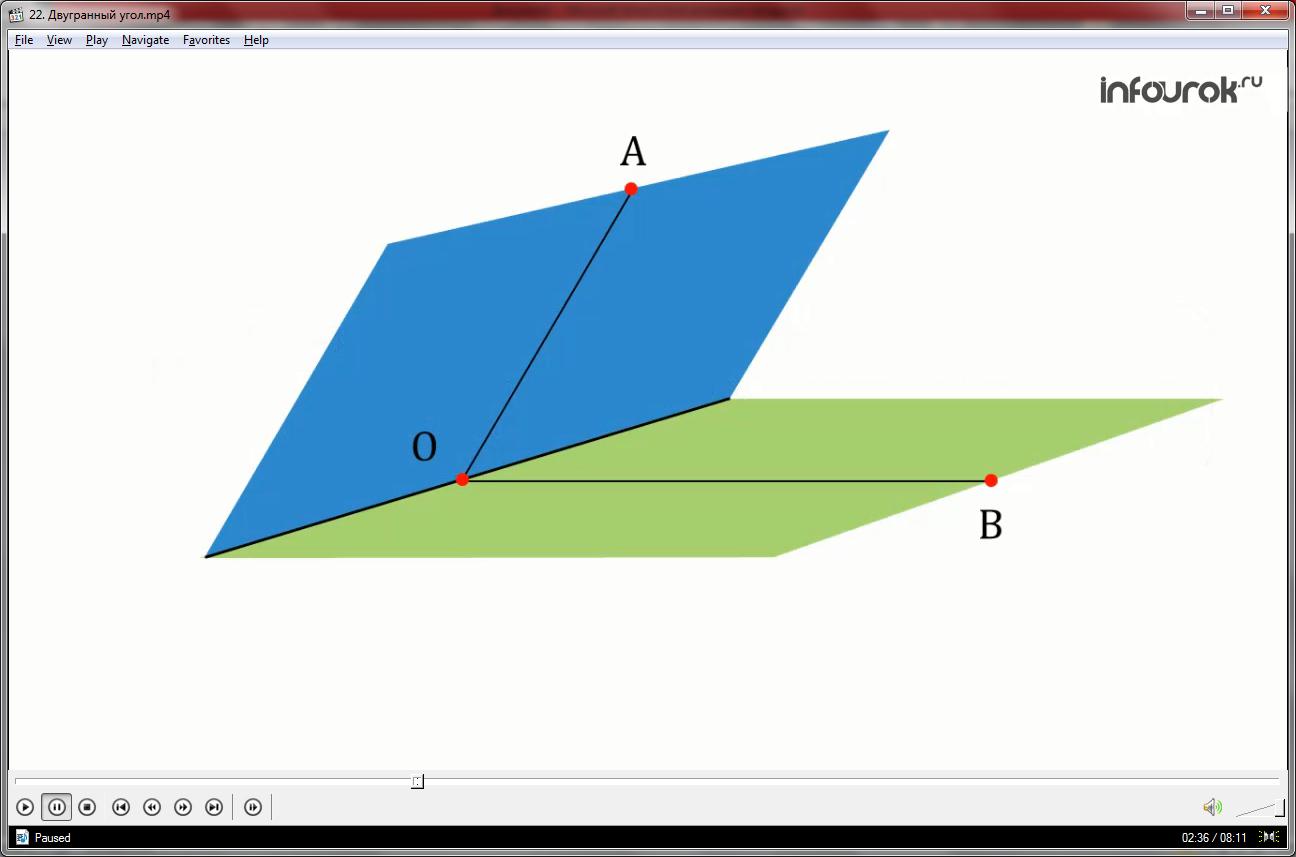
Перенесем изображение на чертёж. На чертеже для нахождения двухгранного угла на его ребре отмечается точка В. Из этой точки проводятся два луча ВА и ВС перпендикулярно ребру угла. Образованный этими лучами угол АВС называется линейным углом двугранного угла.
Градусная мера двугранного угла равна градусной мере его линейного угла.
Измерим угол АОВ.
Градусная мера данного двугранного угла равна шестидесяти градусам.
Линейных углов для двугранного угла можно провести бесконечное количество, важно знать, что все они равны.
Рассмотрим два линейных угла АОВ и А1О1В1 . Лучи ОА и О1А1 лежат в одной грани и перпендикулярны к прямой ОО1, поэтому они сонаправлены. Лучи ОВ и О1В1 так же сонаправлены. Поэтому угол АОВ равен углуА1О1В1 как углы с сонаправленными сторонами.
Так двугранный угол характеризуется линейным углом, а линейные углы бывают острые, тупые и прямые. Рассмотрим модели двугранных углов.
Тупой угол, если его линейный угол от 90 до 180 градусов.
Прямой угол, если его линейный угол равен 90 градусов.
Острый угол, елси его линейный угол от 0 до 90 градусов.
Докажем одно из важных свойств линейного угла.
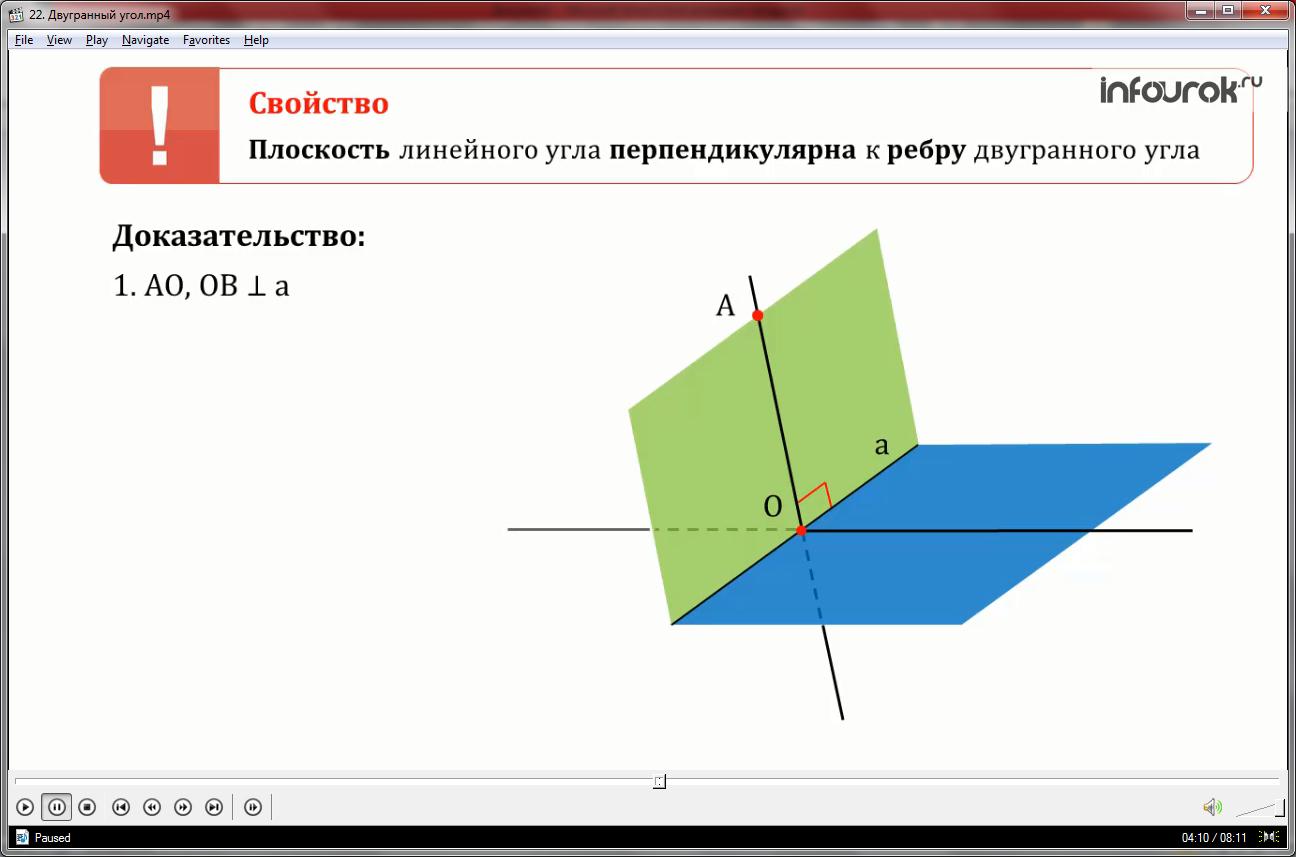
Плоскость линейного угла перпендикулярна к ребру двугранного угла.
Пусть угол АОВ – линейный угол данного двугранного угла. По построению лучи АО и ОВ перпендикулярные прямой а.
Через две пересекающиеся прямые АО и ОВ проходит плоскость АОВ по теореме: Через две пересекающиеся прямые проходит плоскость и притом только одна.
Прямая а перпендикулярна двум пересекающимся прямым лежащим в этой плоскости, значит по признаку перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости АОВ.
Для решения задач важно уметь строить линейный угол заданного двухгранного угла. Построить линейный угол двугранного угла с ребром АВ для тетраэдра АВСD.
Речь идет о двугранном угле, который образован, во-первых, ребром АВ, одной гранью АВD, второй гранью АВС.
Вот один из способов построения.
Проведем перпендикуляр из точки D к плоскости АВС, Отметим точку М основание перпендикуляра. Вспомним, что в тетраэдре основание перпендикуляра совпадает с центром вписанной окружности в основание тетраэдра.
Проведем наклонную из точки D перпендикулярно к ребру АВ, отметим точку N основание наклонной.
В треугольнике DMN отрезок NM будет проекций наклонной DN на плоскость АВС. По теореме о трёх перпендикулярах ребро АВ будет перпендикулярно проекции NМ.
Значит cтороны угла DNM перпендикулярны к ребру АВ, значит построенный угол DNM искомый линейный угол.
Рассмотрим пример решения задачи на вычисление двугранного угла.
Задача
Равнобедренный треугольник АВС и правильный треугольник АDB не лежат в одной плоскости. Отрезок CD является перпендикуляром к плоскости ADB. Найдите двугранный угол DABC, если AC=CB=2 см, АB= 4см.
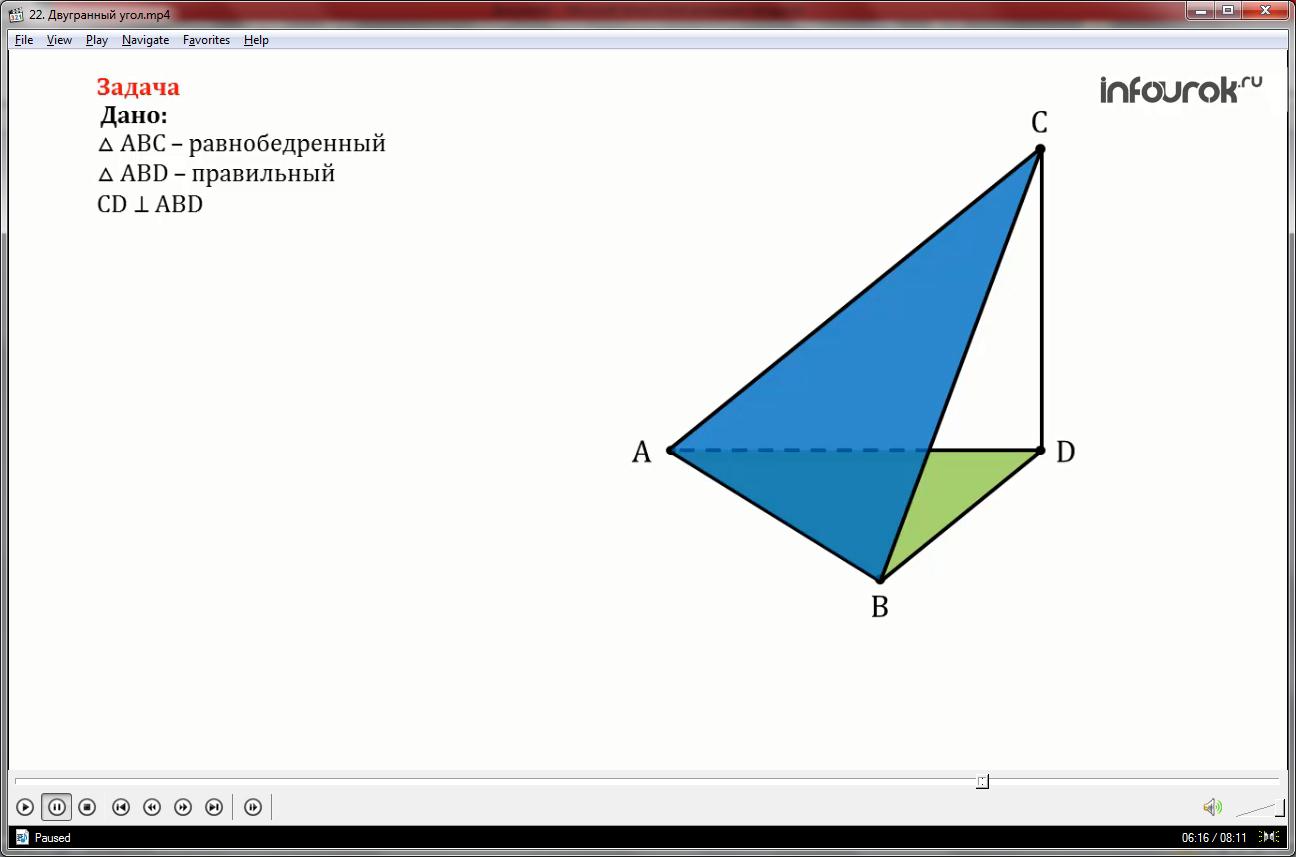
Двугранный угол DABC равен его линейному углу. Построим этот угол.
Проведем наклонную СМ перпендикулярно к ребру АВ, так как треугольник АСВ равнобедренный, то точка М совпадёт с серединой ребра АВ.
Прямая СD по условию перпендикулярна плоскости ADB, значит перпендикулярна прямой DM лежащей в этой плоскости. А отрезок МD является проекцией наклонной СМ на плоскость АDВ.
Прямая АВ перпендикулярна наклонной СМ по построению, значит по теореме о трех перпендикулярах перпендикулярна проекции MD.
Итак к ребру АВ найдены два перпендикуляра СМ и DМ. Значит они образуют линейный угол СMD двугранного угла DАВС. И нам останется его найти из прямоугольного треугольника СDM.
Так отрезок СМ медиана и высота равнобедренного треугольника АСВ, то по теореме Пифагора катет СМ равен 4 см.
Из прямоугольного треугольника DMB по теореме Пифагора катет DM равен двум корням из трёх.
Косинус угла из прямоугольного треугольника равен отношению прилежащего катета МD к гипотенузе СМ и равен три корня из трёх на два. Значит угол СМD равен 30 градусам.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 14527 |
| Номер материала | 936 |