
Урок "Функция y=ax^2+bx+c, её свойства и график"

Краткое описание документа:
Рассмотрим выражение вида ах2+вх+с, где а, в, с – действительные числа, а отлично от нуля. Это математическое выражение известно как квадратный трехчлен.
Напомним, что ах2 - это старший член этого квадратного трехчлена, а – его старший коэффициент.
Но не всегда у квадратного трехчлена присутствуют все три слагаемые. Возьмем для примера выражение 3х2 + 2х, где а=3, в=2, с=0.
Перейдем к квадратичной функции у=ах2+вх+с, где а, в, с – любые произвольные числа. Эта функция является квадратичной, так как содержит член второй степени, то есть х в квадрате.
Довольно легко построить график квадратичной функции, например, можно воспользоваться методом выделения полного квадрата.
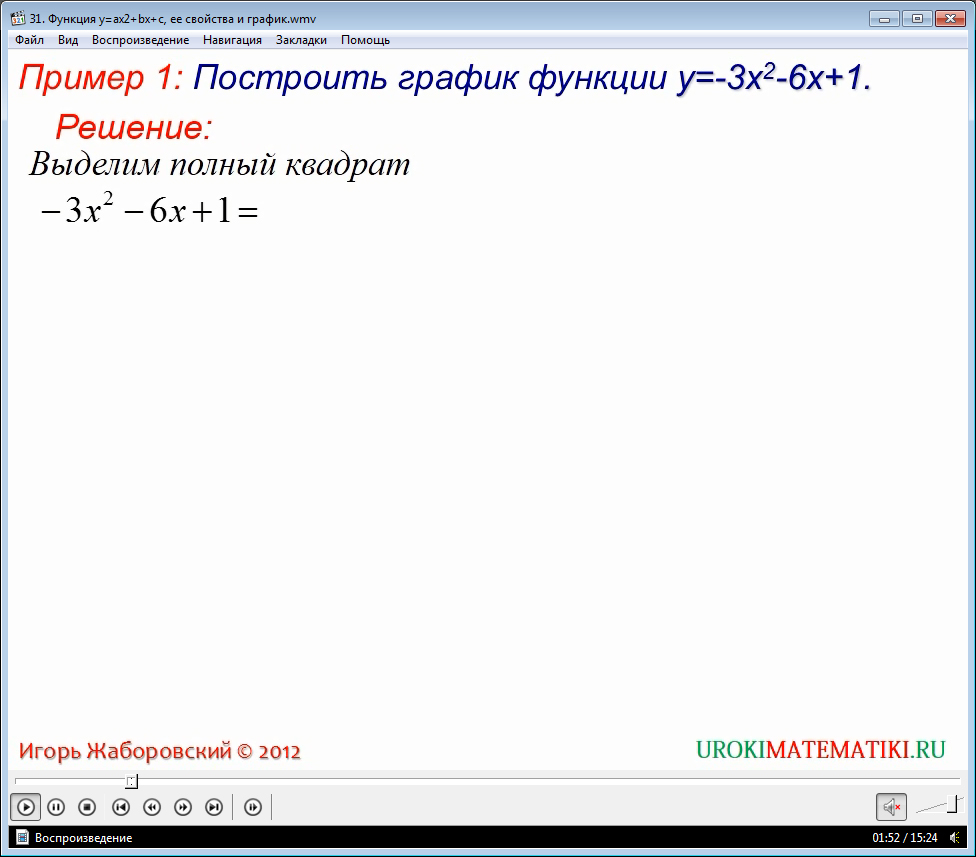
Рассмотрим пример построения графика функции у равно -3х2 – 6х + 1.
Для этого первое, что вспомним, схему выделения полного квадрата в трехчлене -3х2 – 6х + 1.
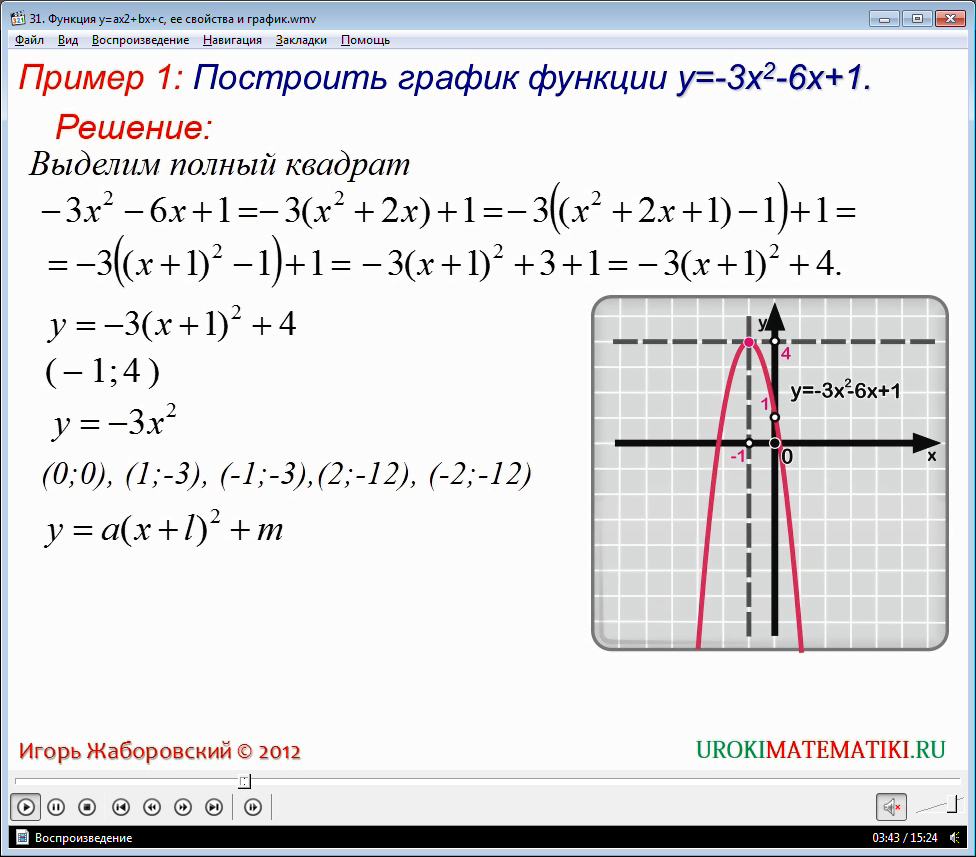
Вынесем -3 у первых двух слагаемых за скобки. Имеем -3 умножить на сумму х квадрат плюс 2х и прибавить 1. Добавив и отняв единицу в скобках, получаем формулу квадрата суммы, которую можно свернуть. Получим -3 умножить на сумму (х+1) в квадрате минус 1 прибавить 1. Раскрывая скобки и приводя подобные слагаемые, выходит выражение: -3 умноженное на квадрат суммы (х+1) прибавить 4.
Построим график полученной функции, перейдя к вспомогательной системе координат с началом в точке с координатами (-1; 4).
На рисунке из видео эта система обозначена пунктирными линиями. Привяжем функцию у равно -3х2 к построенной системе координат. Для удобства возьмем контрольные точки. Например, (0;0), (1;-3), (-1;-3), (2;-12), (-2;-12). При этом отложим их в построенной системе координат. Полученная при построении парабола является необходимым нам графиком. На рисунке это красная парабола.
Применяя метод выделения полного квадрата, мы имеем квадратичную функцию вида: у = а*(х+1)2 + m.
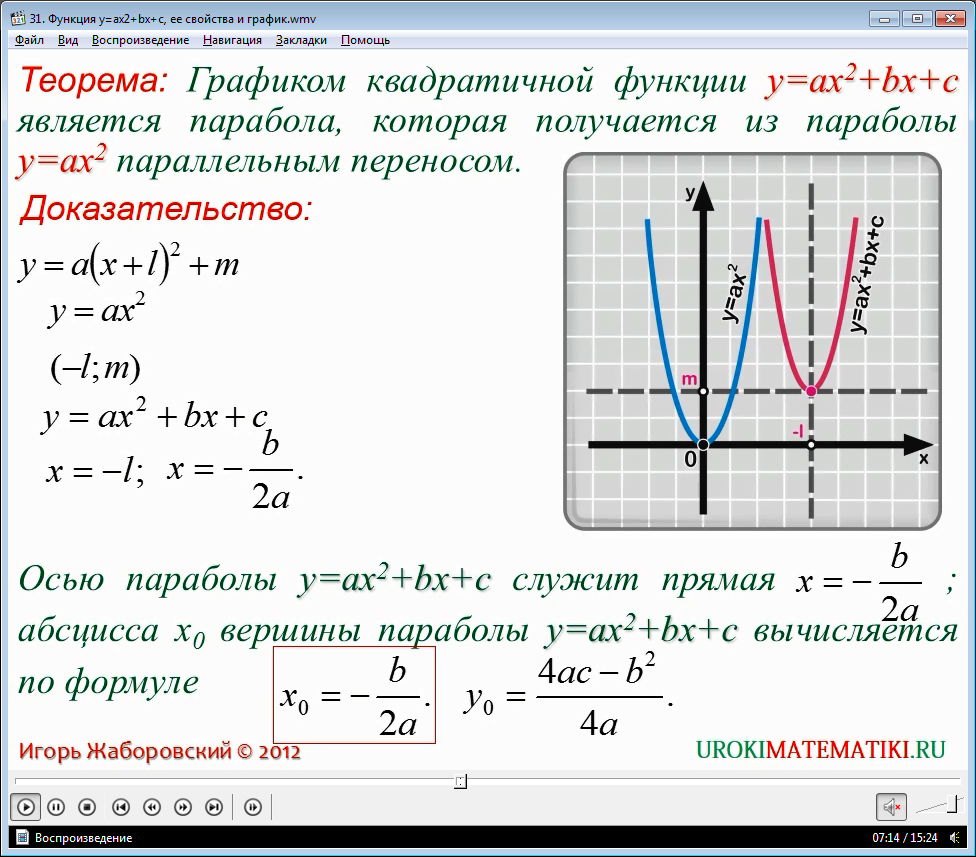
График параболы у = ах2 + bx + c легко получить из параболы у=ах2 параллельным переносом. Это подтверждено теоремой, которую можно доказать, выделив полный квадрат двучлена. Выражение ах2 + bx + c после последовательных преобразований превращается в выражение вида: а*(х+l)2+ m. Начертим график. Выполним параллельное перемещение параболы у = ах2, совмещая вершину с точкой с координатами (-l;m). Важно то, что х= -l, а значит –b/2а. Значит эта прямая является осью параболы ах2 + bx + c, ее вершина находится в точке с абсциссой х нулевое равно минус в, деленное на 2а, а ордината вычисляется по громоздкой формуле 4ас – b2 /. Но эту формулу запоминать не обязательно. Так как, подставив значение абсциссы в функцию, получим ординату.
Для определения уравнения оси, направления ее ветвей и координат вершины параболы, рассмотрим следующий пример.
Возьмем функцию у = -3х2 - 6х + 1. Составив уравнение оси параболы, имеем, что х=-1. А это значение является координатой х вершины параболы. Осталось найти только ординату. Подставив значение -1 в функцию, получим 4. Вершина параболы находится в точке (-1; 4).
График функции у = -3х2 - 6х + 1 получен при параллельном переносе графика функции у = -3х2, значит, и ведет себя аналогично. Старший коэффициент отрицателен, поэтому ветви направлены вниз.
Мы видим, что для любой функции вида y = ах2 + bx + c, самым легким является последний вопрос, то есть направление веток параболы. Если коэффициент а положительный, то ветви - вверх, а если отрицательный, то - вниз.
Следующим по сложности идет первый вопрос, потому что требует дополнительных вычислений.
И самый сложный второй, так как, кроме вычислений, еще необходимы знания формул, по которым находятся х нулевое и у нулевое.
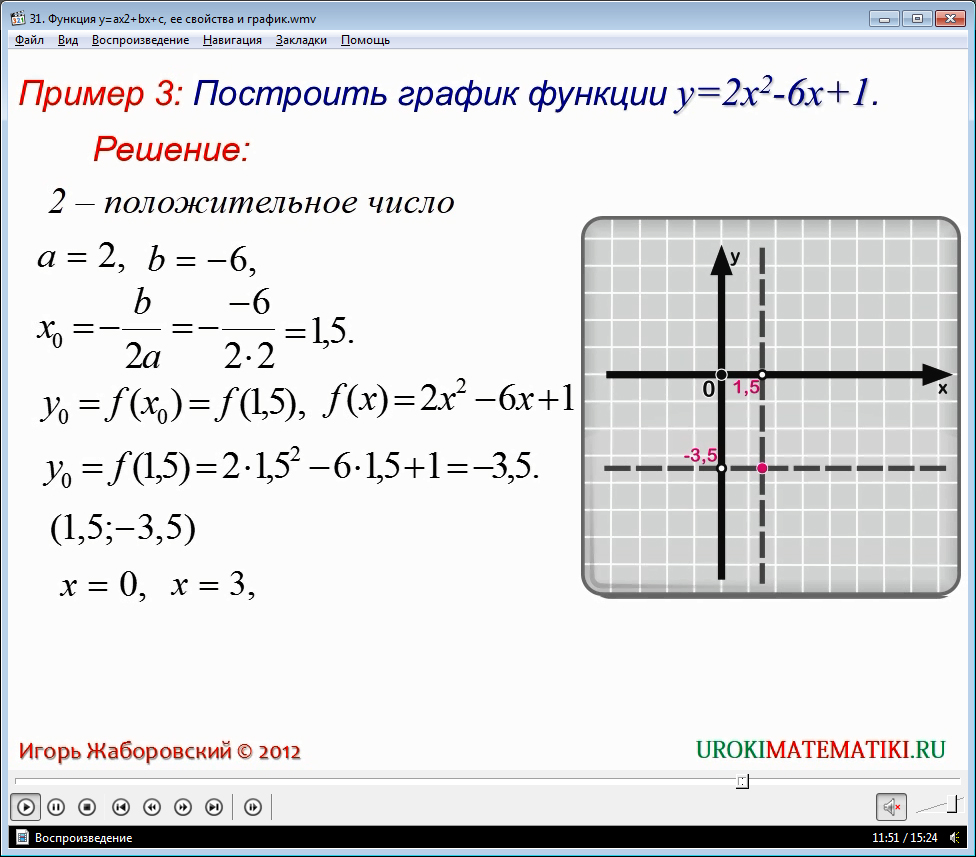
Построим график функции у = 2х2 - х + 1.
Определяем сразу - графиком является парабола, ветви направлены вверх, так как старший коэффициент равен 2, а это положительное число. По формуле находим абсциссу х нулевое, она равна 1,5. Для нахождения ординаты вспомним, что у нулевое равно функции от 1,5, при вычислении получим -3,5.
Вершина – (1,5;-3,5). Ось – х=1,5. Возьмем точки х=0 и х=3. у=1. Отметим данные точки. По трем известным точкам строим искомый график.
Для построения графика функции ах2 + bx + c необходимо:
- найти координаты вершины параболы и отметить их на рисунке, потом провести ось параболы;
- на оси ох взять две симметричные, относительно оси, параболы точки, найти значение функции в этих точках и отметить их на координатной плоскости;
- через три точки построить параболу, при необходимости можно взять еще несколько точек и строить график по ним.
В следующем примере мы научимся находить наибольшее и наименьшее значения функции -2х2 + 8х - 5 на отрезке [0;3].
По алгоритму: а=-2, в=8, значит х нулевое равно 2, а у нулевое – 3, (2;3) – вершина параболы, а х=2 является осью.
Возьмем значения х=0 и х=4 и найдем ординаты этих точек. Это -5. Строим параболу и определяем, что наименьшее значение функции -5 при х=0, а наибольшее 3, при х=2.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 38083 |
| Номер материала | 554 |