
Урок "Свойства функции y=kx^2 при k меньше 0"

Краткое описание документа:
Разобраться в описании свойств функции y = kx2 при k < 0 поможет уже известная вам геометрическая модель – парабола.
В видеоуроке вы сможете детально ознакомиться с основными свойствами и иллюстрациями, которые способствуют лучшему усвоению материала. Итак, рассмотрим некоторые из них.
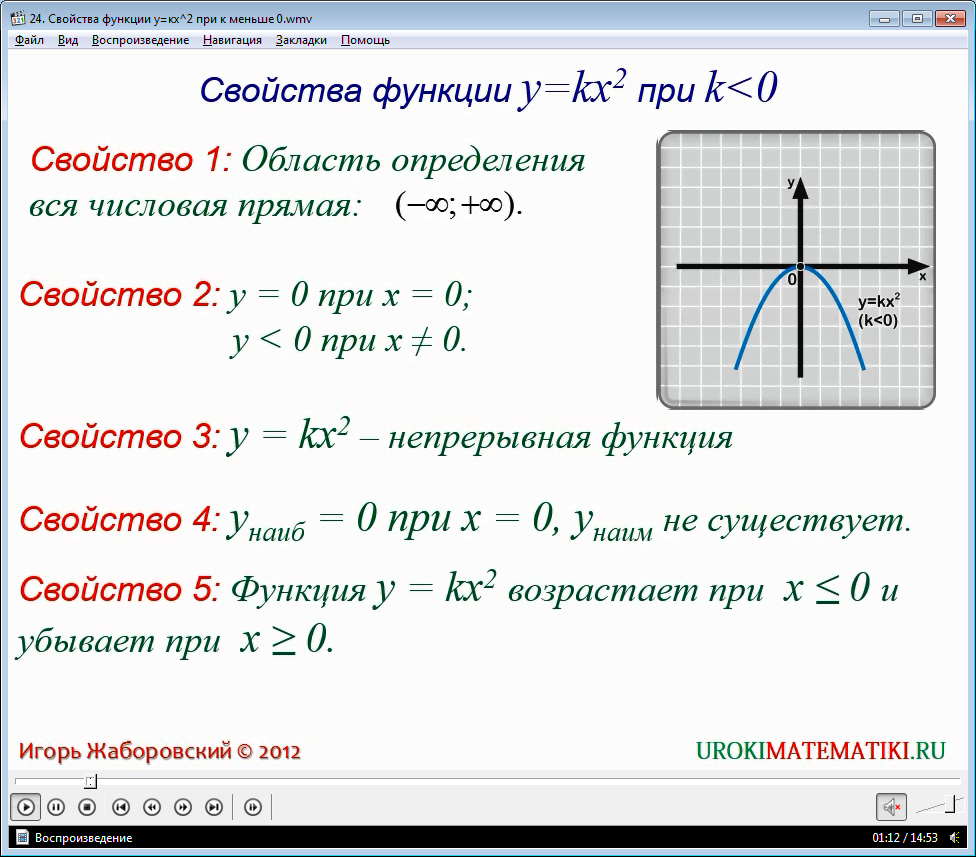
При любом значении x функция y = kx2 определена в любой точке. В математике это принято обозначать так: D(f) = (-∞;∞)- область определения функции (-∞;∞), то есть абсолютно вся координатная прямая.
При x = 0 => y = 0, а при х не равен 0 => y < 0.
y = kx2 - это непрерывная функция. Раньше вы уже встречались с этим термином, но в немного в иной формулировке. В видеоуроке дано пояснение этого пункта.
При x = 0 достигается yнаиб = 0, а унаим не существует.
При x < 0 функция y = kx2 возрастает, а при x > 0 убывает.
Функция y = kx2 при k < 0 не ограничена снизу, но ограничена сверху. Это значит, что область значений функции: E(f) = (-∞;0].
С детальным пояснением последнего свойства вы можете ознакомиться в видеоуроке.
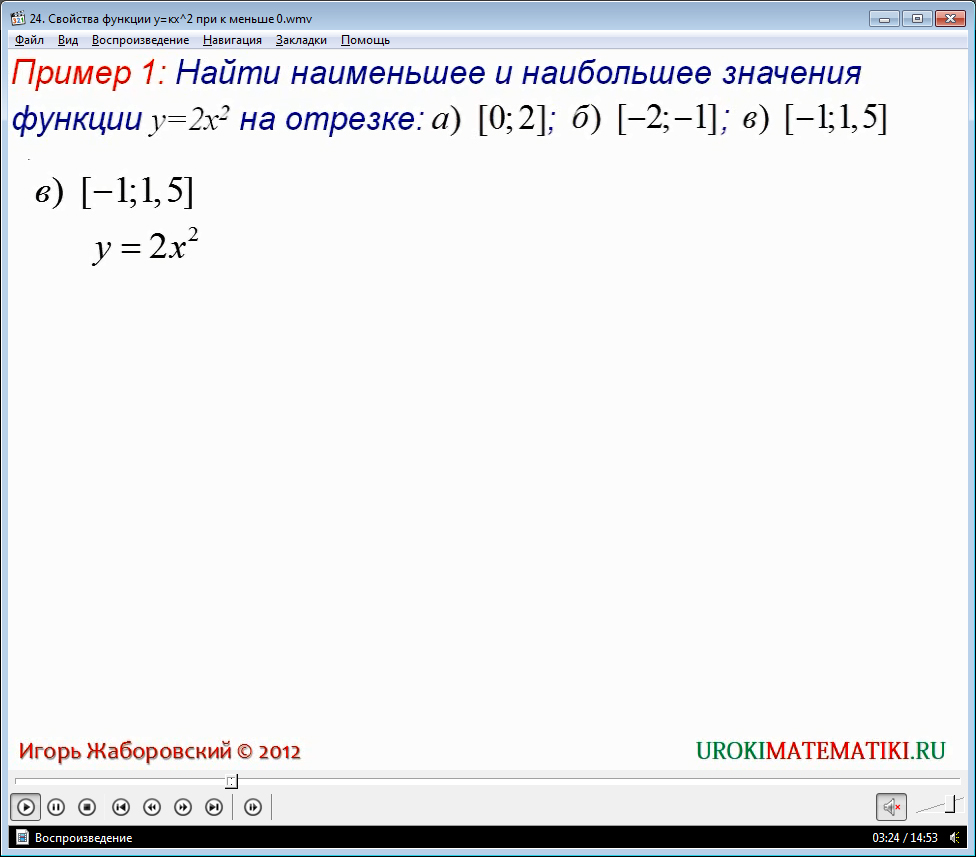
Рассмотрим пример. Найти наибольшее и наименьшее значение функции
y = - (x2/2) + 2x + 8/(x – 2) + 5 на отрезке [-2;1].
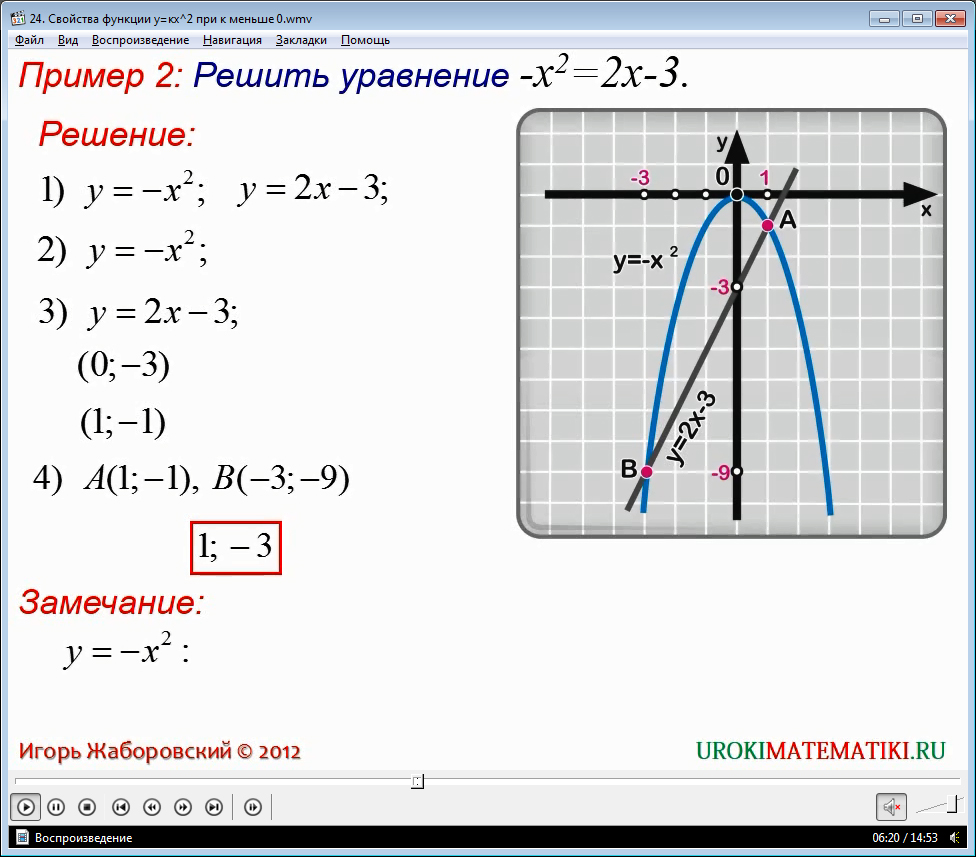
Найдем производную данной функции: y’ = -x + 2 – 8/(x – 2)2.
В стационарных точкахy; = 0, поэтому = -(х + 2) – 8/(х – 2)2 = 0.
Отсюда – 8/(х – 2)3 = 1 или (х – 2)3 = -8; х – 2 = -2 => x = 0.
Найдем значение функции.
y(-2) = -4/2 – 4 + 8/(-2 - 2) + 5 = -2 – 4 – 2 + 5 = -3.
y(0) = -0 + 0 + 8/(-2) + 5 = -4 + 5 = 1.
y(1) = -1/2 + 2 + 8/(1 – 2) + 5 = -1,5.
Следовательно, наибольшее значение достигается в точке x = 0, yнаиб = y(0) = 1.
Наименьшее значение достигается в точке х = -2, унаим = у(-2) = -3.
С другими примерами и способами их решения вы можете ознакомиться, посмотрев видеоурок.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9552 |
| Номер материала | 547 |