
Урок «Компланарные вектора»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости.
Иначе:
векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
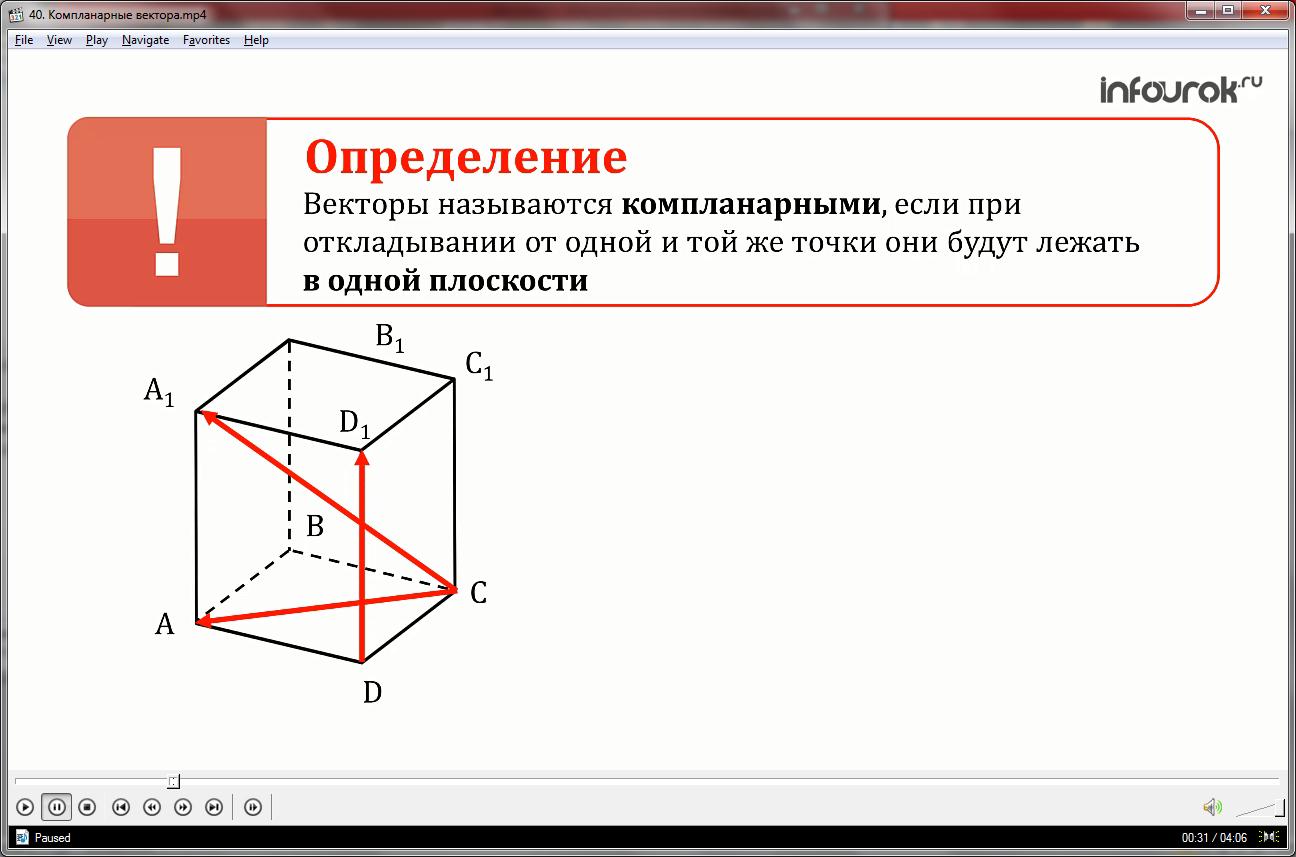
На рисунке векторы CA,CA1,DD1 компланарны, так как, если отложить от точки C вектор CC1=DD1 то все три вектора CA, CA1,CC1 и окажутся лежащими в одной плоскости. Векторы DC,CA,DD1 не компланарны, так как вектор DD1 не лежит в плоскости ACD.
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны. Три произвольных вектора могут быть как компланарными, так и некомпланарными.
Докажем признак компланарности трех векторов. Если вектор можно представить в виде =x , где х и у – некоторые числа, то векторы – компланарны.
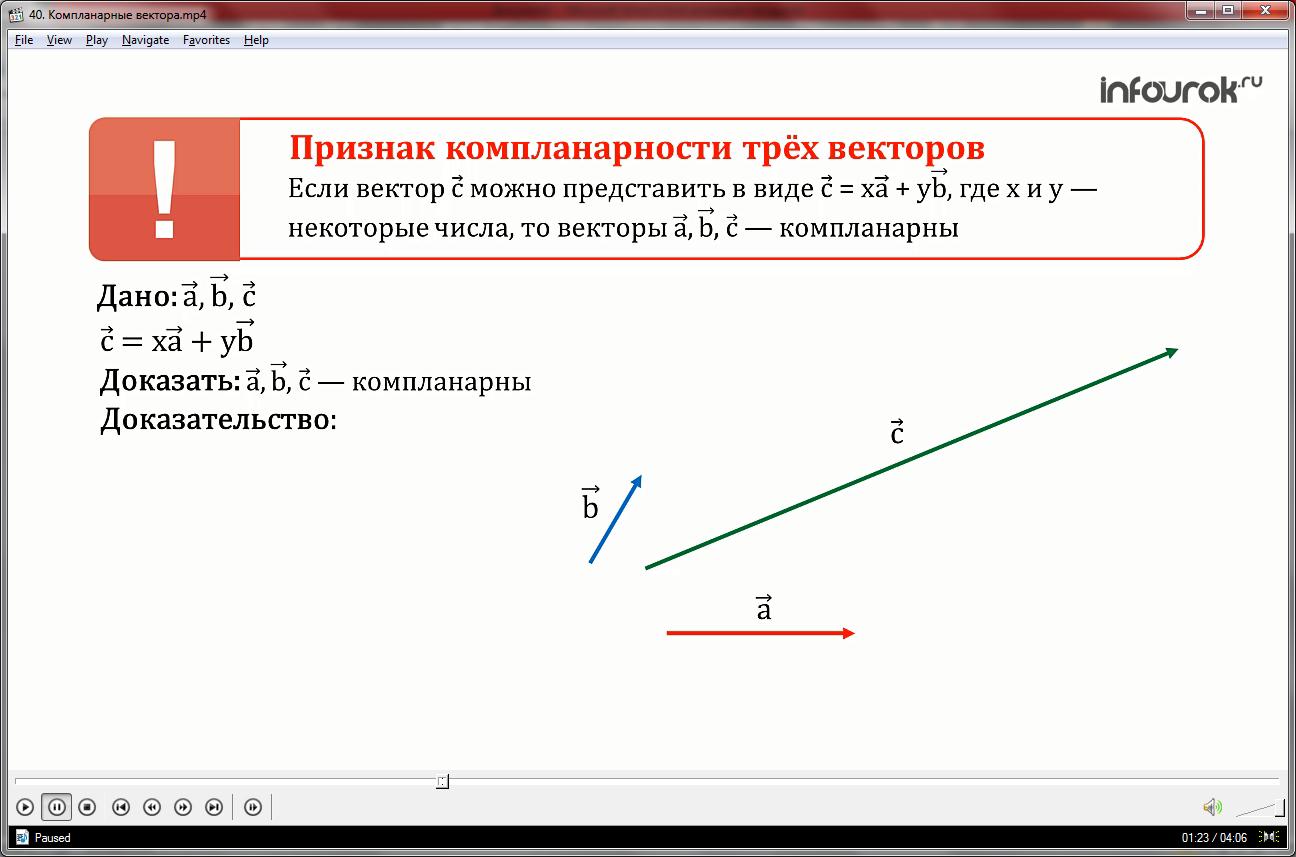
Для доказательства будем считать, что векторы а и в неколлинеарны, так как если они коллинеарны, то компланарность очевидна. Отложим от произвольной точки О векторы ОА и ОВ, равные соответственно векторам данным а и в. Вектороы ОА и ОВ лежат в одной плоскости ОАВ. Вектор ОА1 равен вектору ОА, умноженному на число х. Вектор ОВ1 равен вектору ОВ, умноженному на число у. Векторы ОА1 и ОВ1 так же лежат в этой плоскости. Следовательно, их сумма тоже лежит в этой плоскости. А их сумма равна вектору с. Значит , и вектор с лежит в этой плоскости. Векторы а, в и с компланарны. Что и требовалось доказать.
Справедливо и утверждение, обратное признаку компланарности векторов:

Если векторы а, в, с компланарны, а векторы а и в неколлинеарны, то вектор с можно представить как сумму x , при чем коэффициенты х и у определяются единственным образом.
В таком случае говорят, что вектор с разложен по векторам а и в.
Рассмотрим задачу №355(а) Дан параллелепипед АВСDA1B1C1D1.
Компланарны ли векторы АА1, СС1, ВВ1?
Решение : Три вектора, среди которых имеются два коллинеарных, компланарны. А в нашем случае все три вектора являются коллинеарными так как лежат на параллельных ребрах параллелепипеда, значит, эти векторы компланарны.
Рассмотрим задачу

Дан параллелепипед АВСDA1B1C1D1.
Компланарны ли векторы АD, СС1, А1В1?
Решение: Вектор АА1 равен вектору СС1, вектор АВ равен А1В1. Векторы АВ, АD и АА1 не компланарны, так как вектор АА1 не лежит в плоскости АВС. Значит, и АD, СС1, А1В1- некомпланарны.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 16373 |
| Номер материала | 954 |