
Урок «Многогранники. Понятие правильного многогранника»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сегодня мы продолжаем изучение многогранников. На прошлом занятии вы познакомились с понятием симметрии и её элементами.
Вспомним, симметрию относительно точки(центра) называют центральной;
симметрию относительно прямой(оси)-осевой;
симметрию относительно плоскости называют зеркальной.
Вы уже знаете, что многоугольник называется правильным, если все его углы равны и все его стороны равны.
А какой многогранник называется правильным?
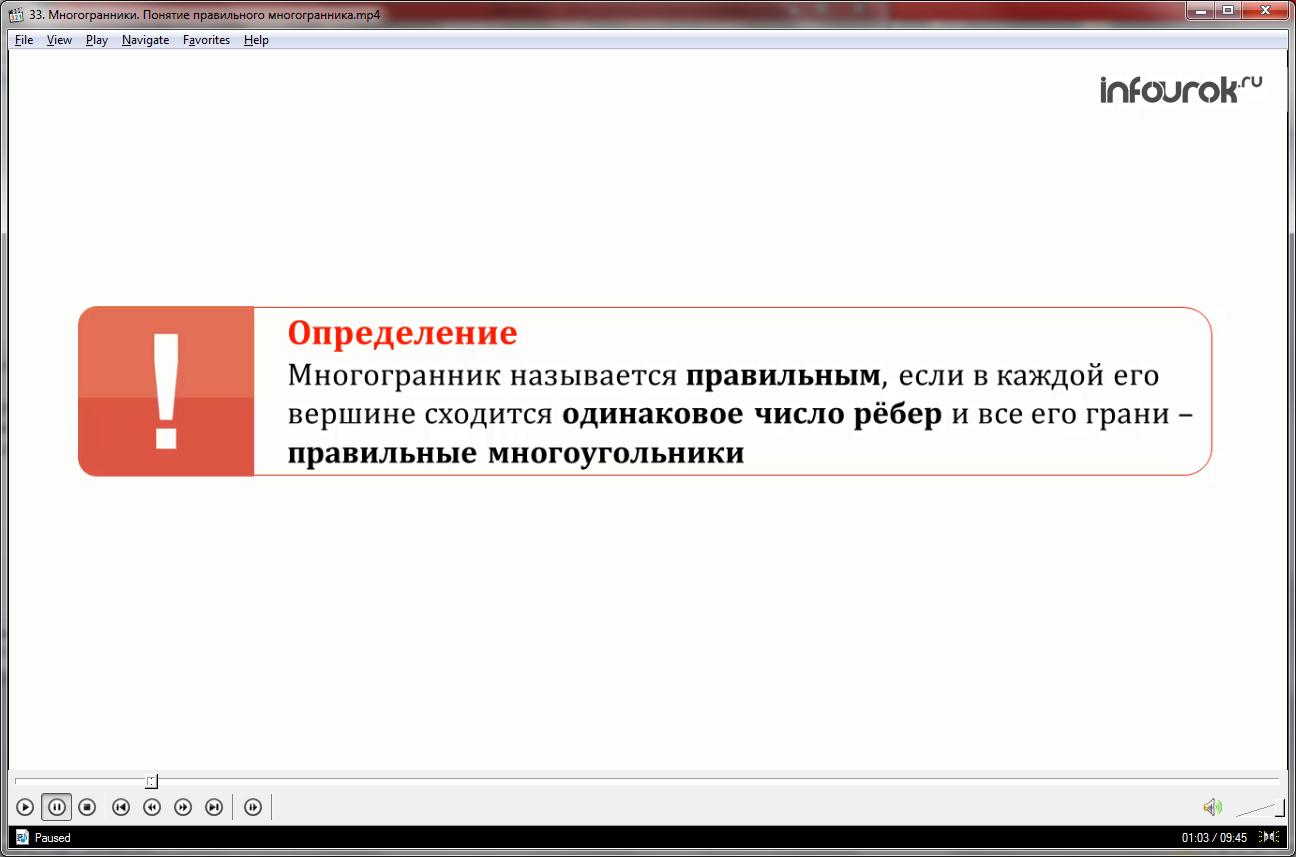
Многогранник называется правильным, если в каждой его вершине сходится одинаковое число рёбер и все его грани- правильные многоугольники.
Одним из примеров правильного многогранника является куб, так как все его грани-равные квадраты, а к каждой вершине сходится три ребра.
Очевидно, что в правильном многограннике равны все двугранные углы, содержащие две грани с общим ребром, а также все грани равны.
Попробуем доказать, что не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.
Доказательство.
1.Пусть при одной вершине правильного многогранника сходится n рёбер, тогда плоских углов при этой вершине будет тоже n, причём эти углы равны между собой.
2. Пусть один из этих углов равен α, тогда сумма плоских углов при вершине равна n*α и по свойству плоских углов многогранного угла мы получим n*α<3600, откуда найдём альфа: α<
3.Известно, что угол правильного n-угольника равен
β= . Начиная с n=7 плоский угол станет меньше 600, а такого правильного многоугольника не существует.
Таким образом, мы доказали, что не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.
Рассмотрим виды правильных многогранников:
1. Грани правильного многогранника- правильные треугольники, тогда β=600
а) 600*3=1800<3600. В этом случае правильный многогранник имеет 4 грани и называется правильным тетраэдром.
Правильный тетраэдр составлен из четырёх равносторонних треугольников
б) 600*4=2400<3600. В этом случае правильный многогранник имеет 8 граней и называется правильным октаэдром. Правильный октаэдр составлен из восьми равносторонних треугольников.
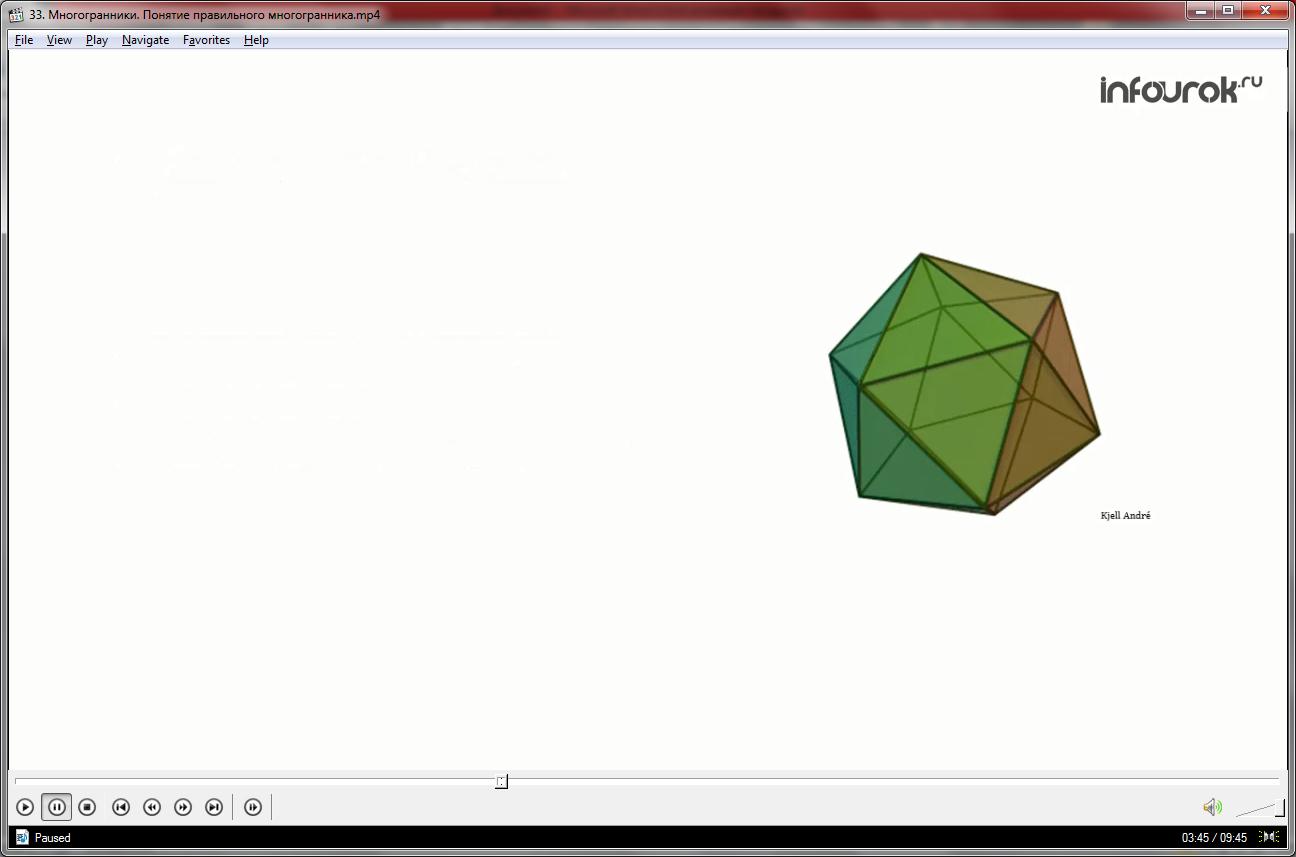
в) 600*5=3000<3600. В этом случае правильный многогранник имеет 20 граней и называется правильным икосаэдром. Правильный икосаэдр составлен из двадцати равносторонних треугольников
г) 600*6=3600-это противоречит свойству о сумме плоских углов многогранного угла. Значит, других правильных многогранников, грани которых- правильные треугольники не, существует.
2) Грани правильного многогранника- правильные четырёхугольники(квадраты), тогда β=900
а) 900*3=2700<3600. В этом случае правильный многогранник имеет 6 граней и называется правильным гексаэдром(кубом).
б) 900*4=3600, следовательно, больше других правильных многогранников, грани которых квадраты не существует.
3) Грани правильного многогранника -правильные пятиугольники, β=1080
а) 1080*3=3240<3600. В этом случае правильный многогранник имеет 12 граней и называется правильным додекаэдром.
Правильный додекаэдр составлен из двенадцати правильных пятиугольников.
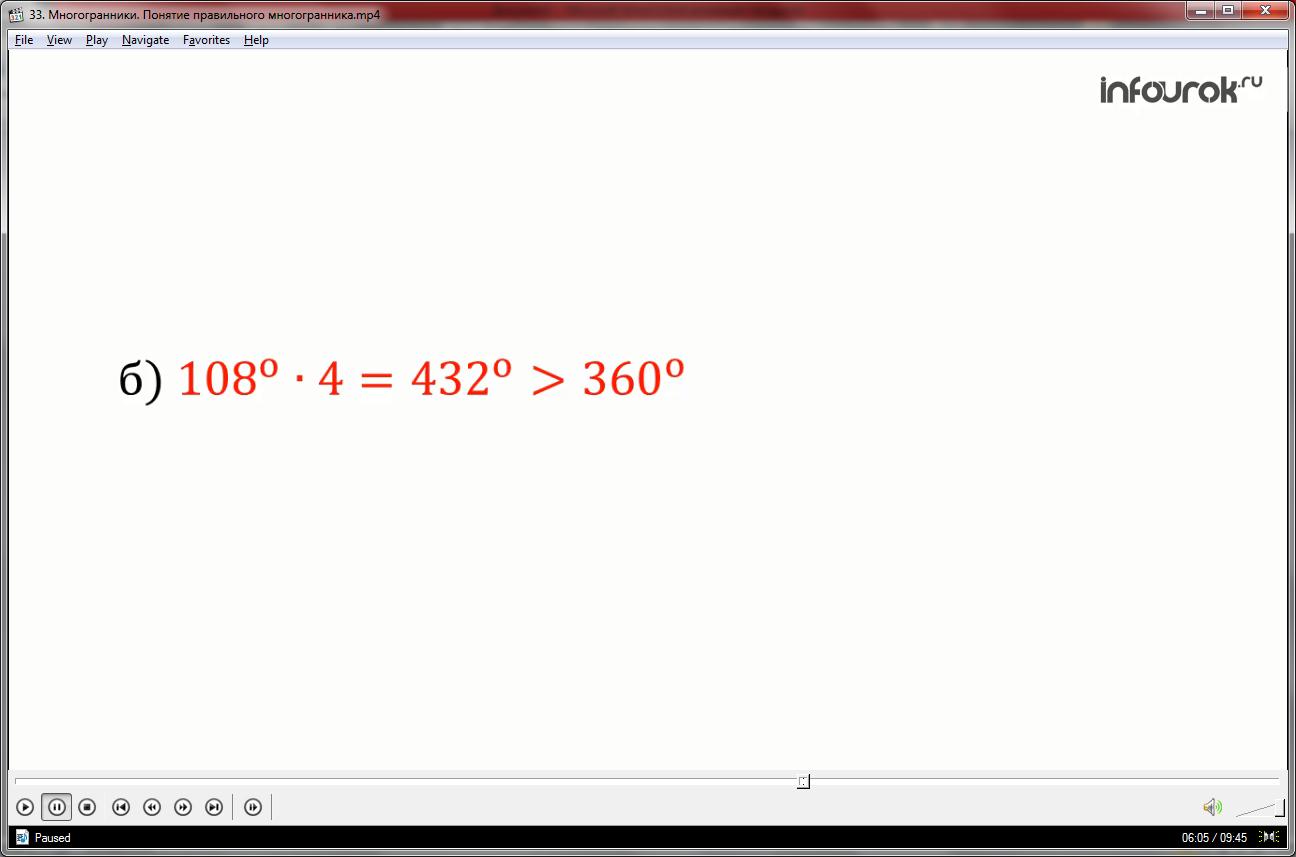
б) 1080*4=4320>3600, значит, других правильных многогранников, грани которых правильные пятиугольники, не существует.
Таким образом, мы убедились, что каждая вершина правильного многогранника может быть вершиной или трёх, четырёх или пяти равносторонних треугольников; или трёх квадратов или трёх правильных пятиугольников.
Поэтому других видов правильных многогранников кроме тетраэдра, октаэдра, куба (гексаэдра), икосаэдра и додекаэдра не существует.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела»
Разберём несколько задач, применяя полученные знания.
Задача 1.
Найти угол между двумя диагоналями граней куба, имеющими общий конец.
Решение:
1. Пусть а-это ребро куба.
Вы уже знаете, что все грани куба- это равные квадраты.
Предположим длинна ребра куба равна а и по теореме Пифагора: из треугольника АА1В можем вычислить диагональ каждой грани куба, тогда получаем :
A1В= A1C1=ВС1= = =а
2. Поскольку A1В= A1C1=ВС1, можно сделать вывод, что треугольник A1C1В-равносторонний, все углы которого равны 60 градусов.
Итак, угол между двумя диагоналями граней куба, имеющими общий конец, равен 60 градусов.
Задача 2
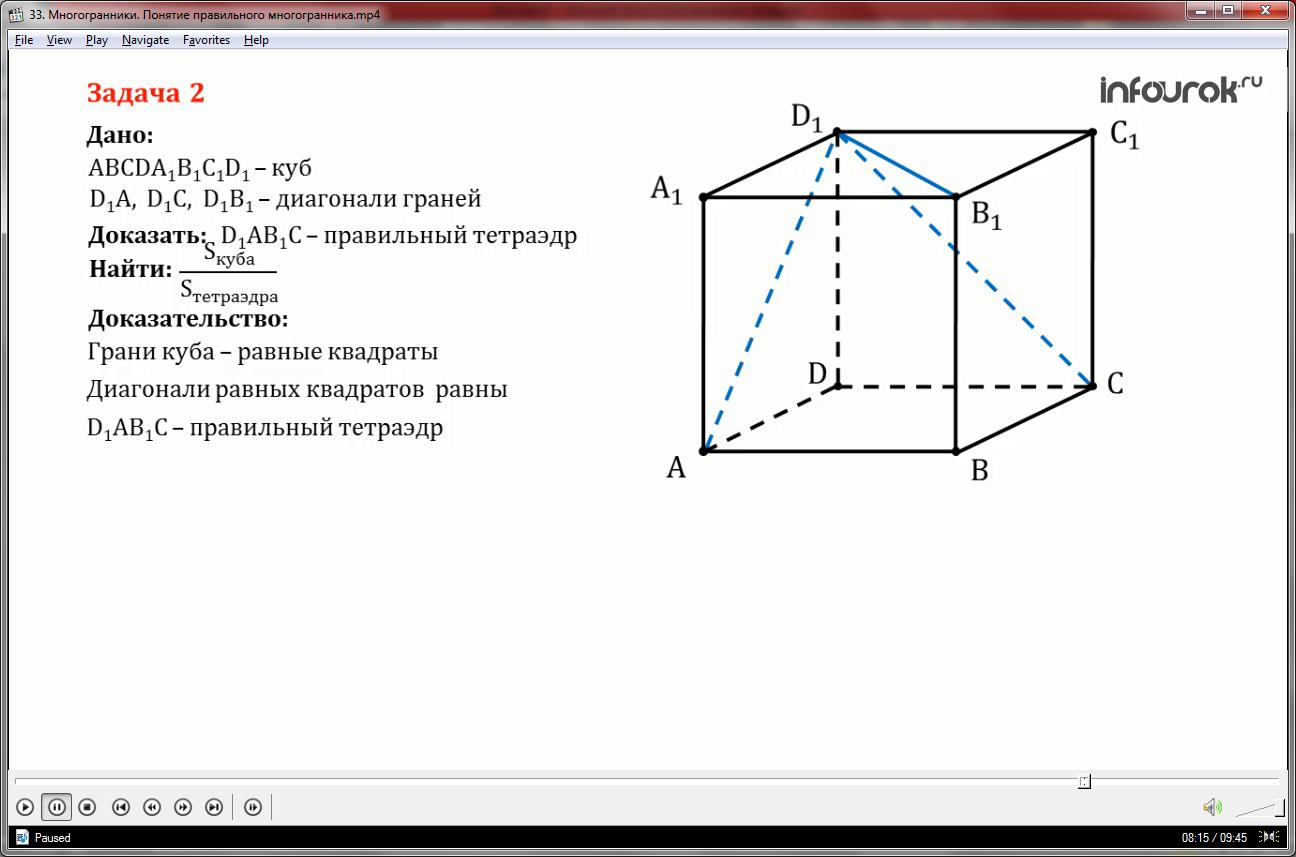
В кубе ABCDA1B1C1D1 из вершины D1 проведены диагонали граней D1А, D1С и D1В1, а их концы соединены отрезками.
Доказать, что многогранник D1АВ1С-правильный тетраэдр.
Найти отношение площадей поверхностей куба и тетраэдра.
I) Докажем, что многогранник D1АВ1С-правильный тетраэдр.
Вы уже знаете, что все грани куба- это равные квадраты.
Диагонали этих квадратов так же будут равными.
А так как эти равные диагонали являются рёбрами многогранника D1АВ1С, следовательно данный многогранник D1АВ1С-правильный тетраэдр.
Что и требовалось доказать.
II) Найдем отношение площадей куба и тетраэдра.
1)Пусть а –ребро куба.
Из равнобедренного прямоугольного треугольника АВС найдем АС по теореме Пифагора:
АС= = =а -ребро тетраэдра.
2)Найдем площадь куба, которая составлена из площади 6 равных квадратов.
Sкуба=6а2
3) Найдём площадь тетраэдра, которая состоит из четырёх равных треугольников АВ1С.
В свою очередь, треугольник АВ1С –равносторонний, сторона которого равна диагонали квадрата и равна а , а каждый его угол равен 60 градусов. Тогда площадь треугольника равна:
SAB1C = •АВ1•В1С•sin 600= •а •а • = •a2
Значит, площадь боковой поверхности тетраэдра D1 АВ1С равна:
Sтетр= 4∙SAB1C= 4• •a2=2а2
4) Найдем отношение площадей куба и тетраэдра:
Таким образом, отношение площадей куба и тетраэдра равно √3.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7398 |
| Номер материала | 947 |