
Урок «Некоторые следствия из аксиом»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы познакомимся со следствиями из аксиом стереометрии и их доказательствами, применим эти свойства при решении задач.
Их мы сформулируем в виде теорем.
Первое следствие из аксиом.
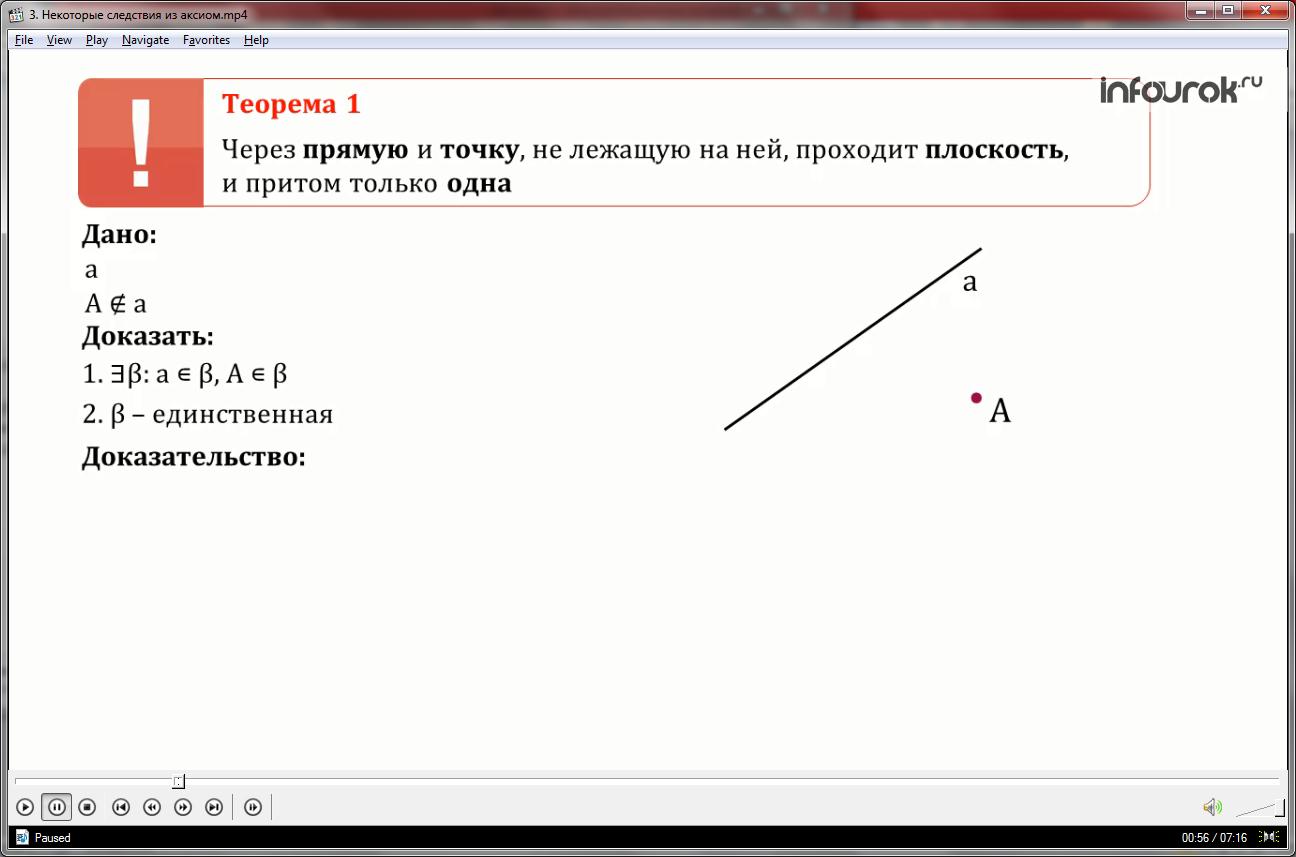
Теорема 1. Через прямую и точку, не лежащую на ней, проходит плоскость, и притом только одна.
Дано:
прямая a
точка A не принадлежащая на прямой a
Доказать: Существует единственная плоскость , проходящая через прямую a и точку A
Доказательство
1. Докажем существование плоскости.
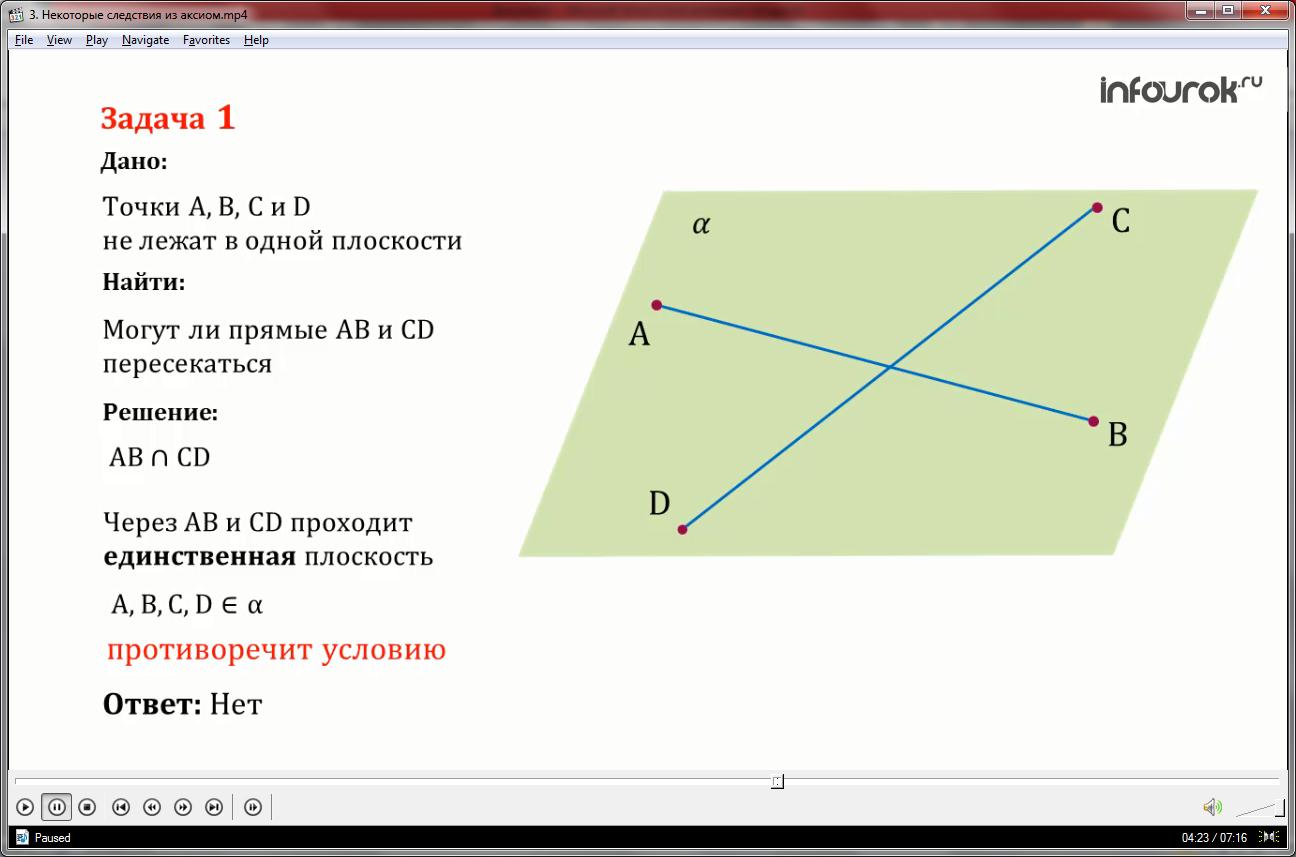
Отметим на прямой a любые две точки B и C.
Так как три точки A, B, C не лежат на одной прямой, то существует плоскость , проходящая через эти точки. Это следует из аксиомы А1.
Так как две точки B и C прямой a принадлежат плоскости , то плоскость проходит через прямую a (по аксиоме А2).
Итак, плоскость проходит через прямую a и точку A.
– искомая плоскость.
2. Докажем единственность плоскости.
Любая плоскость, проходящая через прямую a и точку A проходит через три точки: B, C и A.
Мы знаем, что через три точки проходит единственная плоскость. Это следует из аксиомы А1.
Поэтому плоскость совпадет с плоскостью α.
Теорема доказана.
Второе следствие из аксиом.
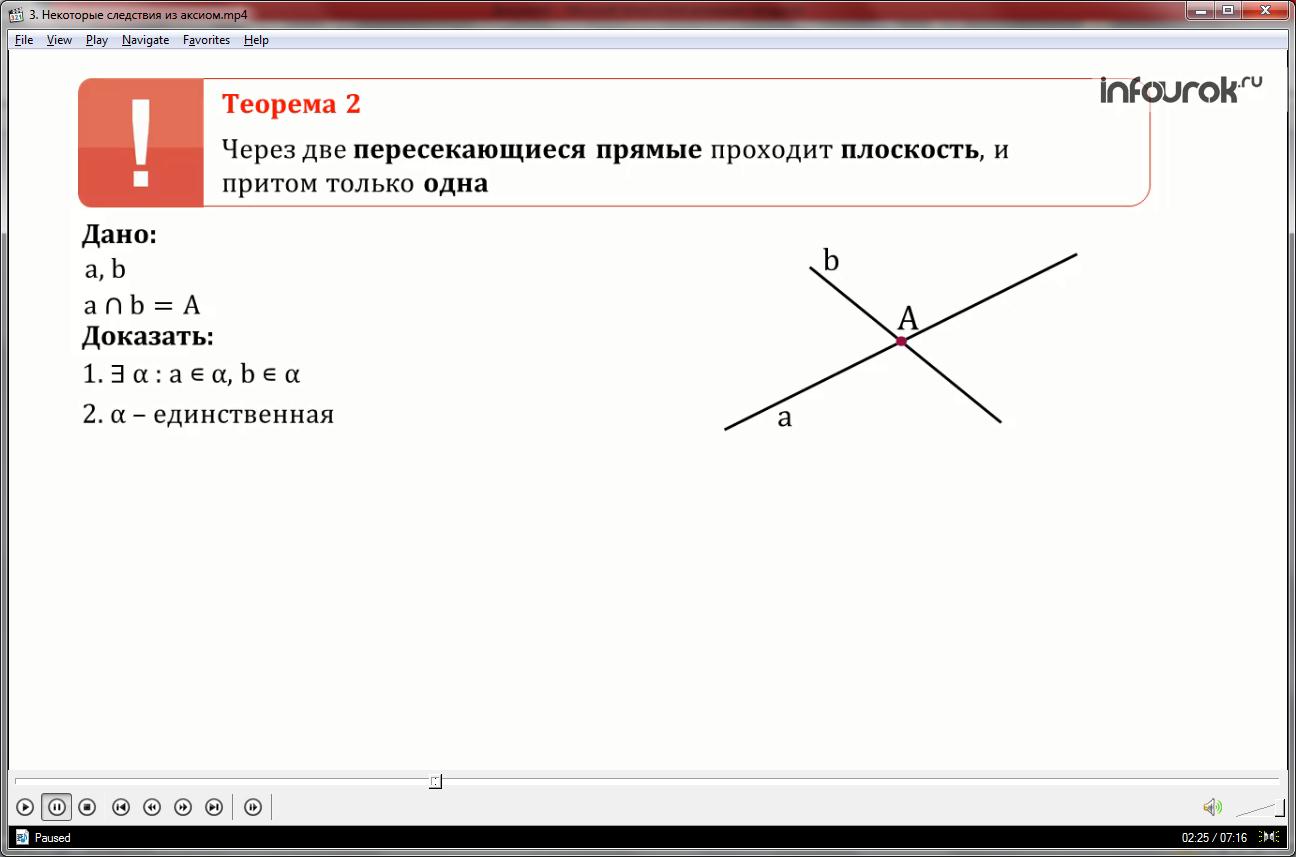
Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Дано:
Прямые a и b, пересекающиеся в точке A.
Докажем, что через эти прямые проходит плоскость, и притом только одна
Доказательство.
1.Докажем, что такая плоскость существует.
На прямой b отметим произвольную точку B, отличную от A.
Через точку B и прямую a мы можем провести плоскость . По первой теореме.
Так как две точки A и B прямой b принадлежат плоскости , то плоскость проходит через прямую b.
Получается, плоскость проходит через обе прямые.
– искомая плоскость.
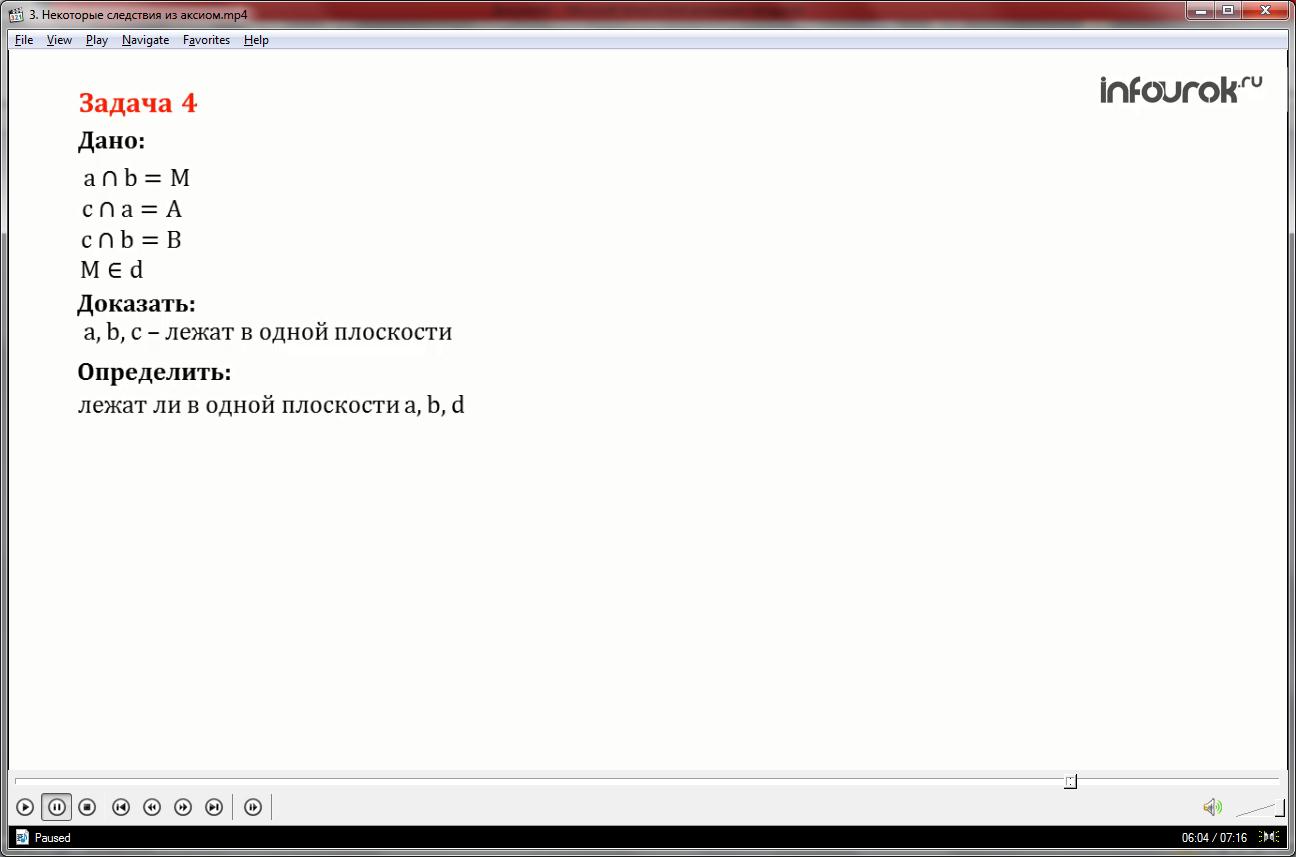
2.Теперь докажем, что такая плоскость единственная.
Допустим противное: существует другая плоскость, например плоскость β, которая проходит через прямые a и b.
Тогда плоскость β должна проходить и через точку B.
Через прямую a и точку B проходит единственная плоскость (по теорема 1). Поэтому плоскость β совпадает с плоскостью α.
Противоречие. Мы предполагали, что плоскости разные.
Значит, исходное предположение неверное. Плоскость – единственная.
Теорема доказана.
Перейдем к решению задач.
Мы можем опираться, пока, на три аксиомы, две теоремы, которые доказали и все факты планиметрии.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 13168 |
| Номер материала | 917 |