
Урок «Параллелепипед»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Рассмотрим эти предметы:
Строительный кирпич, игральный кубик, микроволновая печь. Эти предметы объединяет форма.
Поверхность, состоящая из двух равных параллелограммов АВСD и А1В1С1D1
и четырех параллелограммов АА1В1В и ВВ1С1С, СС1D1D, АА1D1D называется параллелепипедом.
Параллелограммы, из которых составлен параллелепипед, называются гранями. Грань А1В1С1D1. Грань ВВ1С1С. Грань АВСD.
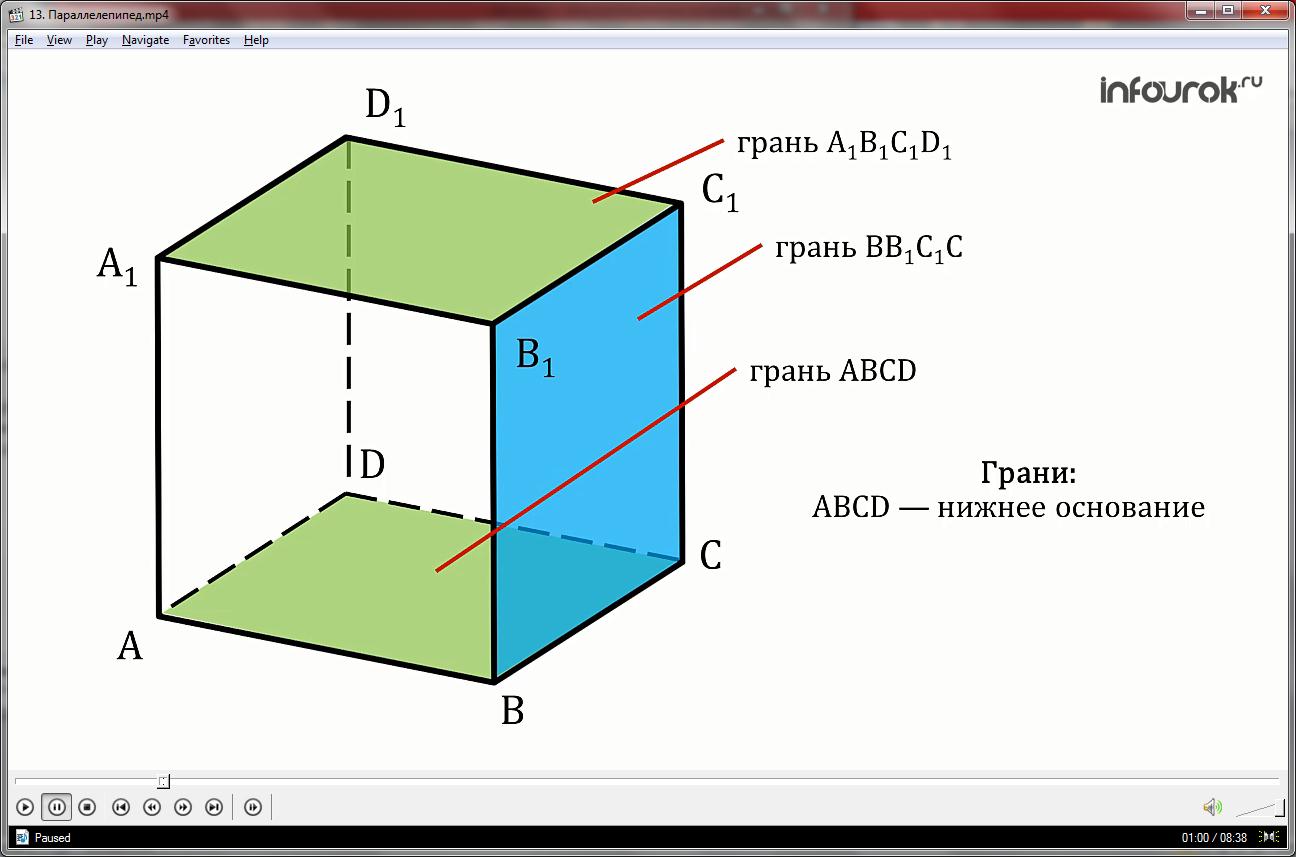
При этом грани АВСD и А1В1С1D1 чаще называют основаниями, а остальные грани боковыми.
Стороны параллелограммов называются ребрами параллелепипеда. Ребро А1В1. Ребро СС1. Ребро АD.
Ребро СС1, не принадлежит основаниям, оно называются боковое ребро.
Вершины параллелограммов называют вершинами параллелепипеда.
Вершина D1. Вершина В. Вершина С.
Вершины D1 и В
не принадлежат одной грани и называются противоположными.
Параллелепипед можно изображать разными способами
Параллелепипед в основании, которого лежит ромб, При этом изображениями граней являются параллелограммы.
Параллелепипед в основании, которого лежит квадрат. Невидимые рёбра АА1, АВ, АD изображаются штриховыми линиями.
Параллелепипед в основании, которого лежит квадрат
Параллелепипед в основании, которого лежит прямоугольник или параллелограмм
Параллелепипед, у которого все грани квадраты. Чаще его называют кубом.
Все рассмотренные параллелепипеды обладают свойствами. Сформулируем и докажем их.
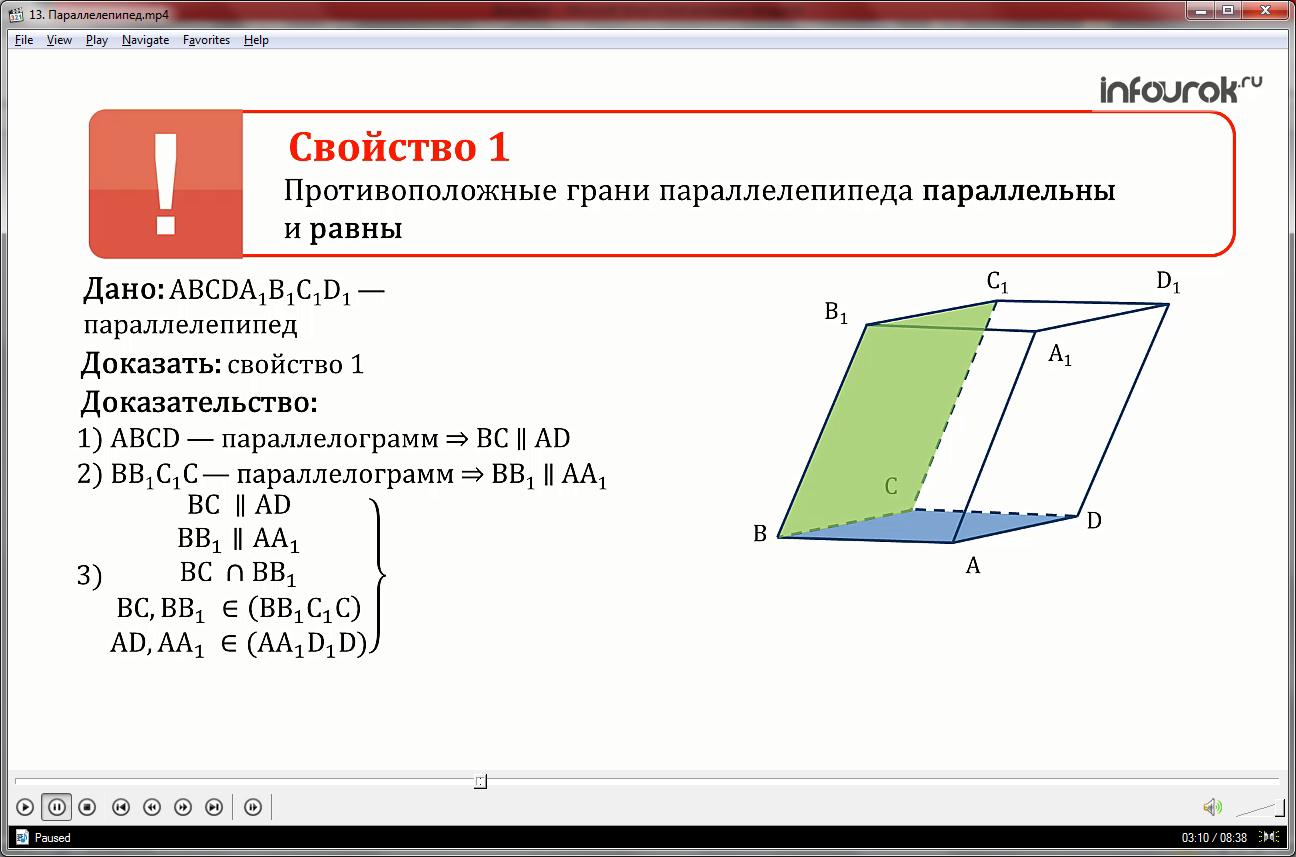
Свойство 1. Противоположные грани параллелепипеда параллельны и равны.
Рассмотрим параллелепипед АВСDА1В1С1D1 и докажем, например, параллельность и равенство граней ВВ1С1С и АА1D1D.
По определению параллелепипеда грань АВСD параллелограмм, значит по свойству параллелограмма ребро ВС параллельно ребру АD.

Грань АВВ1А1 тоже параллелограмм, значит ребра ВВ1 и АА1 параллельны.
Это означает что две пересекающиеся прямые ВС и BB1 одной плоскости соответственно параллельны двум прямым АD и АА1 соответственно другой плоскости, значит плоскости АВВ1А1 и ВСС1D1 параллельны.
Все грани параллелепипеда параллелограммы а значит ВС=АD, ВВ1 =АА1.
При этом стороны углов В1ВС и А1АD соответственно сонаправлены, значит они равны.
Таким образом, две смежные стороны и угол между ними параллелограмма АВВ1А1 соответственно равны двум смежным сторонам и углу между ними параллелограмма ВСС1D1, значит эти параллелограммы равны.
Параллелепипед обладает ещё свойством о диагоналях . Диагональю параллелепипеда называется отрезок соединяющий не соседние вершины. На чертеж пунктирной линией показаны диагонали В1D, BD1, А1С.
Итак, свойство 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Для доказательства свойства рассмотрим четырехугольник ВВ1D1D. Его диагонали В1D, BD1 являются диагоналями параллелепипеда АВСDА1В1С1D1.
В первом свойстве мы уже выяснили, что ребро ВВ1 параллельно и равно ребру АА1, но ребро АА1 параллельно и равно ребру DD1. Следовательно рёбра ВВ1 и DD1 параллельны и равны, что доказывает четырехугольник ВВ1D1D– параллелограмм. А в параллелограмме по свойству диагонали В1D, BD1 пересекаются в некоторой точке О и этой точкой делятся пополам.
Четырехугольник ВС1D1А также является параллелограммом и его диагонали С1А, пересекаются в одной точке и делятся этой точкой пополам. Диагонали параллелограмма С1А, ВD1 являются диагоналями параллелепипеда, а значит сформулированное свойство доказано.
Для закрепления теоретических знаний о параллелепипеде рассмотрим задачу на доказательство.
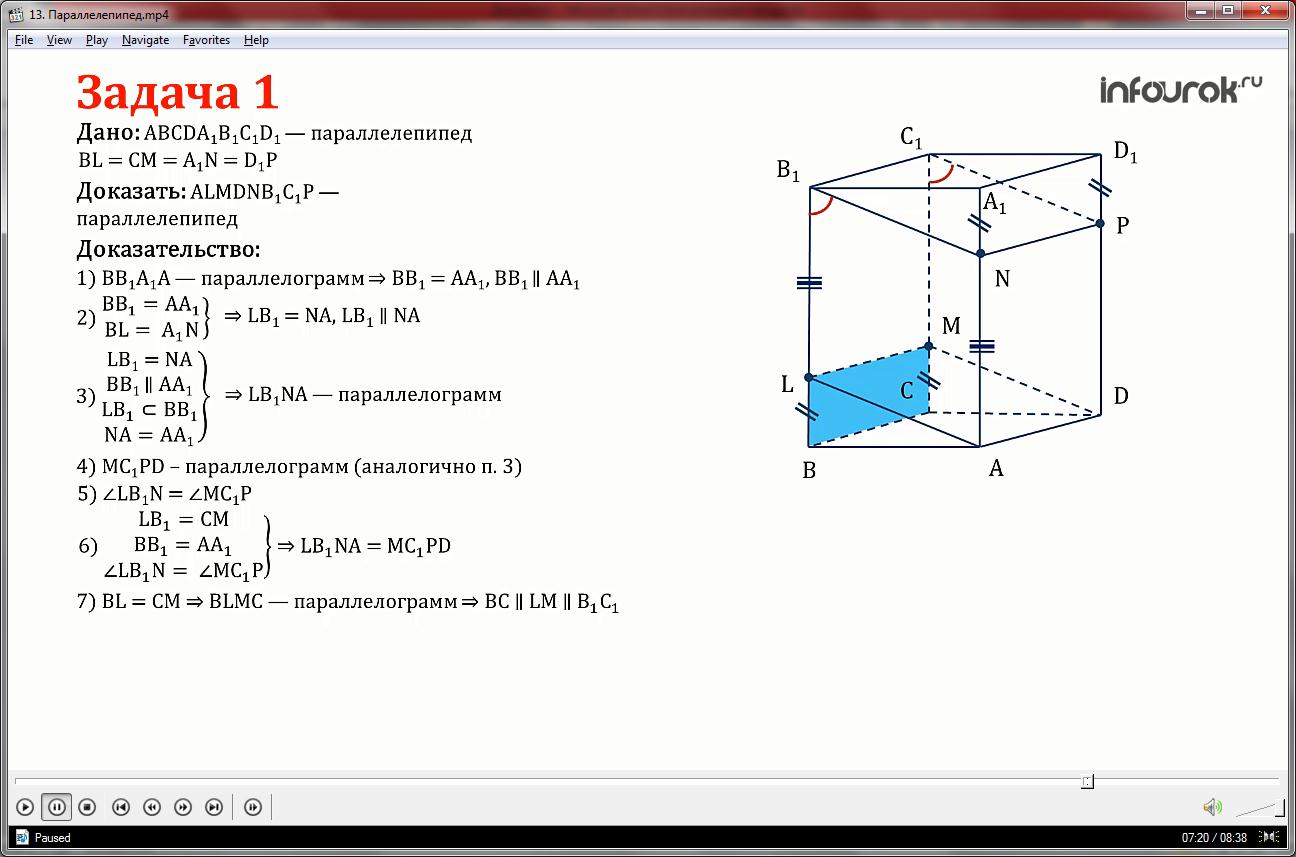
На рёбрах параллелепипеда отмечены точки L,M,N,P так, что BL=CM=A1N=D1P. Доказать, что ALMDNB1C1P параллелепипед.
Грань ВВ1А1А параллелограмм, значит ребро ВВ1 равно и параллельно ребру АА1, но по условию отрезки BL и A1N, значит равны и параллельны отрезки LB1 и NA.
3)Следовательно, четырехугольник LB1NA по признаку параллелограмм.
4) Так как СС1D1D–параллелограмм, значит ребро СС1 равно и параллельно ребру D1D, а СМ равно D1P по условию, значит равны и параллельны отрезки МС1и DP
Следовательно, что четырехугольник MC1PD тоже параллелограмм.
5) Углы LB1N и MC1P равны как углы с соответственно параллельными и одинаково направленными сторонами.
6) Мы получили, что у параллелограммов и MC1PD соответствующие стороны равны и углы между ними равны, значит параллелограммы равны.
7) Отрезки равны по условию, значит BLMC- параллелограмм и сторона BC параллельна стороне LM параллельна стороне В1С1.
8) Аналогично из параллелограмма NA1D1P следует, что сторона A1D1 параллельна стороне NP и параллельна стороне AD.
9)Противоположные грани ABB1A1 и DCC1D1 параллелепипеда по свойству параллельны, а отрезки параллельных прямых заключенных между параллельными плоскостями равны, значит отрезки В1С1, LM, AD,NP равны.
Получено, что в четырехугольниках ANPD, NB1C1P, LB1C1M, ALMD две стороны параллельны и равны , значит они параллелограммы. Тогда наша поверхность ALMDNB1C1P состоит из шести параллелограммов , два из которых равны, а по определению это параллелепипед.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 19884 |
| Номер материала | 927 |