
Урок «Параллельные плоскости»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем понятие параллельных плоскостей
Согласно аксиоме A3, если две плоскости имеют общую точку, то они пересекаются по прямой.
Отсюда следует, что плоскости либо пересекаются по прямой, либо не пересекаются, т. е. не имеют ни одной общей точку.
Определение. Две плоскости называются параллельными, если они не пересекаются.
Если плоскости параллельны, пишут: .
Теорема (признак параллельности плоскостей).
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Доказательство.
Рассмотрим две плоскости: .
В плоскости лежат пересекающиеся прямые a1 и b1, а в плоскости параллельные им пересекающиеся прямые a2и b2.
Докажем, что .
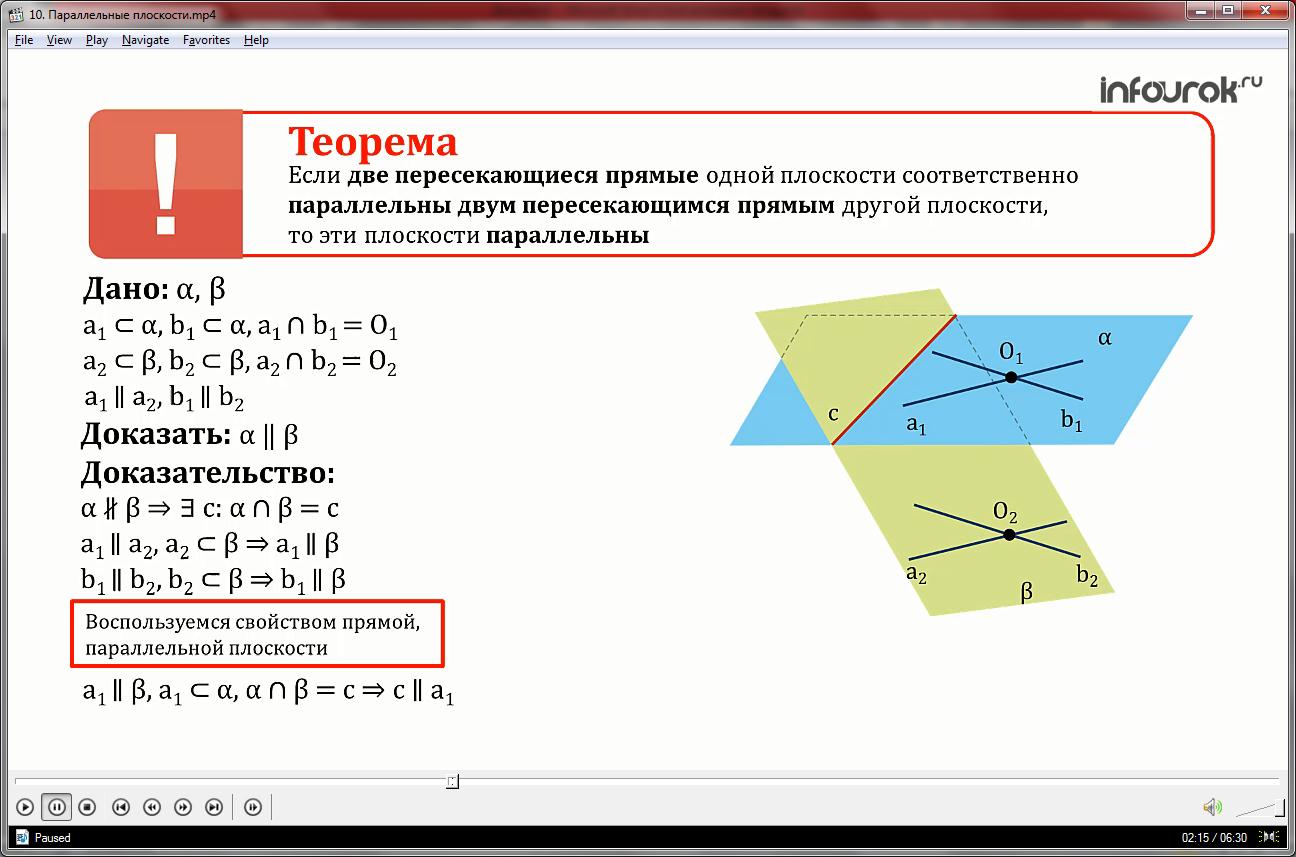
Доказательство. Рассуждаем методом от противного.
Предположим, что плоскости не параллельны. Тогда существует прямая c, по некоторой они пересекаются.
Так как прямая a1 параллельна прямой a2 , лежащей в плоскости , то прямая a1 параллельна плоскости .
Аналогично, прямая b1 параллельна плоскоcти .
Теперь можно воспользоваться свойством прямой, параллельной плоскости.
Так как плоскость проходит через прямую a1, параллельную другой плоскости , и пересекает эту плоскость, то линия пересечения плоскостей c будет параллельна прямой a1, т.е.
Но плоскость проходит и через прямую b1, параллельную плоскости , поэтому .
Таким образом, через точку O1 проходят две прямые a1 и b1 , параллельные прямой c.
Но это невозможно, через O1 может проходить только одна прямая, параллельная с.
Предположив, что мы пришли к противоречию. Следовательно, .
Теорема доказана.
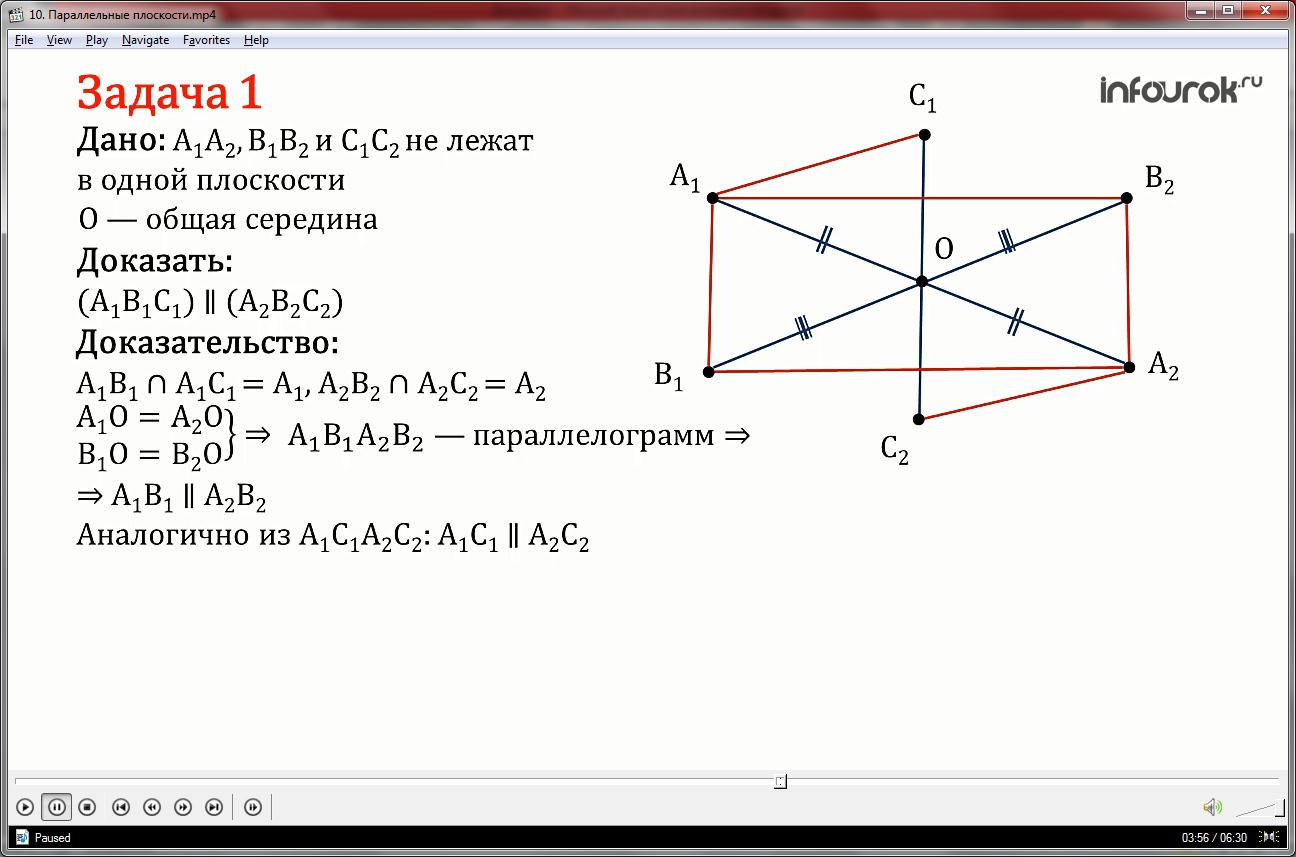
Задача 1. Три отрезка A1A2, B1B2 и C1C2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости A1B1C1 и A2B2C2 параллельны.
Дано:
Отрезки A1A2, B1B2 и C1C2 не лежат в одной плоскости
O – общая середина отрезков
Доказать: Плоскость A1B1C1 плоскости A2B2C2
Решение.
В плоскости A1B1C1возьмем пересекающиеся отрезки A1B1 и A1C1 , а в плоскости A2B2C2 – отрезки A2B2 и A2C2. Докажем, что они соответственно параллельны.
Рассмотрим четырехугольник A1B1A2B2.
Так как его диагонали в точке пересечения делятся пополам, то это параллелограмм.
Поэтому A1B1 A2B2
Аналогично из четырехугольника A1C1A2C2 получим, что A1C1 A2C2.
По признаку параллельности плоскостей,
A1B1C1 A2BC2
Ч.т.д.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 12382 |
| Номер материала | 924 |