
Урок «Параллельные прямые в пространстве»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введём определение параллельных прямых в пространстве:
- Две прямые в пространстве называются параллельными, если
они лежат в одной плоскости и
и не пересекаются
Обозначаются параллельные прямые также как и в планиметрии
Рассмотрим куб.
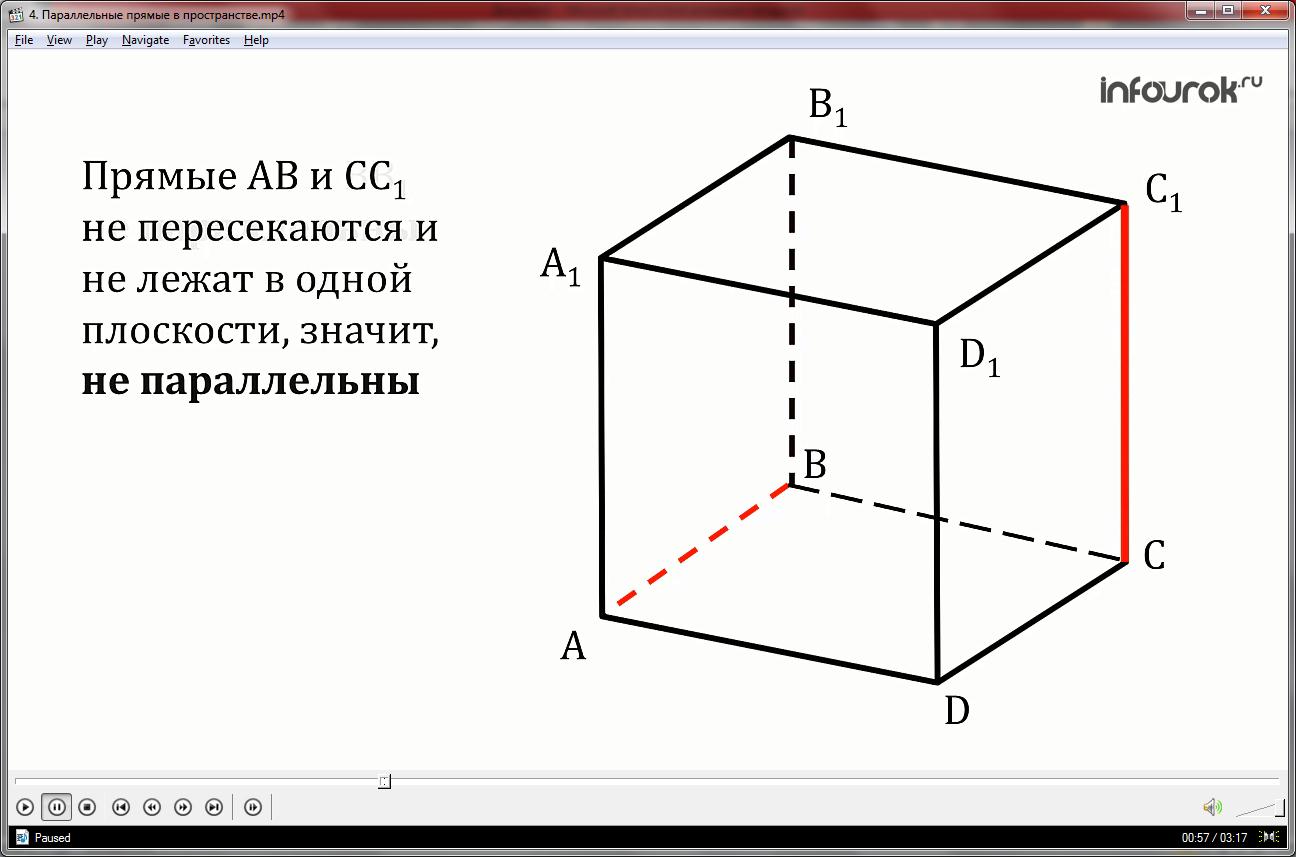
Прямые АА1 и СС1 параллельны. Согласно определению, они лежат в одной плоскости АА1С и не пересекаются.
Прямые АВ и ВВ1 не параллельны, так как хоть они лежат в одной плоскости, но пересекаются в точке В.
Прямые АВ и СС1 не пересекаются и не лежат в одной плоскости, значит, не параллельны.
Вспомним из курса планиметрии аксиому параллельных прямых: «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной».
Аксиома поможет доказать теорему параллельных прямых.
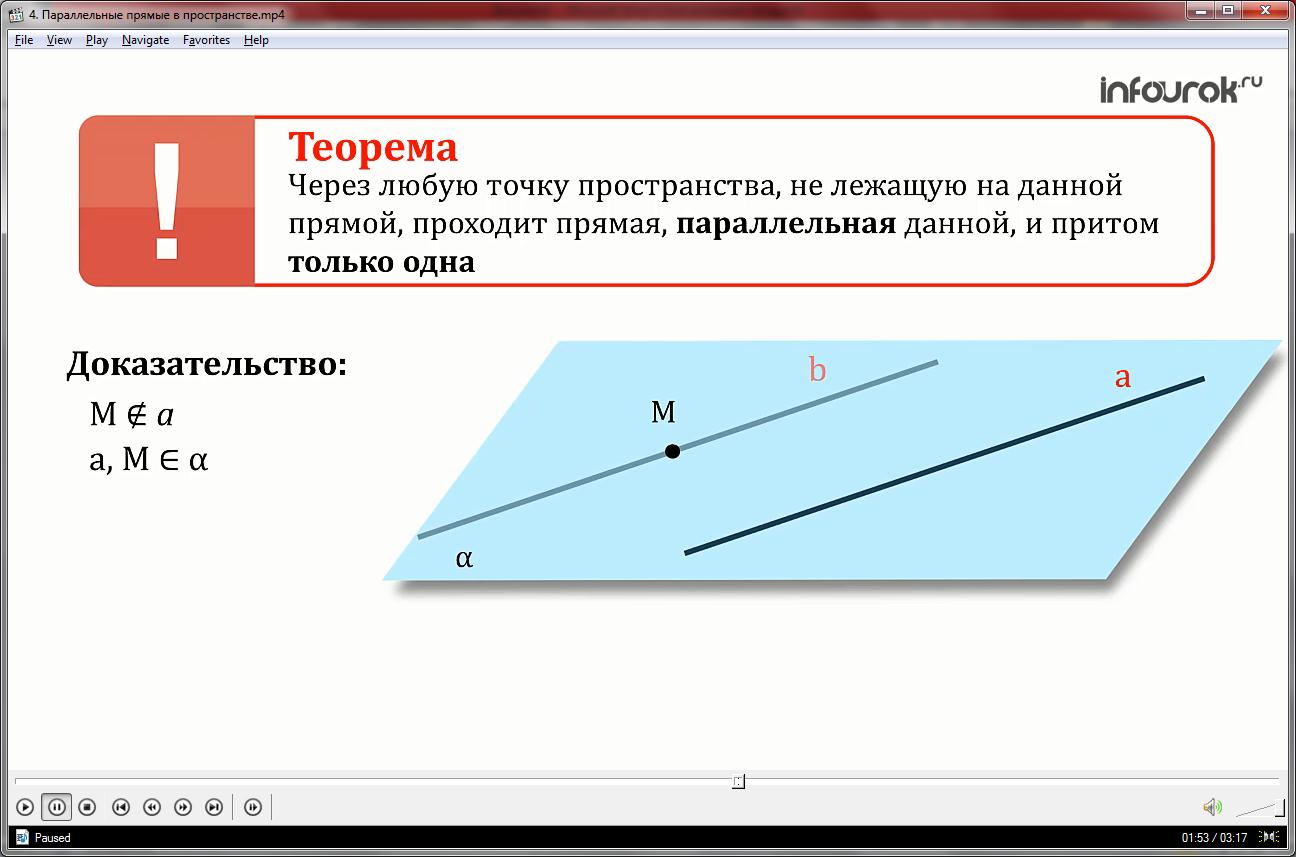
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Докажем эту теорему.
Рассмотрим прямую а и точку М, которая не лежит на этой прямой. Согласно следствию из аксиом стереометрии, через прямую а и точку М проходит плоскость, и притом только одна. Через точку М проведем прямую b, параллельную прямой а. Прямая b из условия параллельности лежит в одной плоскости с прямой а. Единственность этой прямой следует из аксиомы параллельных прямых из курса планиметрии. Прямая, параллельная данной существует и она единственная.
Теорема доказана.
Для решения задач потребуется определение параллельных отрезков.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Задача
Параллельные прямые a и b лежат в плоскости . Докажите, что прямая c, пересекающая прямые a и b, также лежит в плоскости .
Решение.
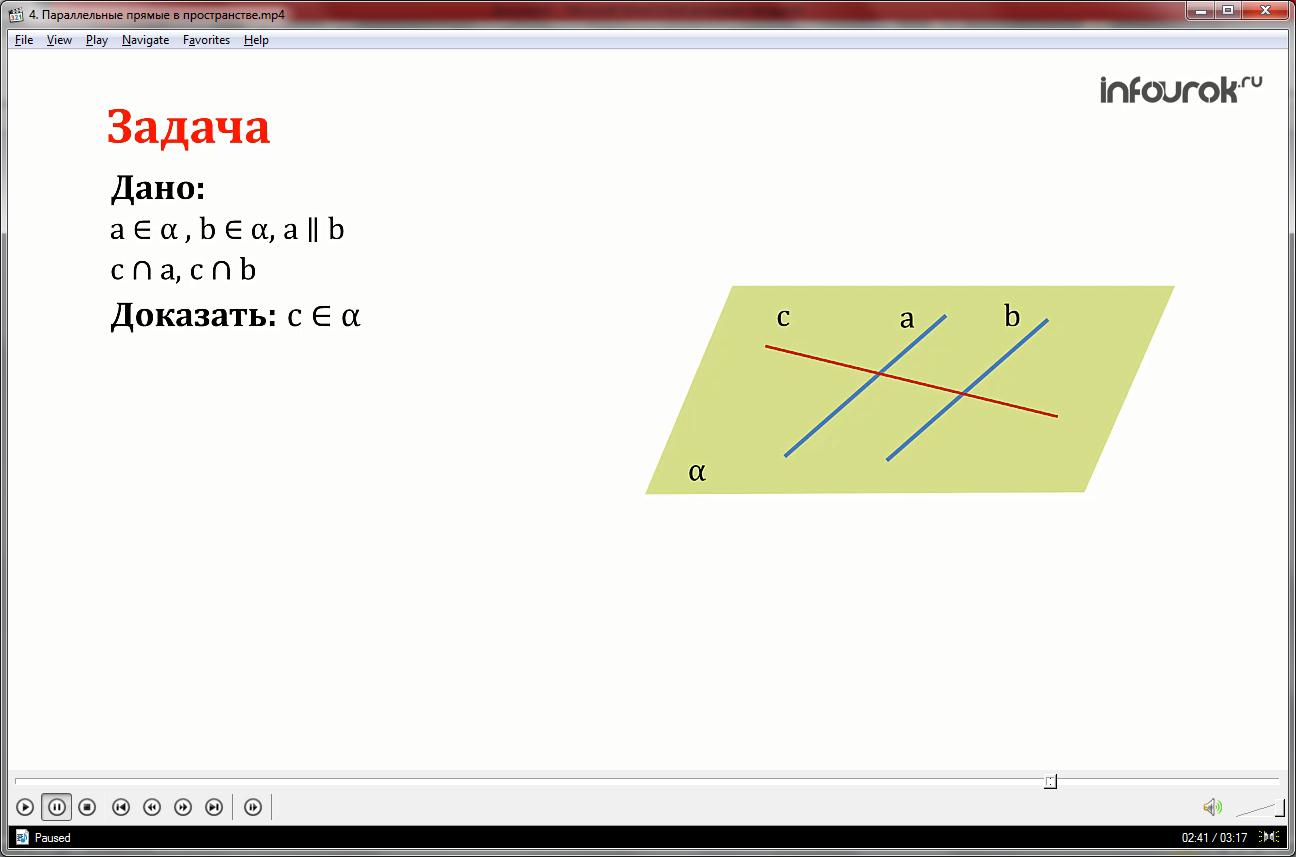
Так как прямая а лежит в плоскости альфа и прямая с пересекает прямую а, то точка их пересечения лежит в плоскости альфа.
Аналогично точка пересечения b и с лежи в плоскости альфа.
И по аксиоме А2 (если две точки прямой лежат в плоскости, то все точки прямой лежат в это плоскости) следует что прямая с лежит в плоскости альфа.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 12422 |
| Номер материала | 918 |