
Урок «Параллельность прямой и плоскости»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
В этом уроке мы рассмотрим возможные случаи взаимного расположения прямой и плоскости в пространстве, введем понятие параллельности прямой и плоскости, докажем признак параллельности прямой и плоскости.
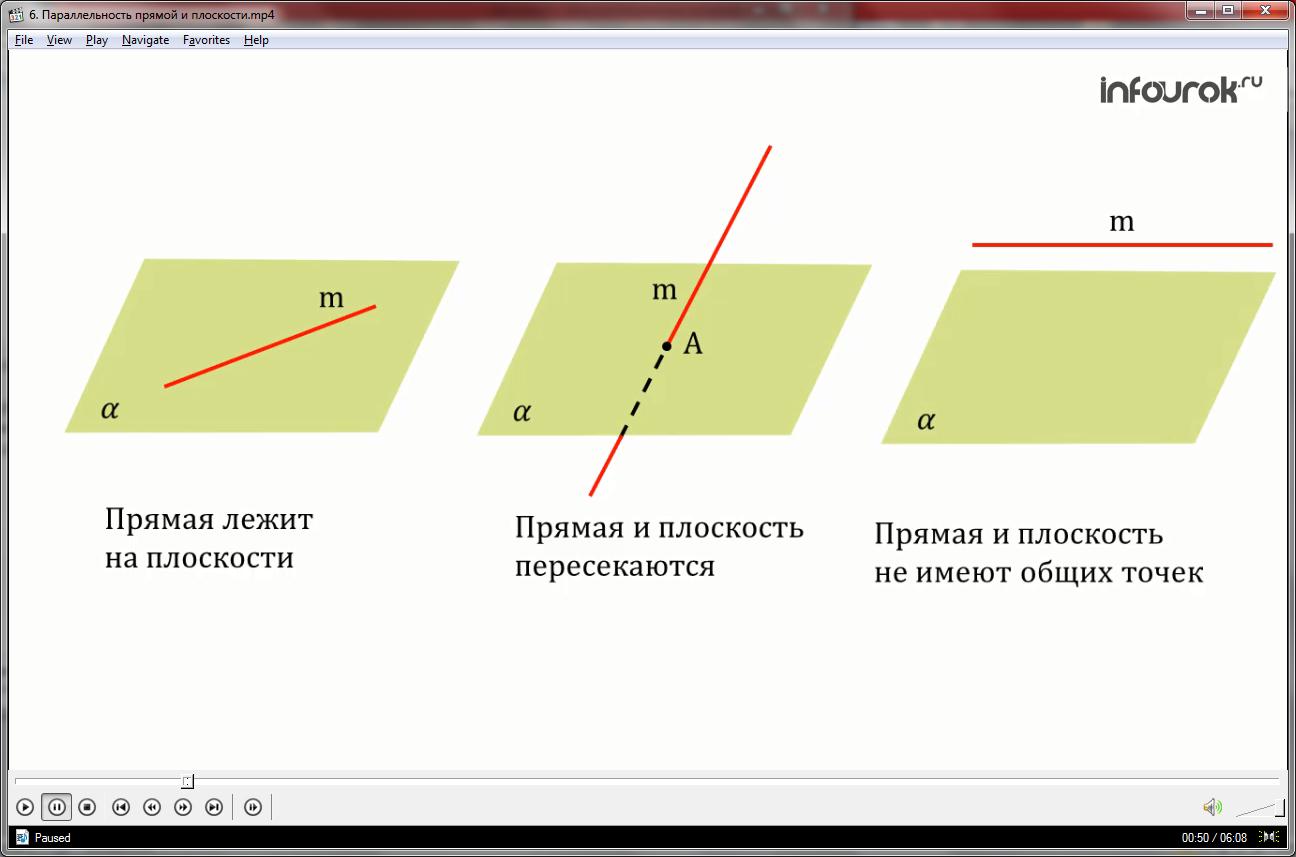
Возможны три случая взаимного расположения прямой и плоскости в пространстве:
1.Прямая лежит на плоскости;
2.Прямая пересекает плоскость, т. е. прямая и плоскость имеют одну общую точку;
3.Прямая и плоскость не имеют общих точек.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек
Параллельность прямой A и плоскости обозначается так:
Теорема (признак параллельности прямой и плоскости) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Дано:
Плоскость
Прямая c не лежит в плоскости
Прямая d лежит в этой плоскости
β параллельна d
Доказать: Прямая a параллельна плоскости
Доказательство.
Доказательство будем вести от противного.
Предположим: прямая c не параллельна плоскости . Тогда она пересекает плоскость в некоторой точке F.
По лемме о пересечении плоскости параллельными прямыми, прямая d также пересекает эту плоскость.
Пришли к противоречию, по условию d лежит в плоскости . Предположение не верно, прямая c параллельна плоскости .
Что и требовалось доказать.
Докажем еще два утверждения, которые часто используются при решении задач.
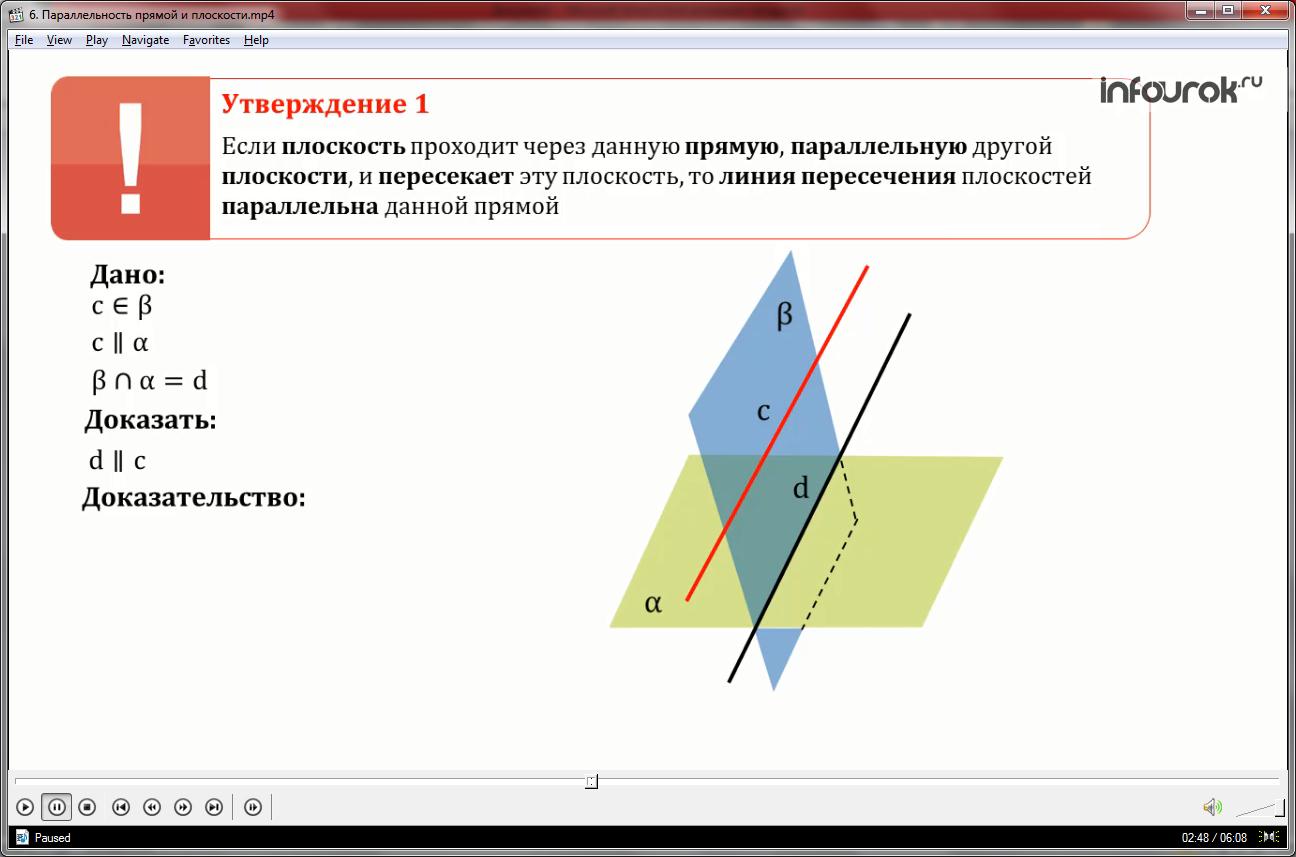
1.Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то лини пересечения плоскостей параллельна данной прямой.
Доказательство.
По определению, прямые называются параллельными, если:
1) прямые лежат в одной плоскости;
2) прямые не пересекаются.
Так как по условию плоскость проходит через прямую c, а прямая d является общей для плоскостей то c и d лежат в одной плоскости.
Так как прямая c параллельна плоскости , в которой лежит прямая d, то c и d не пересекаются.
Оба условия параллельности выполняются.
Можно сделать заключение:
Что и требовалось доказать
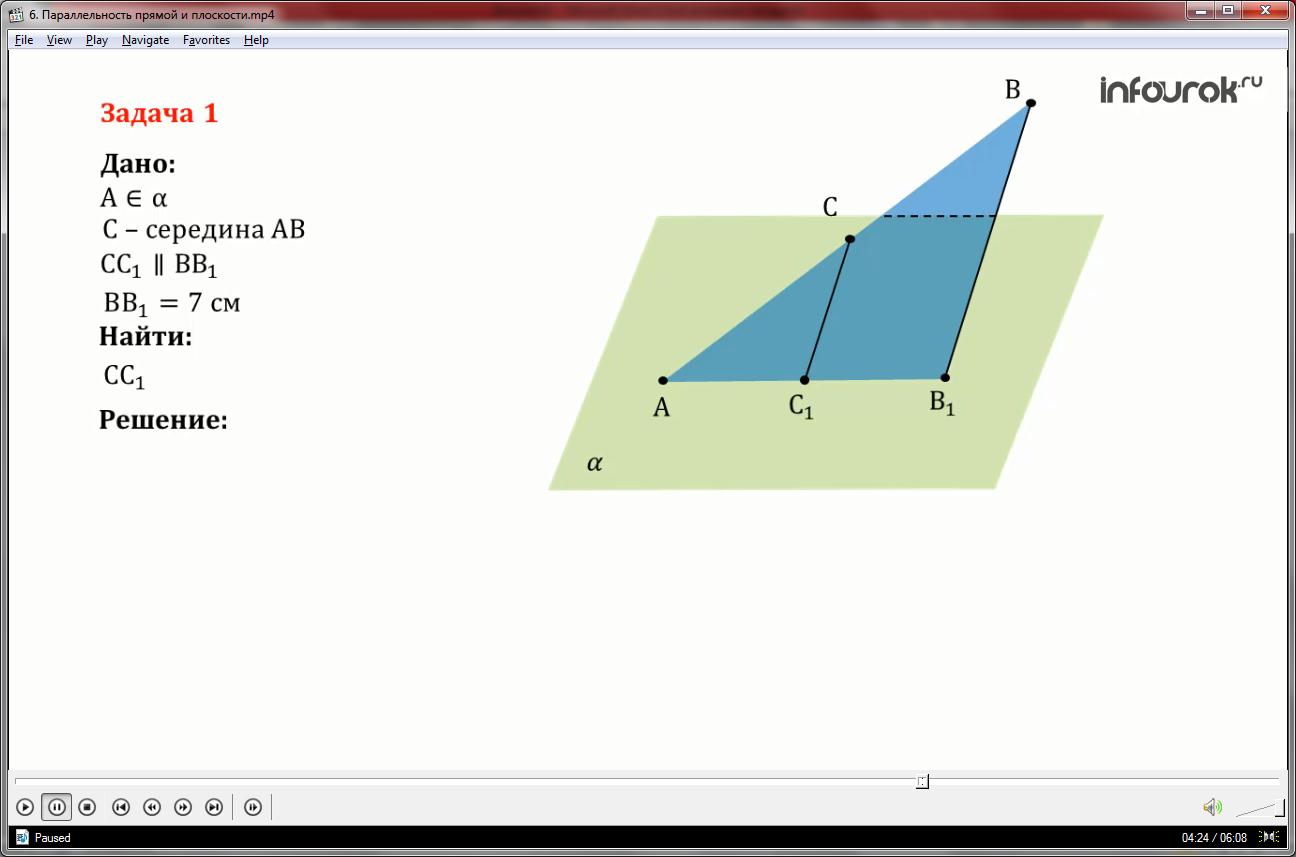
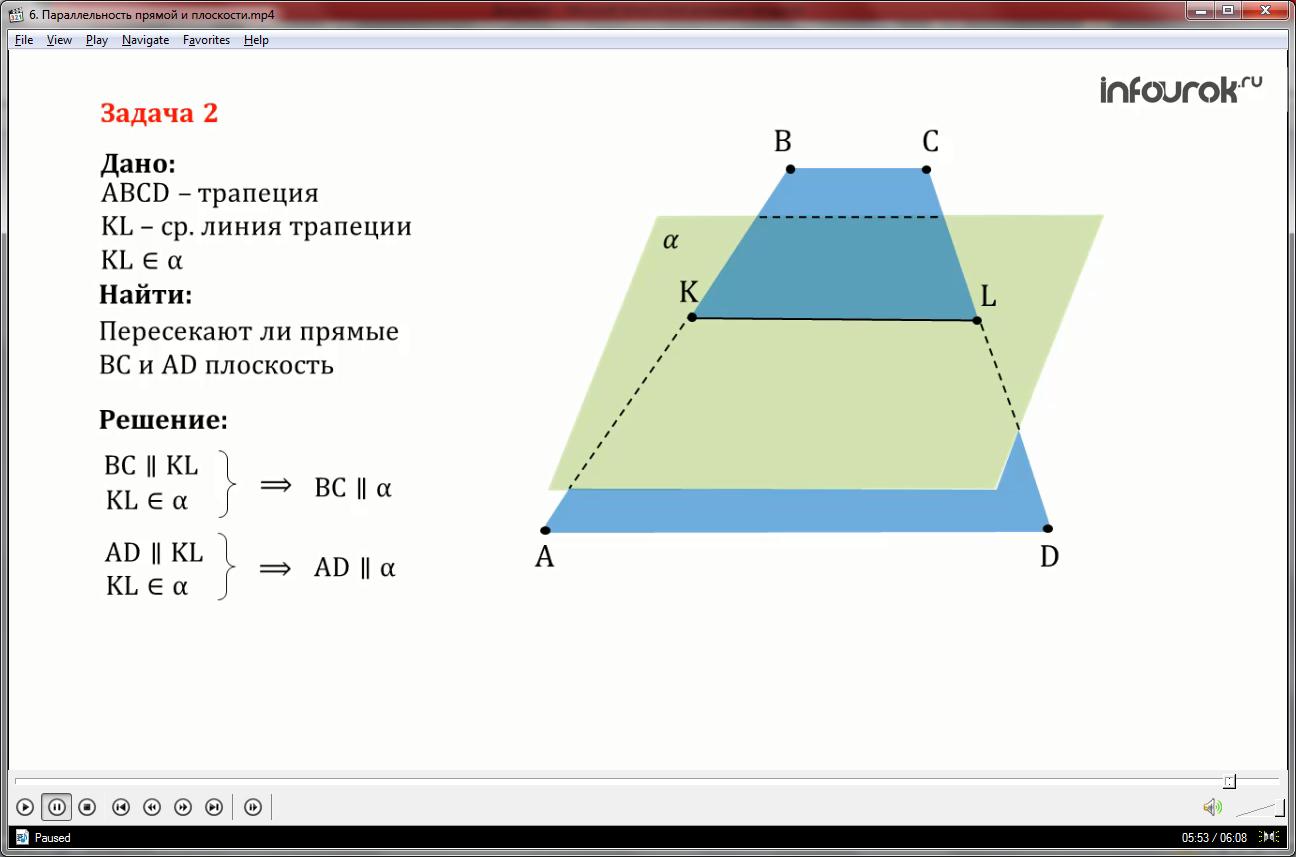
2.Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая также параллельна данной плоскости, либо лежит в этой плоскости.
Дано:
Доказать:
Доказательство.
Так как , то прямая a не пересекается с плоскостью .
Если a не пересекает плоскость, то и параллельная ей прямая b ее не пересекает( по лемме о пересечении плоскости параллельными прямыми).
Поэтому прямая b либо параллельна плоскости, либо лежит в ней.
Что и требовалось доказать.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 16717 |
| Номер материала | 920 |