
Урок «Параллельность трех прямых»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Параллельность трех прямых
Докажем лемму о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает данную плоскость.

Рассмотрим параллельные прямые а и b, одна из которых (прямая а) пересекает плоскость . Докажем, что и прямая b пересекает эту плоскость, то есть имеют одну общую точку
1)Пусть прямая а пересекает плоскость в точке М. Прямые а и b лежат в одной плоскости, назовем её . Плоскости и имеют общую точку М, значит, они пересекаются по прямой с.
2)Прямая с лежит в плоскости и пересекает прямую а, значит она пересекает и параллельную ей прямую b в точке Р.
3) Прямая с лежит и в плоскости альфа. Поэтому точка Р принадлежит также плоскости альфа. Если предположить, что существует ещё одна точка, принадлежащая и прямой b и плоскости альфа, то это означает, что прямая b лежит в этой плоскости и совпадает с прямой с и пересекает прямую а. А это противоречит условию. Точка Р – точка пересечения прямой b и плоскости альфа.
Что и требовалось доказать.

Эта лемма поможет доказать теорему о параллельности трёх прямых в пространстве.
Если две прямые параллельны третьей прямой, то они параллельны.
Докажем эту теорему.
Пусть прямая а параллельна прямой с и прямая b параллельна прямой с. Докажем, что а параллельна b.
Доказательство. Для этого нужно доказать, что они лежат в одной плоскости и не пересекаются.
1) Отметим точку К на прямой b. Точка К и прямая а определяют плоскость, обозначим её .
Докажем, что прямая b лежит в этой плоскости.
2) Допустим прямая b не лежит, а пересекает эту плоскость. По лемме о параллельных прямых, прямая с, параллельная b, также пересекает эту плоскость. Но тогда и прямая а, параллельная с тоже пересекает плоскость альфа. Противоречие с условием задания плоскости. Значит прямая b лежит в плоскости. Прямые а и b не пересекаются, так как иначе через точку их пересечения проходило бы две прямые, параллельные прямой с, что противоречит теореме параллельных прямых. Теорема доказана
Решим задачу.
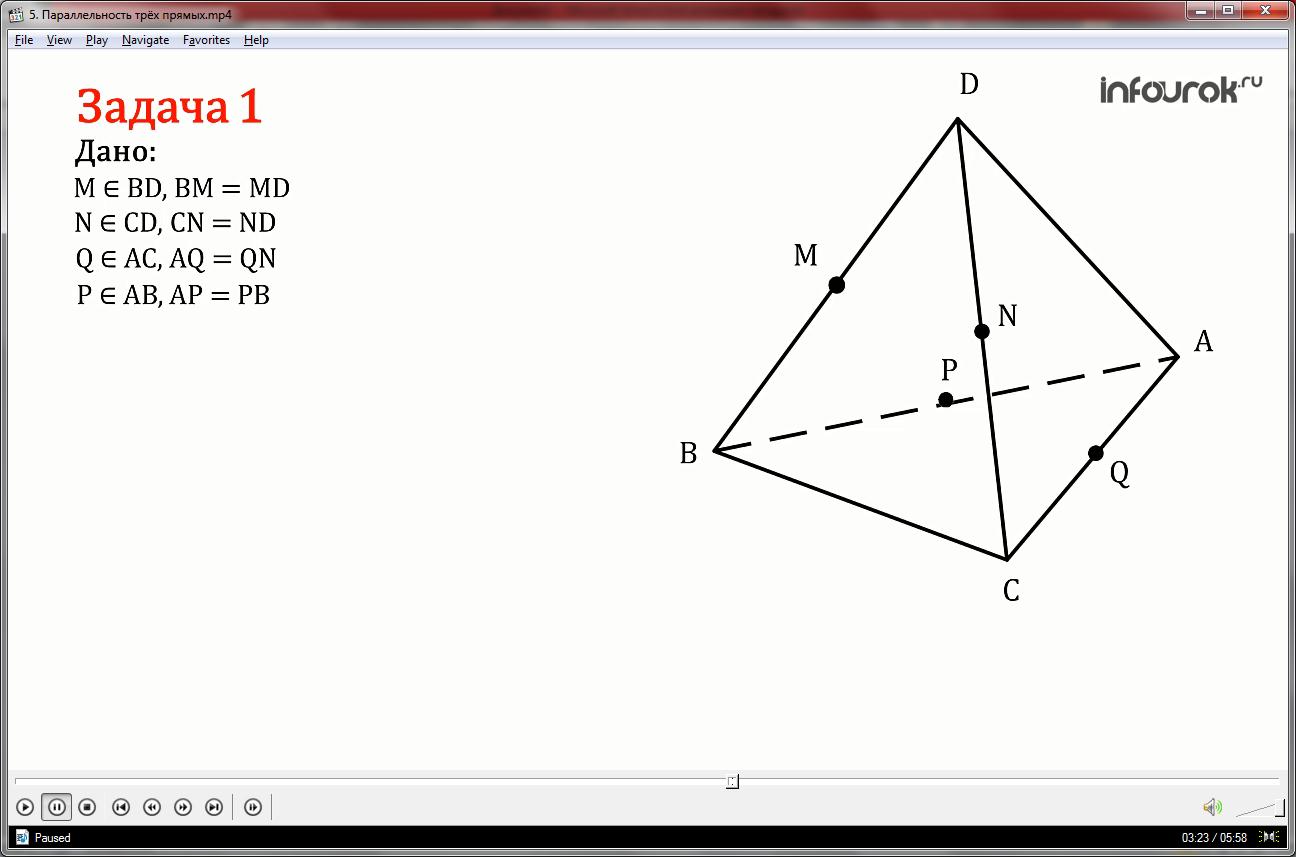
Задача 1
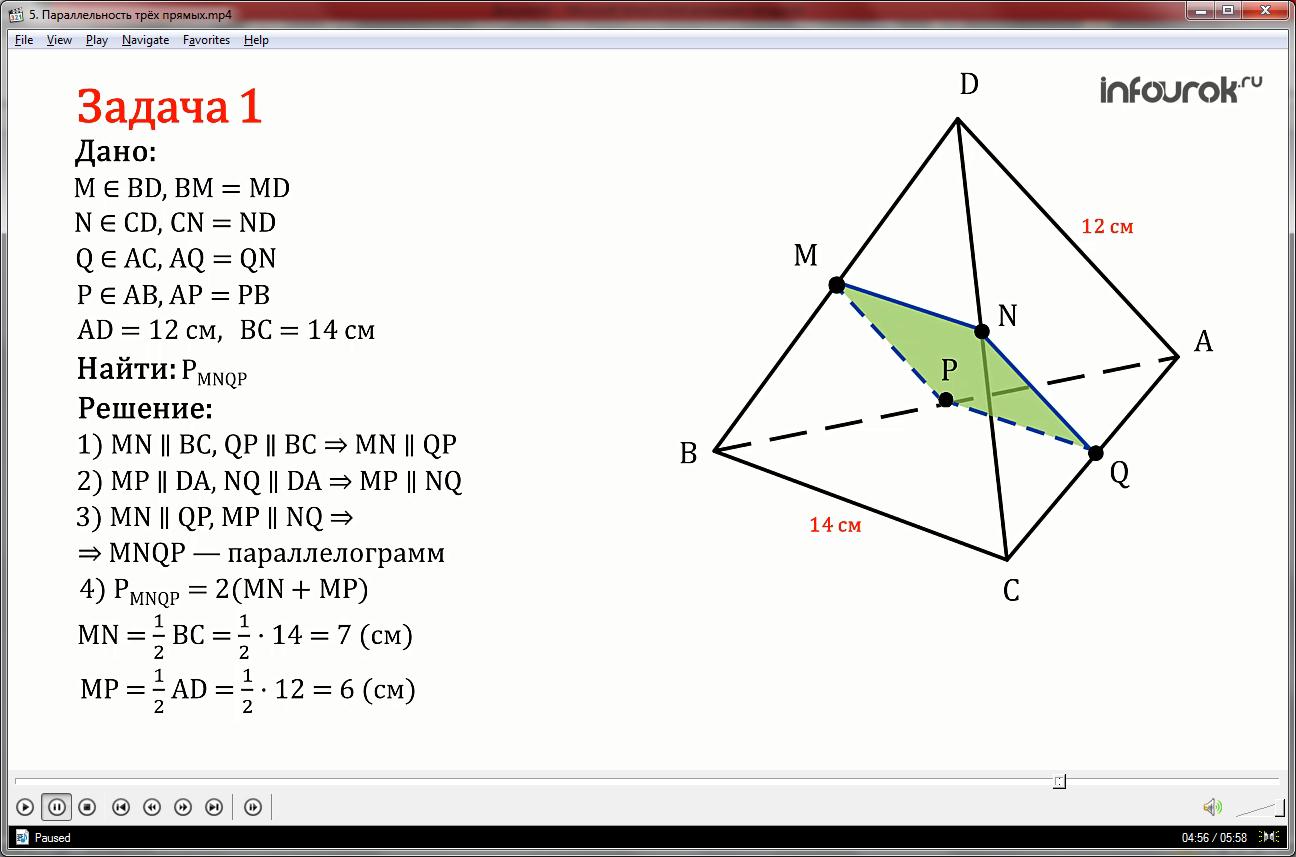
На рисунке точки M, N, Q и Р – середины ребер DP, DC, AC, AB. Найдите периметр четырехугольника MNQP, если AD= 12 см, BC= 14 см.
Решение:
1) Рассмотрим треугольник ВСD. Отрезок MN является средней линией, значит, он параллелен ВС. Отрезок QР – средняя линия треугольника АВС и параллелен ВС. По теореме о параллельности трех прямых, MN параллельно QР.
2)МР – средняя линия треугольника DВА, МР параллельно DА. Отрезок NQ – средняя линия треугольника АСD, NQ параллелен DА. Значит, МР параллельно NQ.
3)В четырехугольнике MNQP противоположные стороны попарно параллельны, значит, MNQP – параллелограмм.
4)Периметр параллелограмма MNQP равен удвоенной сумме смежных сторон. Длины этих сторон найдем как длины средних линий, равных половине параллельных сторон треугольника. MN равен половине ВС, 14:2 =7см, МР равен половине DА, то есть 6 см. В результате периметр равен 26 см. Задача решена.
Треугольники АВС и ABD не лежат в одно плоскости. Докажите, что любая прямая, параллельная отрезку СD, пресекает плоскости данных треугольников
Запишем условие и построим чертеж задачи.
Решение
Так по условию точка С принадлежит плоскости АВС а точка Д принадлежит плоскости АВД, то прямая СД пересекает плоскость АВС в точке С, а плоскость АВД в точке Д.
Тогда по лемме о пересечении плоскости параллельными прямыми имеем что люба прямая параллельная АД пересекает плоскость треугольника АВС и плоскость треугольника АВД.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 19771 |
| Номер материала | 919 |