
Урок "Параллелограмм"

Краткое описание документа:
Видеоурок по геометрии для 8-го класса поможет учащимся разобраться в освоении новой темы «Параллелограмм». Для изучения урока необходимо вспомнить свойства накрест лежащих углов; условия, при которых треугольники будут равными.
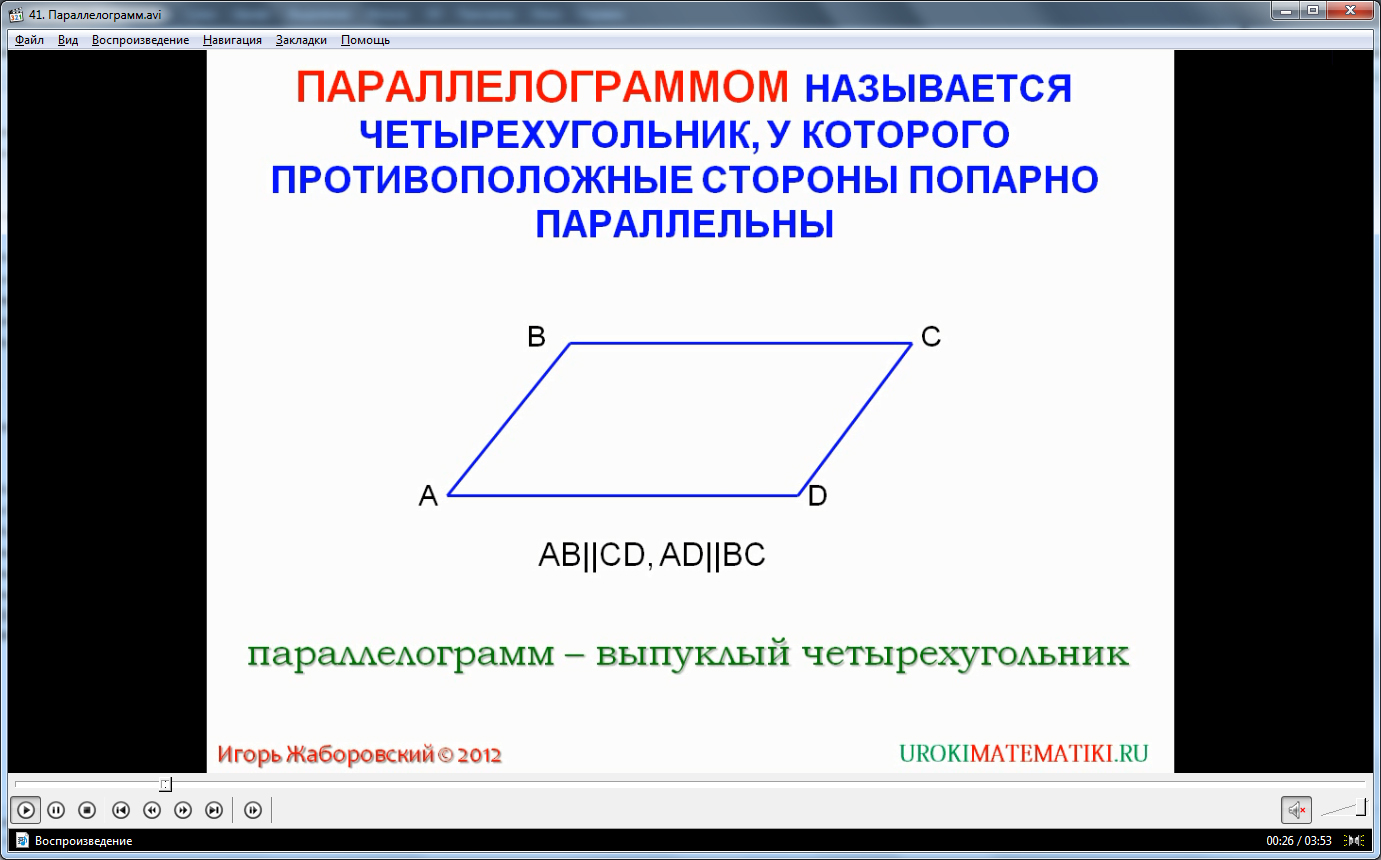
Дадим сначала определение параллелограмму. Это четырехугольник, у которого противоположные стороны параллельны попарно. На рисунке в видеоуроке вы можете увидеть изображенную фигуру – параллелограмм ABCD, в нем параллельны стороны ABи CD, и также ADи BC. Параллелограмм – это выпуклый четырехугольник.
Параллелограмм обладает следующими свойствами.
Первое свойство. У параллелограмма противоположные углы равны между собой и противоположные стороны равны. Рассмотрим доказательство. Посмотрим на рисунок, на котором изображен параллелограмм ABCD. Он разделен диагональю AC, которая делит фигуру на два треугольника ABCи ACD. Эти треугольники имеют одну общую сторону AC. Два прилежащих угла BAC (1) и ACD (2) равны, т.к. являются накрест лежащими углами при пересечении параллельных прямых ABи CDсекущей AC(параллельность сторон нам известна из определения параллелограмма). Аналогично два прилежащих угла CAD (3) и ACB (4) равны, они также являются накрест лежащими углами при пересечении параллельных прямых ADи BCсекущей AC. Таким образом, треугольники ABCи ACD равны, т.к. у них равна одна сторон и два прилежащих к ней угла. Т.к. треугольники равны, то отрезок ABравен отрезку CD, а отрезок ADравен отрезку BC; угол Bравен углу D.

Зная, что угол 1 (BAC) равен углу 2 (ACD), а угол 3 (CAD) равен углу 4 (ACB), запишем: угол А равен сумме углов 1 и 3, или сумме углов 2 и 4. А сумма углов 2 и 4 – это угол С. Т.е. угол А равен углу С.

Второе свойство. Точка пересечения диагоналей параллелограмма делит диагонали на равные отрезки. Докажем это утверждение. Начертим параллелограмм ABCD. Проведем диагонали AC и BD, обозначим точку пересечения диагоналей как О. Как следует из определения параллелограмма, сторона ABравна CD. Угол 1 (ABC) равен углу 2 (ACD), т.к.это накрест лежащие углы при пересечении секущей ACпараллельных прямых ABи CD. Угол 3 (ABD) равен углу 4 (BDC), это накрест лежащие углы при пересечении секущей BDпараллельных прямых ADи BC. Следовательно, треугольники AOBи COD равны, т.к. у них равна одна сторона и два прилежащих к ней угла. Равенство треугольников позволяет сделать вывод, что отрезки AOи OC равны, OBи OD также равны. Свойство доказано.

В видеоуроке мы ознакомились с понятием параллелограмма, подробно рассмотрели и доказали два свойства параллелограмма. Эти видеоматериалы могут быть с успехом применены учителем при проведении урока, т.к. наглядно и последовательно продемонстрируют все положения изучаемой темы.
Учащиеся при необходимости могут ознакомиться с темой «Параллелограмм» самостоятельно с помощью данного видеоурока.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5544 |
| Номер материала | 579 |