
Урок «Пирамида»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем знакомство с многогранниками. Вы уже знаете, что призмой называется многогранник, основания которого лежат на параллельных плоскостях, а боковые грани представляют собой параллелограммы.
Мысленно соединим вершины основания призмы с какой-либо точкой Р, принадлежащей другому основанию.
Мы получили новый вид многогранника, который называется пирамидой.
Итак, многогранник составленный из к- треугольников и к-угольника, называется пирамидой. Причём, многоугольник ABCDEF называется основанием, точка Р-вершиной, а треугольники, образованные отрезками РА, РВ, РС,РD, РЕ, РF-боковыми гранями, соответственно сами отрезки называются боковыми рёбрами.
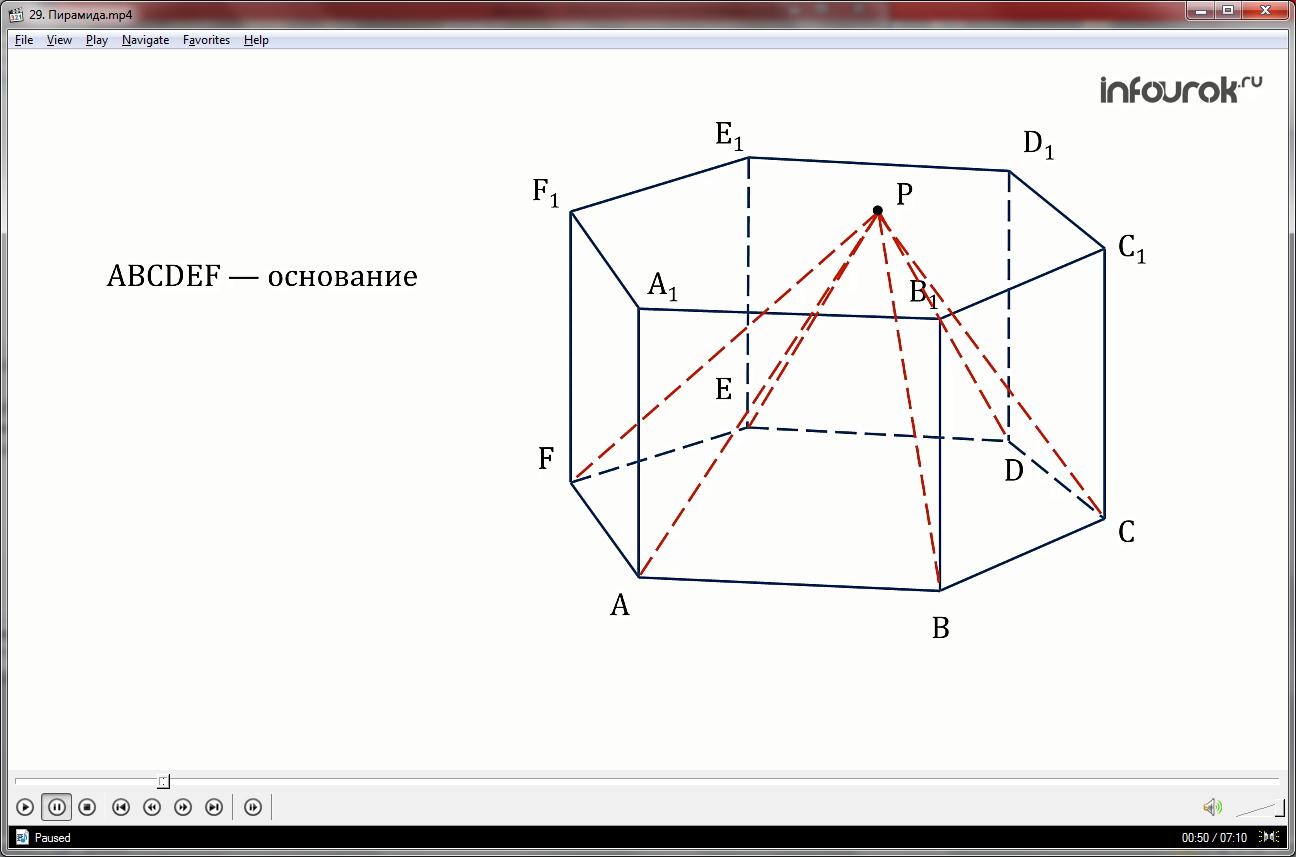
Принято называть пирамиду, начиная с вершины- так, наша пирамида называется РABCDEF.
Очевидно, что треугольная пирамида-это тетраэдр.
Так же существуют пирамиды, в основаниях которых лежат четырёхугольники, пятиугольники , а так же другие многоугольники.
Высотой пирамиды называется перпендикуляр, опущенный из её вершины к основанию.
В пирамидах SABCD и SABCDE высотой является отрезок SO.
Сумма площадей боковых граней пирамиды называется площадью её боковой поверхности, соответственно сумма площадей всех её граней (и основания и боковых граней), называется площадью полной поверхности пирамиды.
А сейчас решим задачу, применяя полученные новые знания.
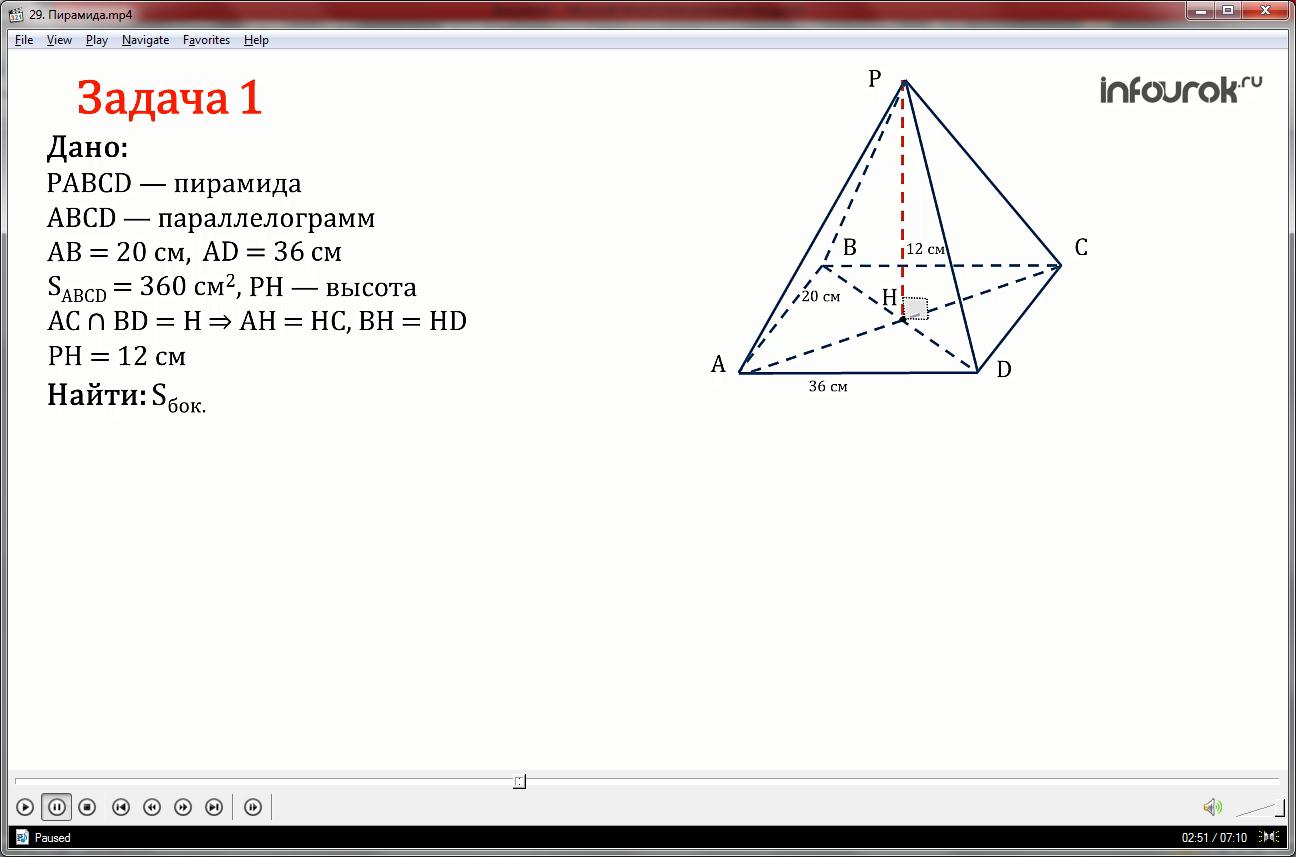
Задача 1.
Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, его площадь равна 360 см2.Найти площадь боковой поверхности пирамиды, если её высота проходит через точку пересечения диагоналей и равна 12 см.
Прежде чем приступить к нахождению площади боковой поверхности данной пирамиды, подумайте, можно ли сразу решить эту задачу? (пауза).
Вы уже знаете, что площадь боковой поверхности пирамиды равна сумме площадей её боковых граней. Поэтому нам необходимо найти площади четырех треугольников: АВР, ВРС,ДРС и АРД.
Решение:
1.Рассмотрим треугольники АВР и ДРС: АВ=ДС как противоположные стороны параллелограмма АВСД.
ВН и НД являются проекциями сторон ВР и РД на плоскость АВСД, вместе с тем ВН = НД, так как диагонали параллелограмма точкой пересечения делятся пополам. Из данного равенства мы можем сделать вывод, что РД=РВ (если проекции, проведённые из одной точки равны, то и наклонные равны).Аналогично доказывается равенство сторон АР и РС. Исходя из доказанного делаем вывод: Треугольники АВР и ДРС имеют по три равных стороны, следовательно они равны по третьему признаку равенства треугольников.

2. Рассмотрим треугольники ВРС и АРД: ВС=АД как противоположные стороны параллелограмма АВСД.
ВН и НД являются проекциями сторон ВР и РД на плоскость АВСД, вместе с тем ВН = НД, так как диагонали параллелограмма точкой пересечения делятся пополам. Из данного равенства мы можем сделать вывод, что РД=РВ (если проекции, проведённые из одной точки равны, то и наклонные равны).Аналогично доказывается равенство сторон АР и РС. Исходя из доказанного делаем вывод: Треугольники ВРС и АРД имеют по три равных стороны, следовательно они равны по третьему признаку равенства треугольников.
Теперь нам достаточно определить лишь площади треугольников APD и DPC.Найдём эти площади.
3.Дополнительное построение: проведём HQ перпендикулярно CD и HM перпендикулярно AD.
По теореме о трёх перпендикулярах PQ перпендикулярен CD и PM перпендикулярен AD.
Затем достроим отрезок HQ до пересечения со стороной АВ-получим точку Ф.
Точно так же продолжим отрезок МН до пересечения со стороной ВС-получим точку К.
Таким образом мы получили две высоты параллелограмма АВСД: FQ и MK.Зная площадь этого параллелограмма и его основания мы можем найти эти высоты.
FQ= = =18 см
МК= = =10 см
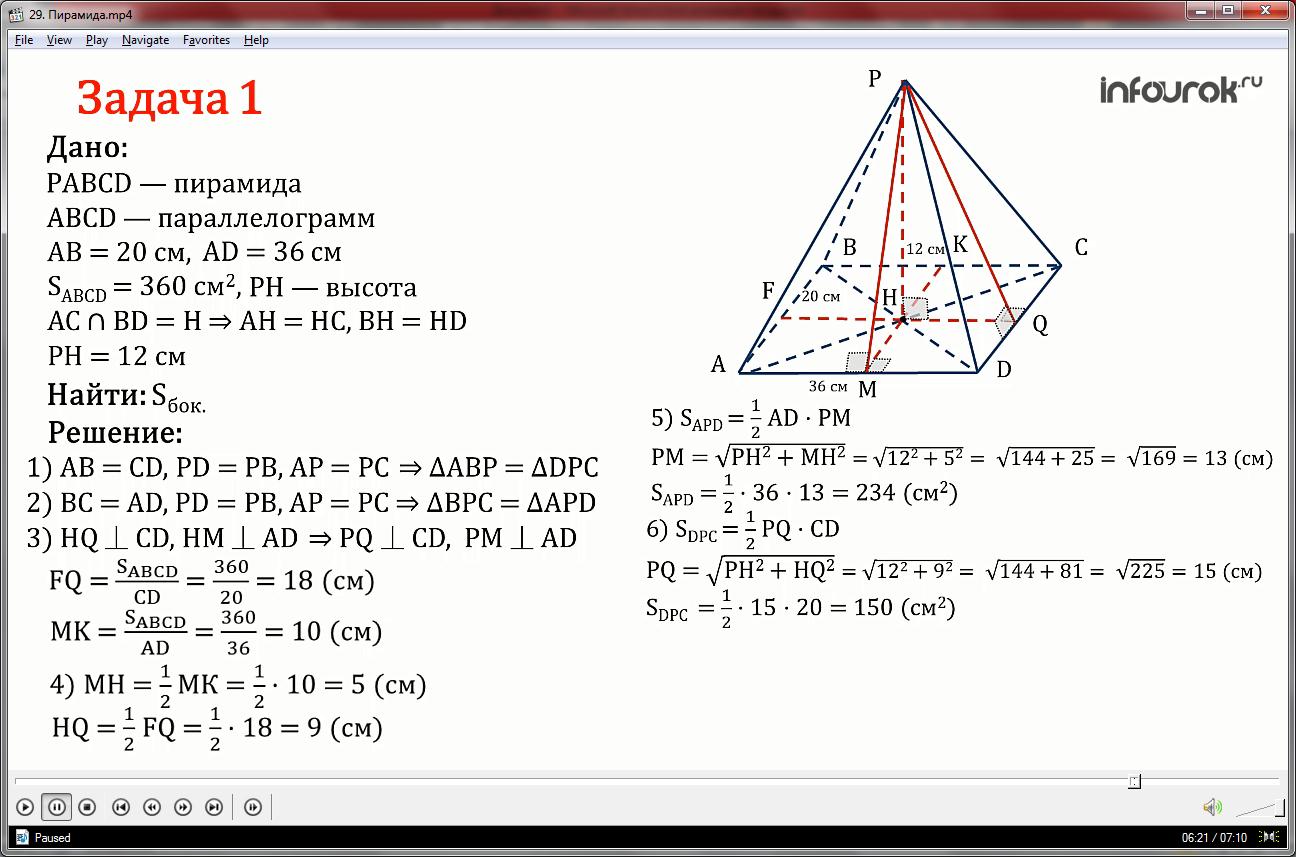
4. Отрезок МН равен половине высоты МК:
МН= МК= *10=5 см
Отрезок HQ равен половине высоты FQ:
HQ= FQ= *18=9 см
5.Найдем площадь треугольника АРД как половину произведения АД и РМ.
SAPD= AD*PM= *36*13=234см2
РМ в свою очередь найдем из прямоугольного треугольника РНМ по теореме Пифагора: PM=√PH2+MН2=√122+52=√144+25 =√169=13 см
6.Аналогичным образом найдём площадь треугольника ДРС:
SDPC= PQ*DC= *15*20=150см2
Длину PQ найдем из прямоугольного треугольника PHQ
По теореме Пифагора:
PQ=√PH2+HQ2=√122+92=√144+81=√225=15см
7.Теперь мы можем приступить к нахождению боковой площади пирамиды РABCD:
Sбок=SAPD+SABP+SBPC+SDPC
Ранее мы доказали ,что треугольники АВР и ДРС, а так же треугольники ВРС и АРД равны, поэтому
Sбок =2(SAPD+ SDPC)=2(234+150)=2*384=768см2
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 10114 |
| Номер материала | 943 |