
Урок "Площадь квадрата"

Краткое описание документа:
От множества геометрических фигур квадрат отличается тем, что является правильным четырехугольником с равными углами и равными сторонами. Если выразить сторону квадрата каким-нибудь числом, то можно найти площадь квадрата. Она численно равна квадрату его стороны.
S = a2.
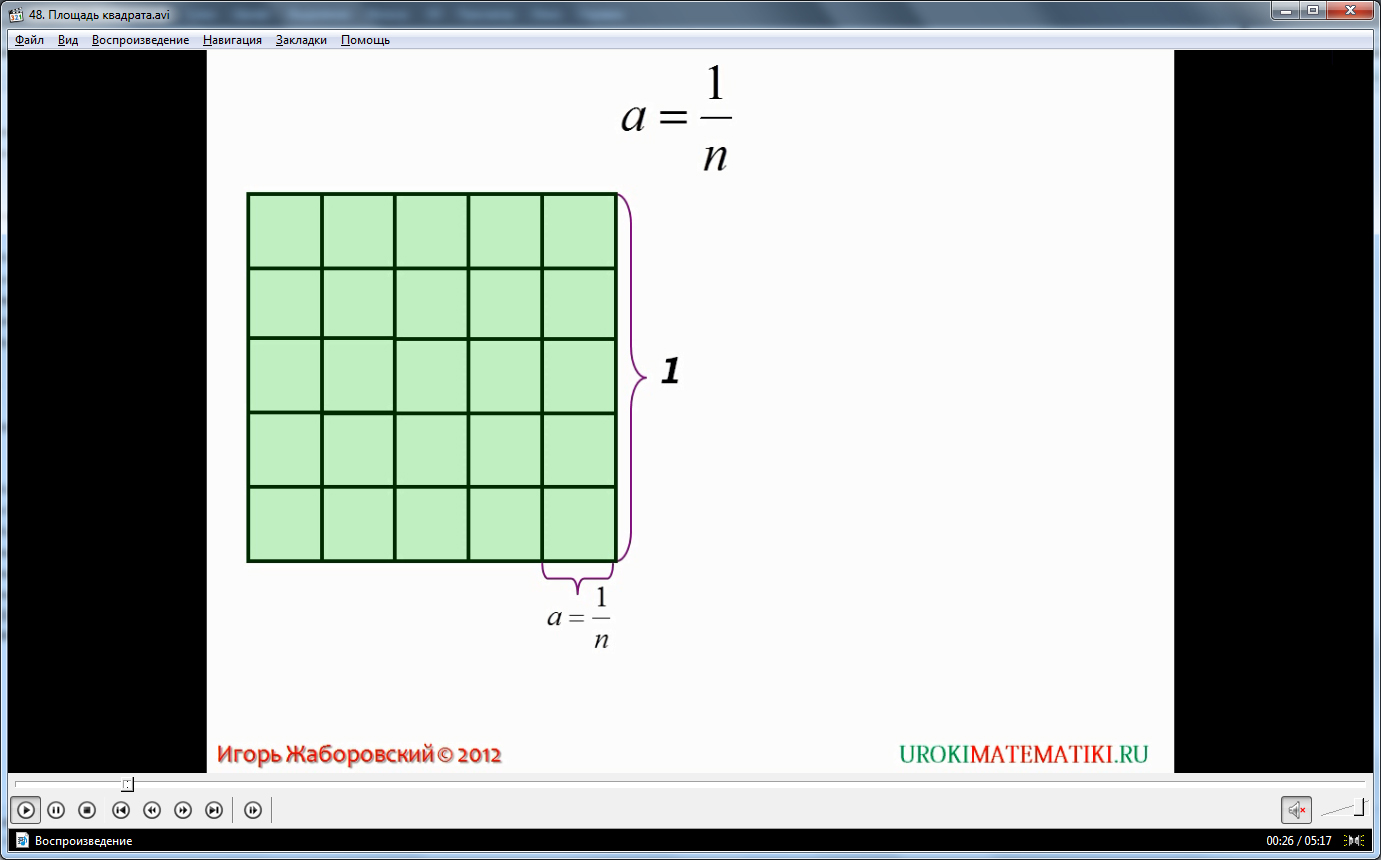
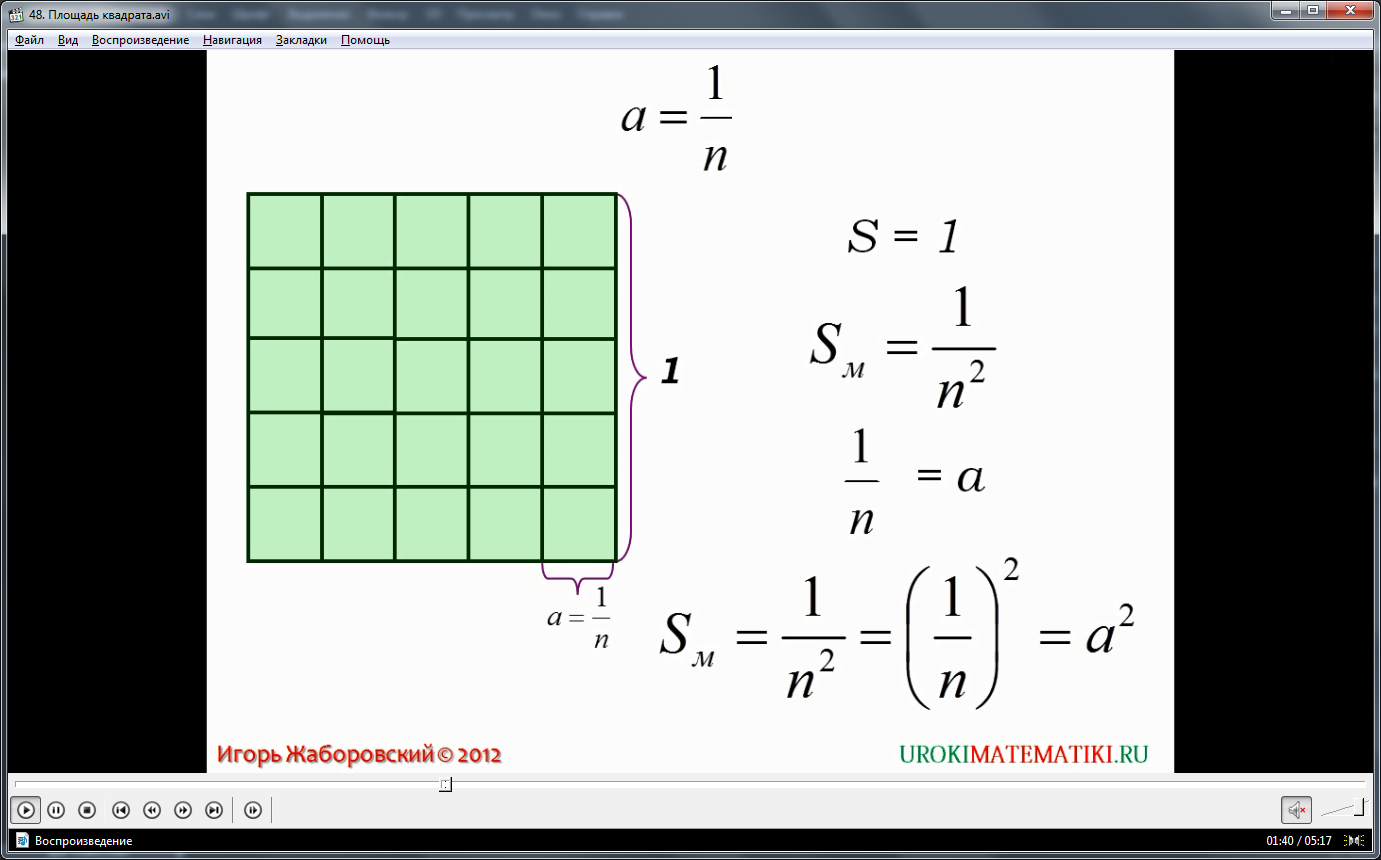
Доказательство этого положения приведено в данном видео уроке. На первом слайде показан квадрат. Его сторона принята равной единице. Следовательно, площадь квадрата тоже равна единице. Стороны квадрата разбиты одинаковые отрезки. На каждой стороне помещается одинаковое, причем целое, число отрезков. Это число в общем случае равно n. Итак, n – целое число. Если соединить отрезки, как показано на рисунке видео урока, квадрат окажется разделенным на маленькие квадраты. Всего их будет n2. В видео уроке сторона малого квадрата обозначена как a. Значит, ее длина равна 1/n, площадь же малого квадрата оказывается равной 1/n2. Площадь малого квадрата обозначена Sм. Поскольку дробь 1/n2 = (1/n)2, то можно записать, что Sм = (1/n)2. Но поскольку 1/n = a, можно записать, что Sм = a2.
Итак, был рассмотрен случай, когда n является целым числом.
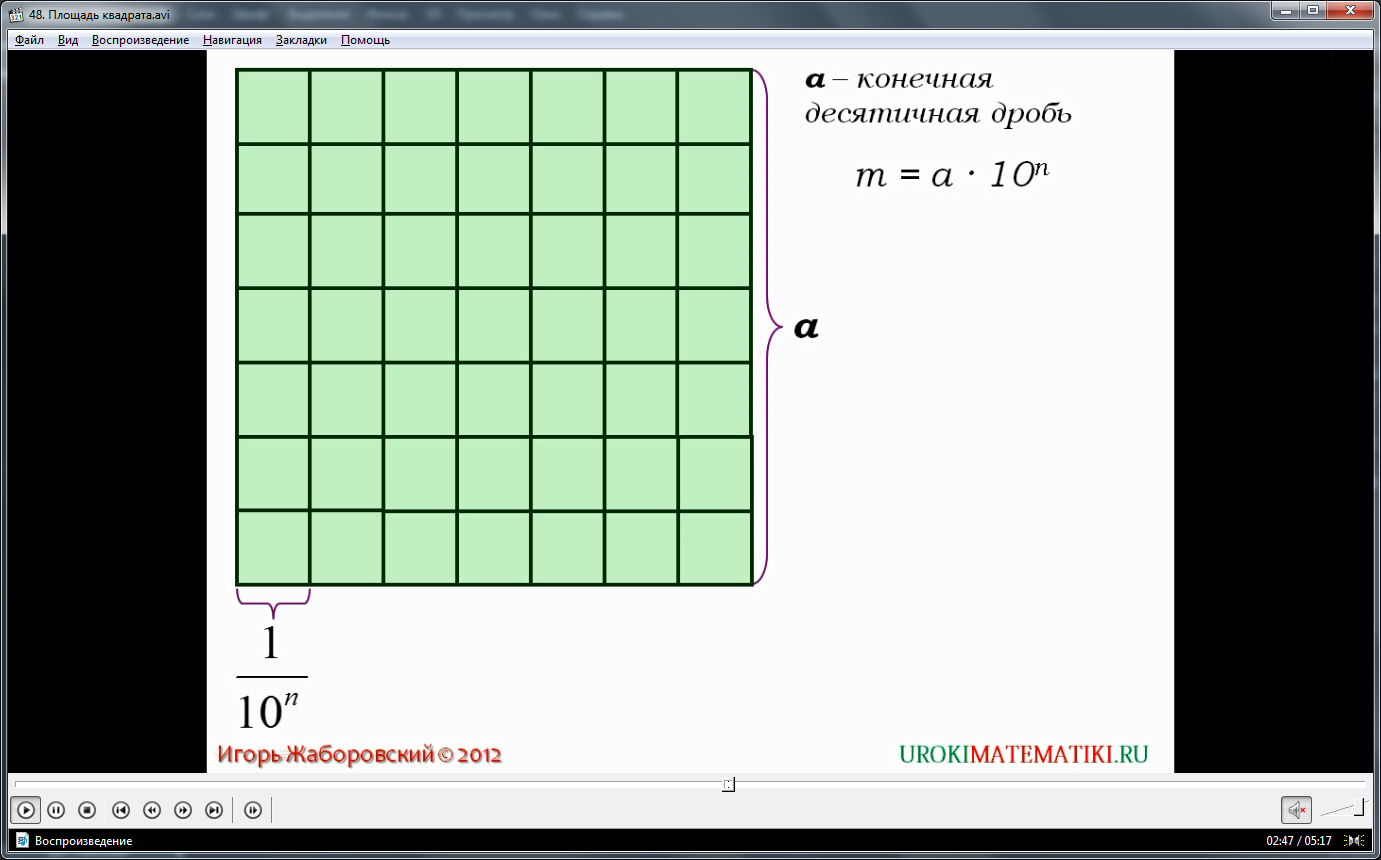
Следующий слайд видео урока объясняет случай, когда сторона квадрата a выражена конечной десятичной дробью. У этой дроби имеется после запятой n знаков. Стороны квадрата, показанного на слайде, разбиты на целое число равных отрезков. Это число обозначено m, и оно равно m = a х 10n. Сам же квадрат на слайде разбит также на целое число равных малых квадратов. Всего этих малых квадратов получается m2. Сторона каждого такого маленького квадрата равна числу a, деленному на число m.
Математическая запись будет выглядеть так:
a/m = a/a х 10n = 1/10n. Значит, длина стороны маленького квадрата равна 1/10n. Так и показано на слайде видеоурока.
Согласно тому, что было записано выше, площадь маленького квадрата должна равняться квадрату его стороны. На слайде видеоурока эта площадь найдена и записана так:
Sм = (1/ 10n)2. Но поскольку большой квадрат изначально был разбит на m2 равных частей, то общая площадь его, S, будет равна сумме площадей маленьких квадратов. Как известно, операцию сложения, если слагаемые одинаковы, можно заменить операцией умножения, и записать так:
S = m2 х (1/ 10n)2 = (m х 1/ 10n)2 = (a х 10n/10n)2 = a2.
Итак, в видеоматериале доказано, что если сторона квадрата выражена числом, представляющем собой конечную десятичную дробь, площадь этого квадрата будет определена квадратом этой стороны.
На последнем слайде этого видео урока рассматривается случай, когда сторона квадрата a выражена бесконечной десятичной дробью. Здесь предлагается рассмотреть некоторое число an, которое получится, если у числа a после запятой отбросить все десятичные знаки, начиная с n+1-го знака. Соотношение между числами a, an и an+1/10n записано в видеоматериале с помощью двойного неравенства.

Все части этого неравенства можно возвести в квадрат, тогда получается, что площадь исходного квадрата, S, больше, чем площадь квадрата со стороной an, и меньше, чем площадь квадрата со стороной an+1/10n. Это числовое неравенство на слайде проиллюстрировано с помощью рисунка. Если теперь бесконечно увеличивать число n, число 1/10n будет неограниченно уменьшаться и, в конце концов, мало отличаться от нуля. Из записанных неравенств видно, что число S при бесконечном увеличении числа n будет равно a2, что и требовалось доказать.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9078 |
| Номер материала | 586 |