
Урок "Площадь параллелограмма"

Краткое описание документа:
Применение видеоуроков сегодня – это удобный способ представления информации. В частности, видеоматериалы будут актуальны, если речь идет об обучении по школьной программе алгебре и геометрии.
В данном видеоуроке для 8-го класса по геометрии автор предлагает продолжить изучение площадей плоских фигур и остановиться на теме «Площадь параллелограмма».
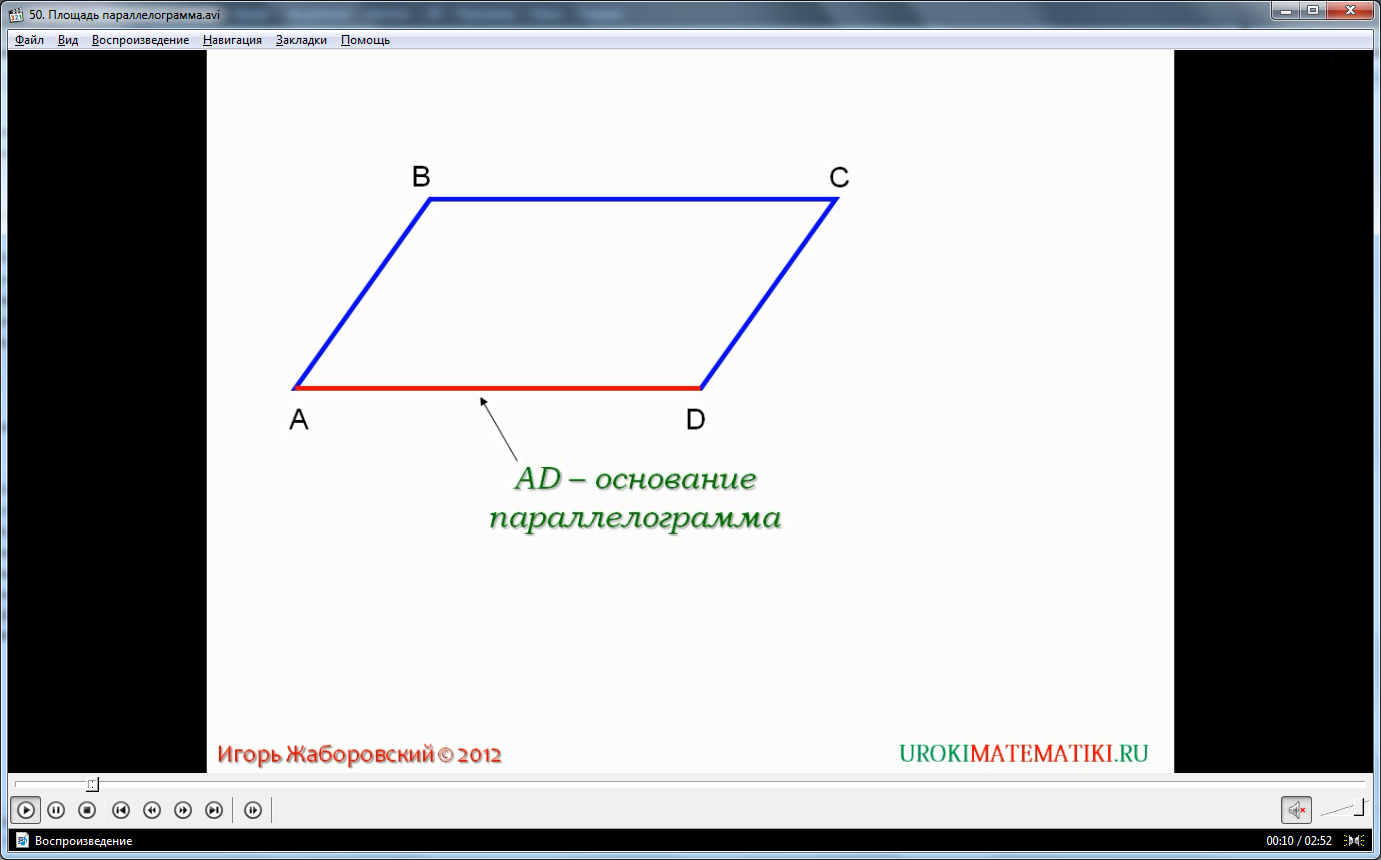
Урок начинается с того, что мы видим изображение параллелограмма на рисунке, фигура обозначена ABCD. Для удобства рассмотрения темы одну из сторон параллелограмма будем указывать как основание, а перпендикуляр, который проведен к основанию из точки на противоположной стороне, – высотой. Введем обозначения: AD– основание, BH – высота параллелограмма. Высота и основание указаны и выделены цветом на рисунке.

Далее автор приводит теорему. Площадь параллелограмма вычисляется путем умножения значений высоты и основания . Разберем доказательство. Допустим, дан параллелограмм. На рисунке он обозначен ABCD. Известно, что его площадь – это значение S. Будем считать, что сторона AD– основание параллелограмма. Проведем два перпендикуляра к основанию AD, на чертежеони обозначены BH и CK. Нам необходимо доказать, что значение Sравно произведению отрезков ADи BH. На первом этапе докажем, что площадь прямоугольника HBCKравна площади параллелограмма ABCD. Как видно по рисунку, треугольник KDCи параллелограмм ABCD – это составляющие одной фигуры, трапеции ABCK. Но также можно сказать, что трапеция ABCK состоит из двух других фигур: треугольника AHB и прямоугольника HBCK.
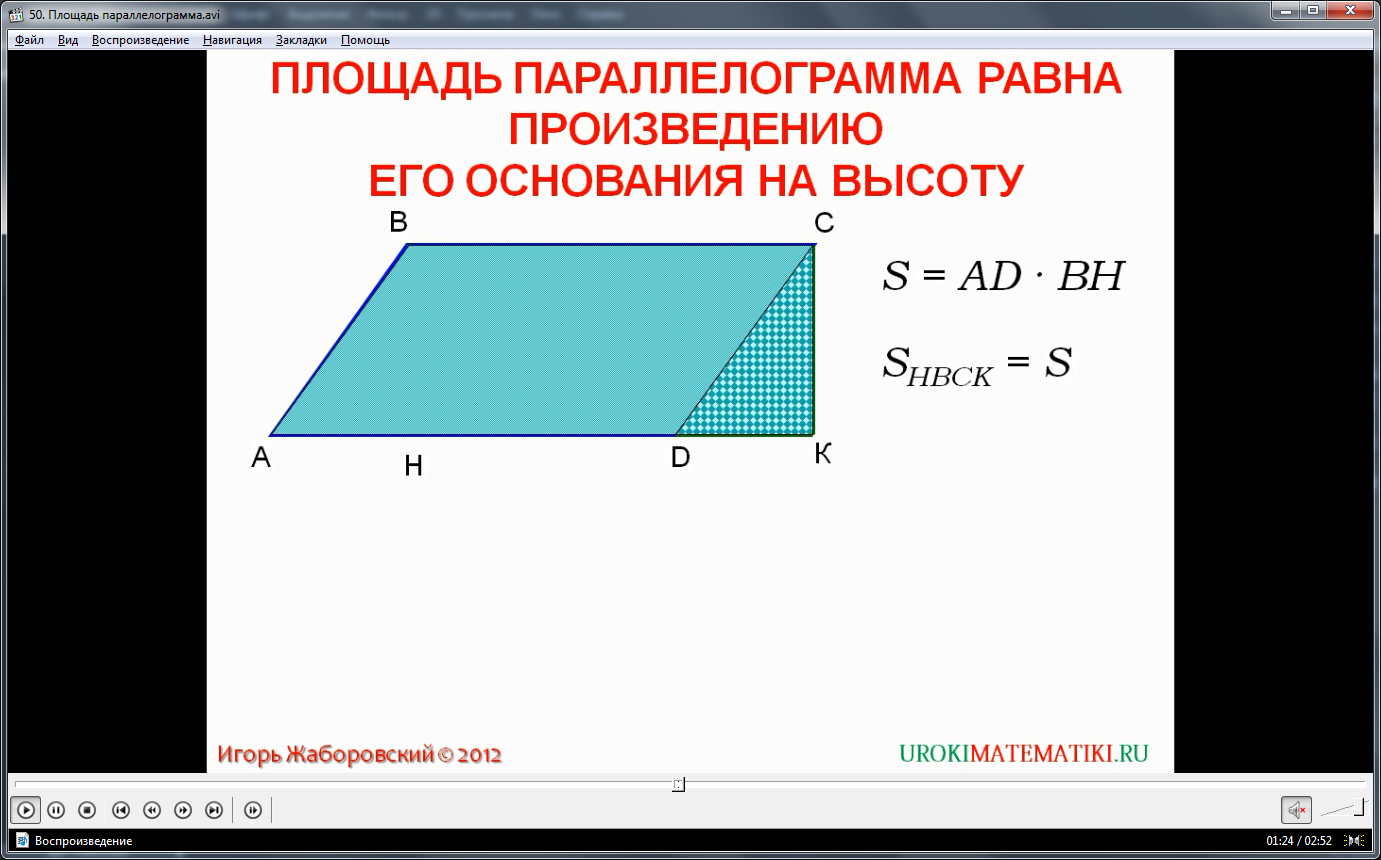
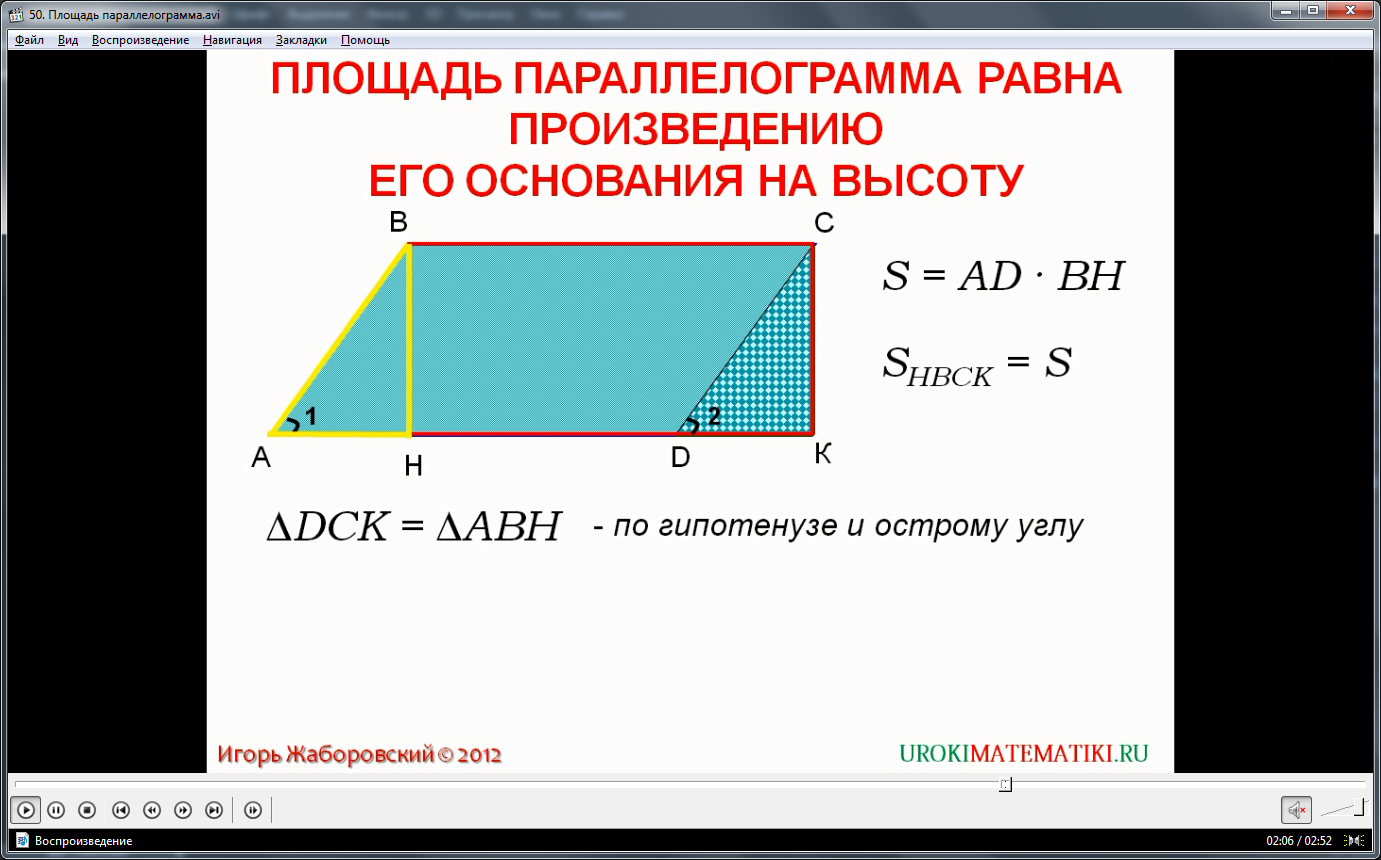
Отрезки ABи DC равны, т.к. это стороны параллелограмма, лежащие напротив друг друга. Углы 1 (BAH) и 2 (CDK) равны, это соответственные углы, которые образованы при пересечении секущей ADпараллельных прямых DC и AB. Углы BHAи CKDравны, т.к. BH и CK перпендикулярны AD. Значит треугольники KDCи AHBявляются прямоугольными. KDCи AHB–равные треугольники, в них выполняется равенство гипотенуз и одного острого угла. Из равенства треугольников следует, что площадь треугольника KDCравна площади треугольника AHB. Поэтому параллелограмм ABCDимеет такую же площадь, как и прямоугольник HBCK. Другими словами, SHBCK = S. Применим теорему о площади прямоугольника и запишем S = ВС xBH. Сторона CB равна стороне AD, т.к. это стороны параллелограмма, лежащие напротив друг друга. Следовательно, значение площади прямоугольника можно вычислить путем умножения стороны AD на сторону BH. Или S = ADxBH. Мы доказали теорему
Информация, изложенная в видеоуроке, поможет учителю при подготовке теоретической части урока, а также будет полезна ученикам, если они захотят освоить тему самостоятельно.
Важно хорошо разобрать и понять данный материал, т.к. эти теоретические положения будут использоваться в дальнейшем при решении задач.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5947 |
| Номер материала | 588 |