
Урок «Правильная пирамида»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
На прошлых занятиях вы уже познакомились с некоторыми видами многогранников -призмой и пирамидой.
Напомню, что многоугольник правильный, если его стороны равны и углы так же равны, а центр его лежит в центре вписанной или описанной окружности .
Поэтому пирамида называется правильной, если в её основании лежит правильный многоугольник.
Высотой правильной пирамиды называется отрезок, соединяющий центр основания с вершиной.
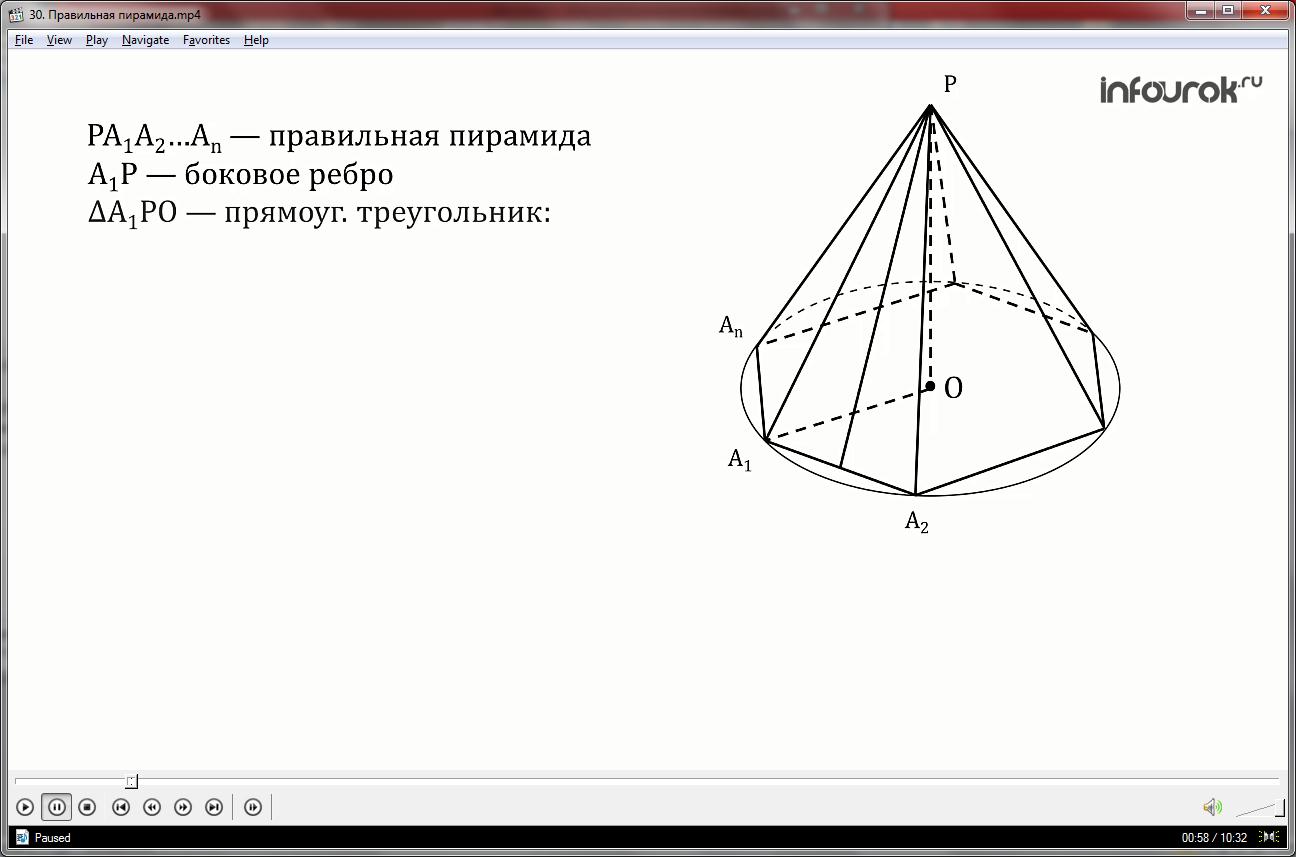
Рассмотрим правильную пирамиду PA1A2…An:
Любое боковое ребро (например А1Р) представляет собой гипотенузу прямоугольного треугольника (в нашем случае ΔА1РО), в котором катетами являются высота РО и радиус описанной окружности R. Выразим гипотенузу по теореме Пифагора: А1Р= . Аналогично можно выразить любое боковое ребро, таким образом мы доказали, что все боковые рёбра правильной пирамиды равны.
Исходя из вышеизложенного, очевидно, что боковые грани правильной пирамиды –равнобедренные треугольники. Так как в основании пирамиды лежит правильный многоугольник A1A2…An (а один, а два и так далее а энное), то основания всех треугольников будут равны, значит можно сделать вывод о том, что все боковые грани равны по третьему признаку равенства треугольников. Мы доказали, что боковые грани правильной пирамиды являются равными равнобедренными треугольниками.
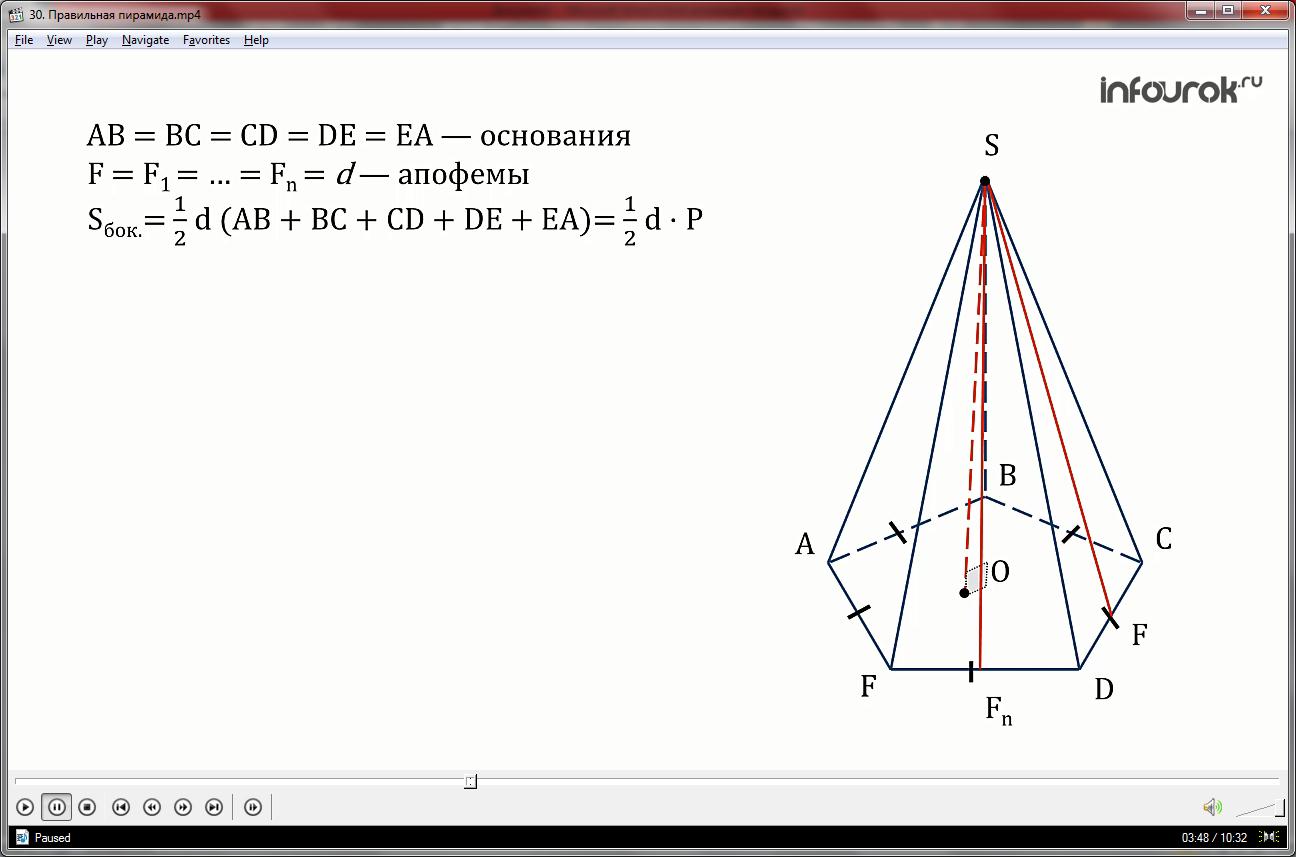
Проведём высоту в боковой грани SDC, отрезок
SF называется апофемой.
Очевидно, что все апофемы правильной пирамиды равны, а так же все двугранные углы при основании равны.
Так как в правильной пирамиде боковые грани равны и являются равнобедренными треугольниками, то получаем в пирамиде SABCDE, грани SAB, SBC, SCD, SDE, SAE, являются равнобедренными треугольниками которые равны, тогда высоты проведенные из вершин равнобедренных треугольников (то есть апофемы пирамиды) равны.
Рассмотрим треугольники SОМ и SОF они прямоугольные, так как SO–высота пирамиды, то есть перпендикулярна к основанию АВС,
Данные треугольники SОМ и SОF равны по гипотенузе и катету, из равенства треугольников получаем равенство углов SMO и SFO.
А данные углы являются линейные углами для двугранных углов SAEO и SCDO, тогда данные двугранные углы равны, аналогично рассматривая пары других двугранных углов, докажем что они равны.

Найдем площадь боковой поверхности правильной пирамиды.
Выше мы уже доказали, что боковые грани правильной пирамиды –это равные равнобедренные треугольники, основания которых-стороны основания пирамиды, а высоты–это апофемы. Площадь S боковой поверхности равна сумме боковых граней. Где площадь каждой боковой грани равна половине произведения основания на апофему. Вынесем общий множитель d за скобку, в скобках останется сумма сторон основания пирамиды, а это есть периметр основания.
Таким образом мы доказали теорему о том, что площадь боковой поверхности правильной пирамиды равна половине произведения апофемы на периметр основания.
Разберём несколько задач, применяя полученные знания.
Задача 1. (№257 учебника Атанасян 10-11 класс)
Боковое ребро правильной четырехугольной пирамиды образует угол в 60є с плоскостью основания. Найдите площадь поверхности пирамиды, если боковое ребро равно 12 см.
Решение.
1. Для того что бы найти площадь полной поверхности пирамиды нам необходимо вычислить площади всех боковых граней и её основания
2.SABC-правильная пирамида значит точка О-это центр квадрата АВСД.
Рассмотрим треугольник АSO (а эс о), он прямоугольный так как, СО высота пирамиды, угол меду боковым ребром и основание равен 60є, т.е. угол SAO равен 60є, а угол ASO равен 90є минус 60є равен 30є, следовательно получаем АО равно половине SA и равно 6 см., как катет лежащий против угла в 30 градусов.

3. треугольник ABO равнобедренный прямоугольный, так как диагонали квадрата перпендикулярны и точкой пересечения делятся пополам, боковые стороны треугольника равны 6 см . Тогда применяя теорему Пифагора найдем гипотенузу треугольника АВ равно корню квадратному из суммы квадратов катетов и равно 6корней из 2двух см.
Зная сторону квадрата найдем площадь и периметр основания площадь равна квадрату стороны и равно 72 квадратных см.
Периметр равен 4 умножить на длину стороны и равен двадцать четыре корней из двух.
4. Найдем апофему пирамиды SH из прямоугольного треугольника ABO,
AH равна половине стороны квадрата т.е. равна шесть корней из двух см.
Найдем катет SH по теореме Пифагора равного корню квадратному из разности квадратов гипотенузы SA и катета AH, получаем SH ревен шесть корней из шести см.Вычислим площадь боковой поверхности как половина произведения половины апофемы на периметр получаем 144корней из трех кв.см.
5. Вычисляем площадь поверхности пирамиды она равна 72умножить на на сумму одного и двух коней из трех кв. см.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9920 |
| Номер материала | 944 |