
Урок «Правило параллелепипеда»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
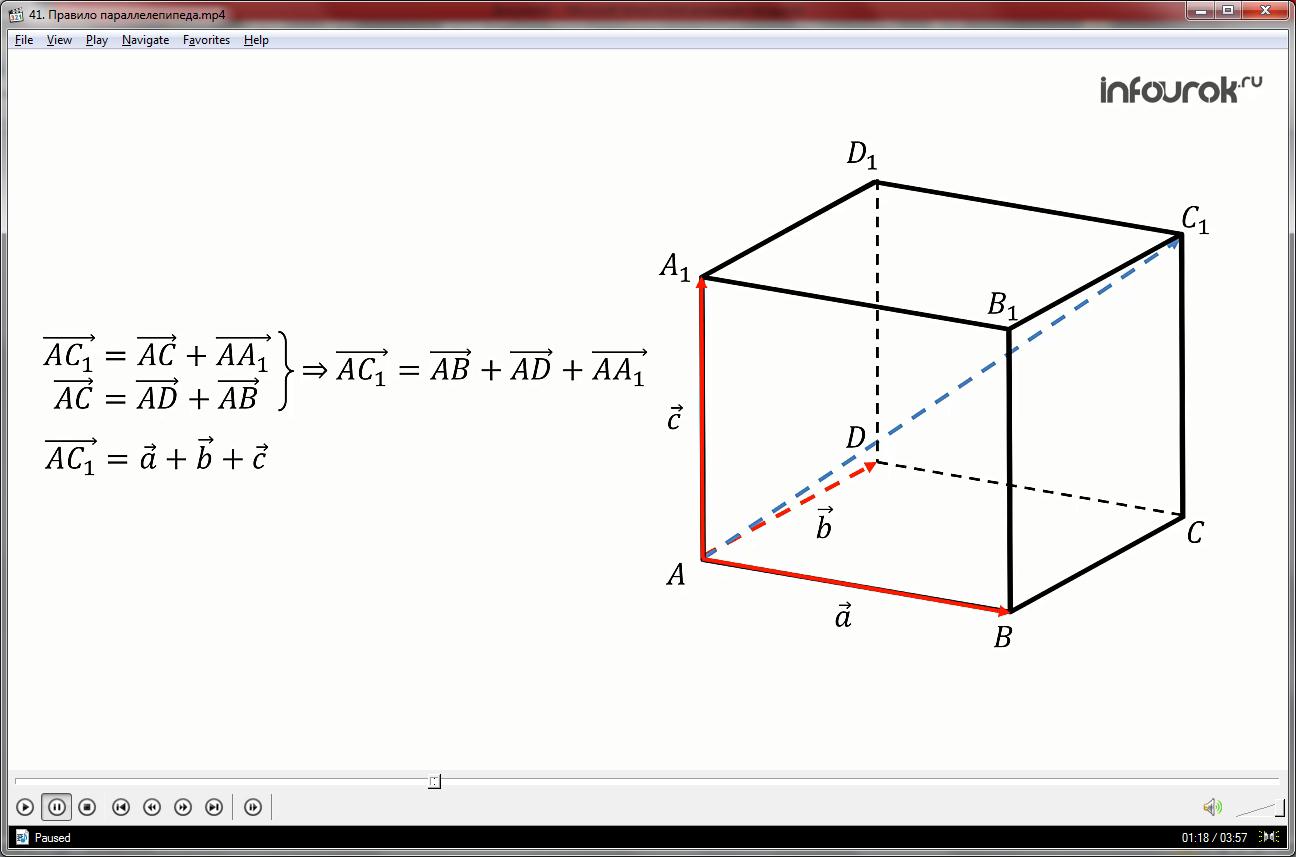
Сложение нескольких векторов в пространстве выполняется так: первый вектор складывается со вторым, затем их сумма – с третьим вектором и так далее. Это правило нам известно как правило многоугольника. На рисунке показано сложение трех векторов в пространстве.
От точки О отложен вектор ОА равный вектору а, затем от точки А вектор АВ равный бэ, от точки В отложен следующий вектор ВС равный це, и соединяем первую и последнюю точки О с С получаем вектор ОС равный сумме векторов а, бэ и це.

Сформулируем правило многоугольника.
ЕслиА1, А2, А3 и так далее Аn – произвольные точки, то вектор А1А2 плюс вектор А2А3 плюс вектор А3А4 и так далее плюс Аn-1 An, то в результате получится вектор А1Аn.
На рисунке показана сумма шести векторов.
Если начало вектора совпадает с концом последнего, то сумма равна нулевому вектору.
Рассмотрим сумму векторов
Выполнив сложение по правилу многоугольника, получаем вектор АА или нулевой вектор.
Решим задачу №337 (в)
Упростите выражение

Решение: Заменим в выражении вычитание на сумму. Для этого заменим отрицательные векторы на противоположные. Вектор минус ВС равен вектору СВ, минус вектор РМ равен вектору МР. Минус вектор АР равен вектору РА. Вектор АС в сумме с вектором СВ дают вектор АВ. Векторы МР и РА дают вектор МА. Затем, складывая векторы АВ и ВМ, получаем вектор АМ. В итоге сумма векторов АМ и МА дают нулевой вектор. Выражение упрощено.
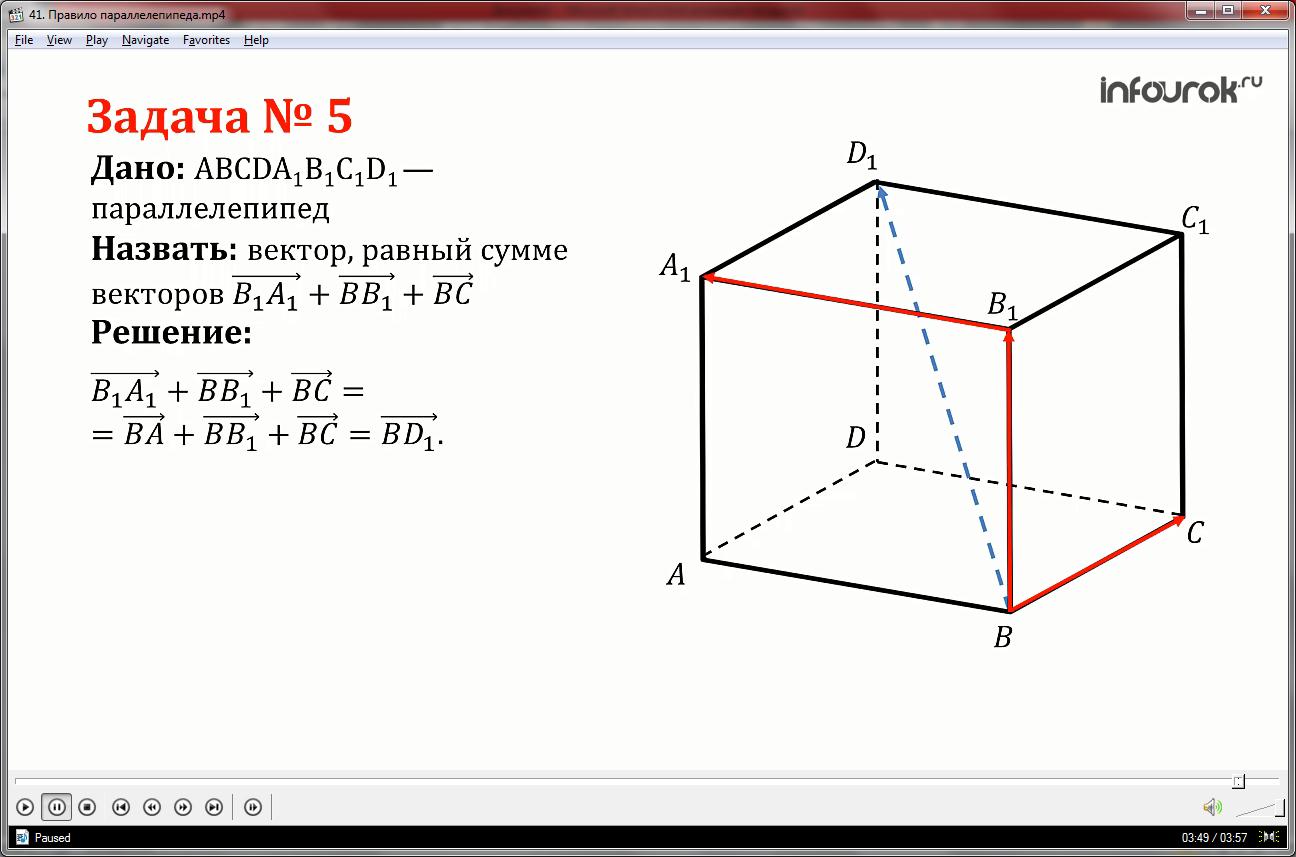
Решим задачу на доказательство №338.
Дан параллелепипед АВСDA1B1C1D1. Докажите, что , где О – произвольная точка пространства.
Доказательство. Преобразуем левую часть равенства. Вектор ОА представим как сумму векторов ОА1 и А1А по правилу треугольника. Вектор А1А равен вектору С1С как противоположные ребра параллелепипеда. Складывая векторы ОС1 и С1С, получаем ОС. В результате преобразований получили правую часть равенства. Доказательство окончено.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11084 |
| Номер материала | 955 |