
Урок "Примеры задач на построение"

Краткое описание документа:
Продолжая осваивать решение задач на построение, необходимо детально изучить основные способы решения различных задач. Видеоурок «Примеры задач на построение» направлен на формирование одних из наиболее важных в геометрии навыков – проведение корректных построений и поиск решения геометрических задач при помощи построения.
Демонстрация решения задач в виде видеоурока дает возможность наглядно представить ученикам решения, отметить основные сложности и особенности решения таких задач. Выделение цветом помогает определить важные детали, запоминание которых поможет быстрее освоить данный способ построения. На первый взгляд такие задачи не решаются при помощи обычной линейки и циркуля, но зная особенности таких построений, можно освоить этот важный способ решения задач на построение.
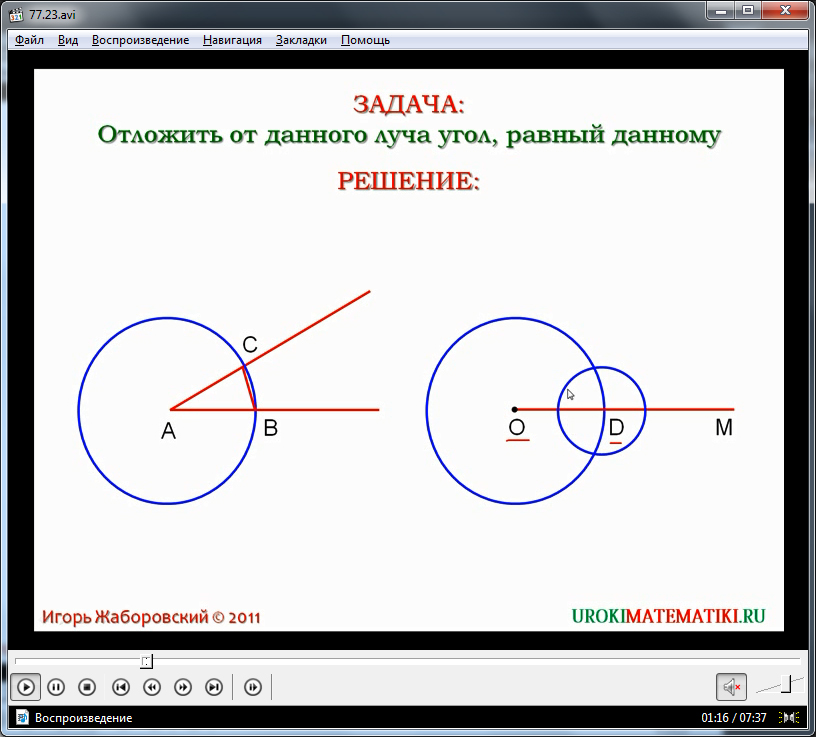
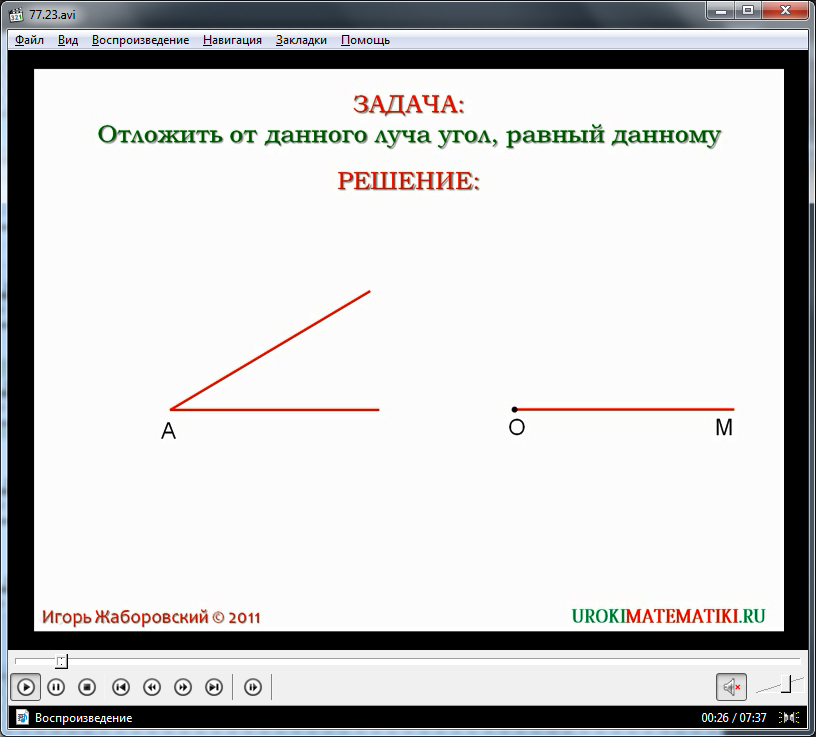
- Первый пример задачи, решаемой при помощи обычной линейки и циркуля – построение угла, который равен данному. На экране выводится условие задачи. Решение начинается с изображения луча ОМ и угла ∠А. Разъясняется, что условие задачи означает, что необходимо построить угол, равный построенному углу ∠А так, чтобы одной из сторон полученного угла стал луч ОМ. Для решения данной задач предлагается сначала провести окружность некоторого радиуса с центром в точке А. Отмечаются точки пересечения В и С данной окружности с лучами угла ∠А. Затем такая же окружность проводится с центром в начале луча ОМ. Отмечается пересечение окружности с лучом в точке D. Далее необходимо циркулем отмерить расстояние между точками В и С, принадлежащие углу ∠А, и построить окружность измеренного радиуса, где центр в точке D. Для дальнейшего построения обращается внимание ученика на точки пересечения данной построенной окружности с первой окружностью. Одну из точек пересечения отмечаем как точку Е. По построению угол ∠МОЕ является углом, равным углу ∠А.
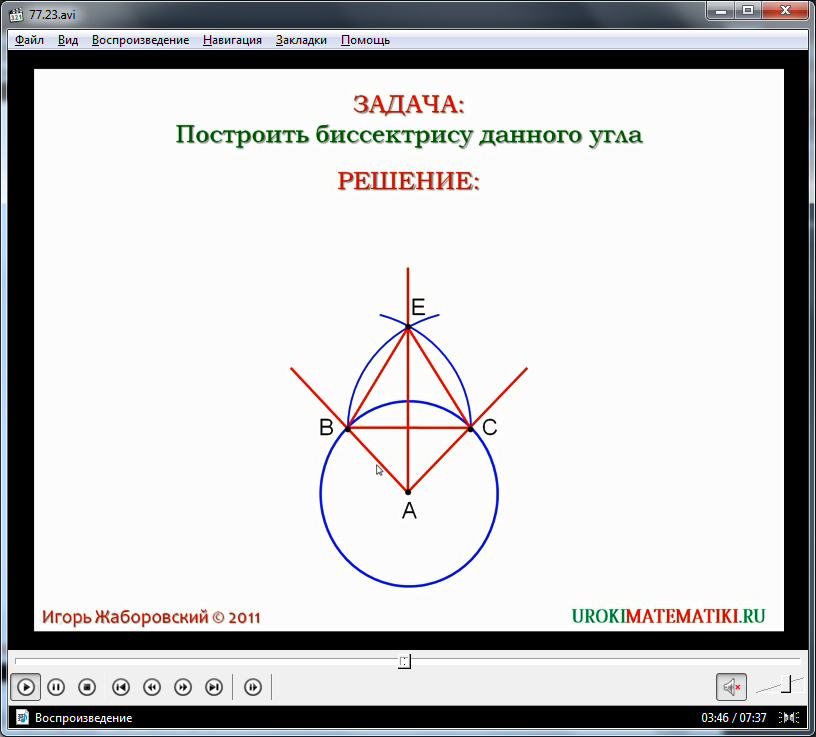
Приводится доказательство данного факта на основе имеющихся знаний по признакам равенства треугольников. Для доказательства равенства углов необходимо рассмотреть треугольники ΔАВС и ΔОDE. Равенство сторон АВ=ОD и АС=ОЕ следует из построения, так как они являются радиусами одинаковых окружностей. При этом СВ=ED по построению малой окружности, так как ее радиус был взят равным СВ. Используя третий признак равенства треугольников, утверждаем, что данные треугольники равны. А соответствующие углы равных треугольников попарно равны, поэтому равенство ∠А=∠МОЕ верно. При помощи линейки и циркуля построен угол, равный данному. Также отмечается, что при решении практических задач на местности таким способом можно было бы построить угол, равный данному при помощи веревки. - Второй пример задачи – построение биссектрисы угла. Условие задачи отображается на экране. При решении для начала изображается угол ∠ВАС. От центра данного угла откладывается окружность произвольного радиуса. Отмечаются точки пересечения данной окружности с точками, принадлежащими сторонам угла ∠ВАС. Далее необходимо провести две окружности, центрами которых являются данные точки пересечения. Образуются две точки при пересечении построенных окружностей. Среди этих точек одна лежит внутри угла. Ее обозначаем, как точку Е. Чтобы найти эту точку, не обязательно изображать полностью эти окружности – достаточно прочертить части, в которых находится точка их пересечения, расположенная внутри угла. Это и сделано на демонстрируемом рисунке. Задача решена.
Теперь докажем, что результат построения – отрезок ОЕ - является биссектрисой угла. Чтобы доказать справедливость суждения, необходимо рассмотреть треугольники ΔАВЕ и ΔАСЕ. Данные треугольники равны по трем сторонам (по третьему признаку равенства треугольников). АВ=АС как радиусы построенной окружности, сторона АЕ является общей для двух треугольников, а ВЕСЕ по построению как радиусы одинаковых проведенных окружностей. У равных треугольников соответствующие стороны попарно равны. Это значит, что равны будут и углы ∠ВАЕ=∠САЕ. Следовательно, луч АЕ делит данный угол на две равные части и является его биссектрисой. Пример демонстрирует, что угол может быть разделен при помощи циркуля и линейки на две равные части. Таким же образом можно разделить угол и на четыре равные части, разделив его сначала пополам, а затем каждый из углов также разделить пополам.
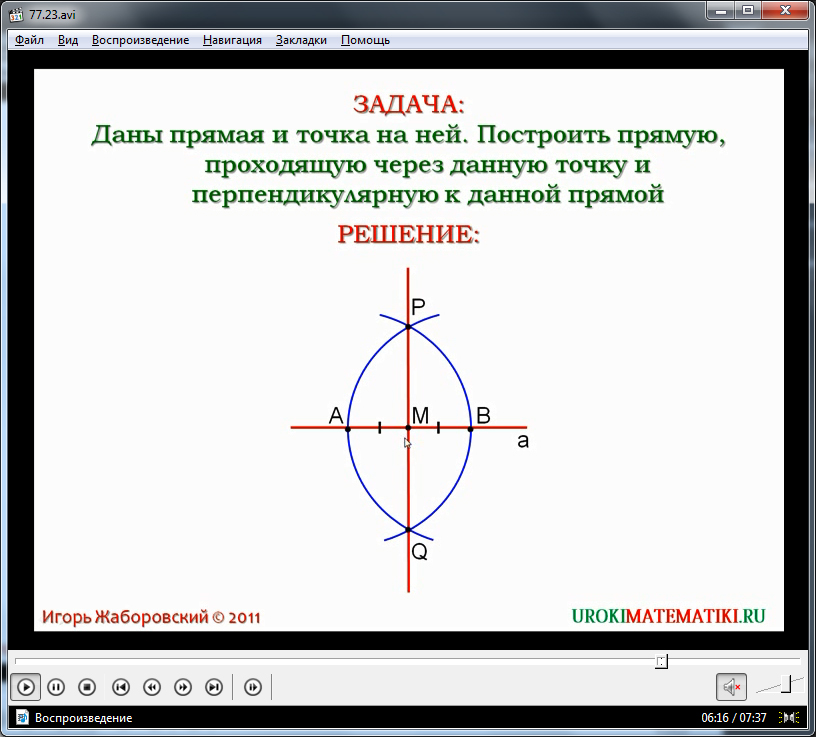
Материал дополняется интересными фактами, связанными с задачей трисекции угла. Ученики информируются о том, что при помощи линейки и циркуля разделить угол на три части невозможно. Доказательство данного утверждения было произведено в XIX веке. - Третий пример – построение перпендикулярных прямых. Условие к задаче отображается на экране. Для начала проводится прямая с отмеченной на ней точкой. Через данную точку необходимо провести прямую, перпендикулярную к данной. Ниже условия изображается прямая a с отмеченной точкой М. При помощи циркуля отметим равные отрезки на лучах МА и МВ. Далее необходимо провести две окружности с центрами в точках А и В. Отмечаются точки пересечения этих окружностей P и Q. Через данные точки проводится прямая. Эта прямая и будет искомой прямой, перпендикулярной а.
Докажем, что это утверждение верно. Для этого рассмотрим треугольник ΔРАВ. Данный треугольник является равнобедренным, так как его стороны РА и РВ равны по построению – они являются радиусами одинаковых окружностей. РМ – медиана указанного треугольника. А в равнобедренных треугольниках медиана также является и высотой – соответственно, она перпендикулярна АВ, а значит, и прямой а. - Четвертая задача – построение середины отрезка. На экране отображается условие задачи, после чего приводится требуемое построение. На прямой отмечен отрезок АВ, середину которого необходимо найти. Циркулем отмечаем радиус размером длины отрезка АВ и строим окружности с данным радиусом. Отмечаются точки пересечения окружностей – P и Q. После проведения прямой, соединяющей точки P и Q образуется точка О пересечения отрезка PQ и прямой. Данная точка и является серединой отрезка АВ.
Доказательство того, что О является серединой АВ, строится на равенстве треугольников ΔАРQ и ΔBPQ. Действительно, АР=РВ и АQ=QB как равные радиусы окружностей по построению. PQ – общая сторона треугольников. Из равенства треугольников следует равенство углов ∠ОРА=∠ОРВ. В равнобедренном треугольнике ΔАРВ биссектриса РО является также и медианой. Это означает, что отрезок АВ делится точкой О на две равные части, то есть О – середина отрезка.
Видеоурок «Примеры задач на построение» может быть использован учителем на уроке как средство наглядности при рассмотрении решения задач на построения. Также данный материал может быть использован в самостоятельном изучении материала и при дистанционном изучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7593 |
| Номер материала | 510 |