
Урок «Призма»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Продолжаем знакомство с многогранниками.
Многогранник – это поверхность, составленная из многоугольников и ограничивающая геометрическое тело.
Представим два равных между собой многоугольника, которые расположены в параллельных плоскостях и соединим соответственные вершины этих многоугольников. Видно, что получившиеся отрезки параллельны, а каждый из образовавшихся четырёхугольников является параллелограммом, так как имеют попарно параллельные противоположные стороны.
Такой многогранник, составленный из параллелограммов и двух равных многоугольников, расположенных в параллельных плоскостях называется призмой.
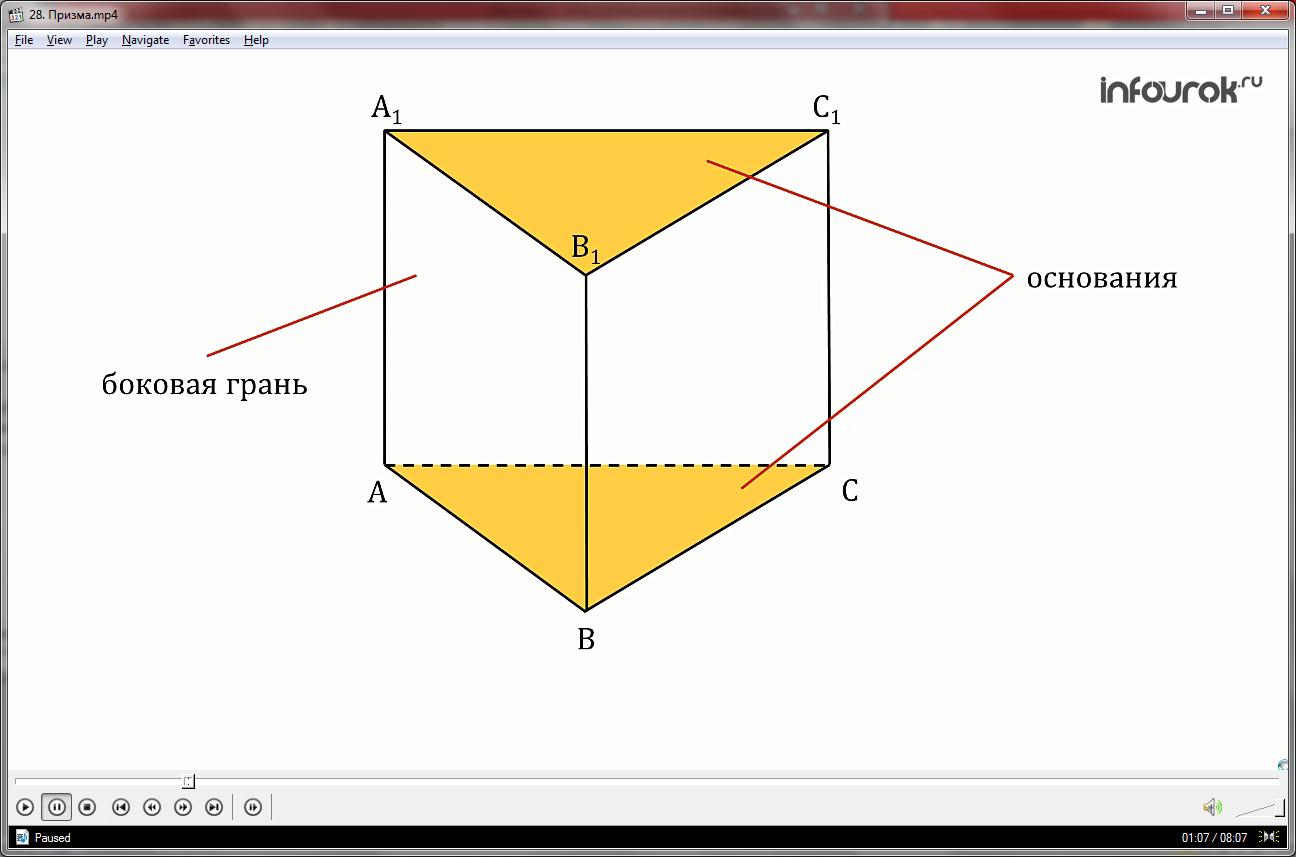
Равные многоугольники называют основаниями, а параллелограммы – боковыми гранями.
Отрезки, соединяющие соответственные вершины это боковые рёбра.
Если в основании призмы лежит треугольник, то призма называется треугольной.
Высотой призмы называется перпендикуляр, проведённый из любой точки основания к плоскости другого.
В случае, если боковые рёбра не перпендикулярны основаниям, то призма называется наклонной. В противоположном случае-прямой, в такой призме боковые рёбра будут одновременно и высотами.
Боковые грани прямой призмы являются прямоугольниками.
Боковые грани наклонной призмы являются параллелограммами.
Если в основании призмы лежит правильный многоугольник(стороны и углы равны), то призма называется правильной, в противном случае- неправильной.
Сумма площадей всех граней призмы называется площадью полной поверхности.
Сумма площадей только боковых граней призмы называется площадью боковой поверхности.
Несложно выяснить, что площадь полной поверхности равна сумме площадей боковой поверхности и площади оснований.
Боковыми гранями прямой призмы являются прямоугольники, поэтому площадь боковой поверхности равна сумме площадей этих прямоугольников.
Известно, что площадь прямоугольника равна произведению стороны а на высоту h.
Высоты h прямоугольников являются и высотами h призмы.
Вынесем общий множитель h за скобку, в скобке осталась сумма сторон а основания призмы.

Данная сумма это есть периметр основания.
Таким образом мы доказали теорему о том, что площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр её основания.
Задача 1.
В основания прямой призмы АВСА1 В1 С1 лежит прямоугольный треугольник АВС с прямым углом С.Через сторону ВС и вершину А1 проведена плоскость так, что угол ВА1 С равен 30 градусов, А1В равна 10, АС равна 5.Найти площадь боковой поверхности призмы.
Прежде чем приступить к решению задачи необходимо провести её краткий анализ:
площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр её основания,а это стороны: АС, ВС, АВ и высота АА1.Из условия известна длина только отрезка АС, поэтому прежде чем приступить к решению задачи, необходимо определить недостающие данные, а это ВС, АВ и АА1.

Решение:
1.По теореме о трёх перпендикулярах отрезок А1С перпендикулярен ВС, таким образом треугольник А1ВС прямоугольный.
2.Известно, что катет лежащий против угла в 30 градусов равен половине гипотенузы, значит катет ВС равен половине гипотенузы А1В, то есть равен 5.
3.Теперь нам известна сторона ВС равная 5, АС равна 5 по условию и мы можем найти АВ по теореме Пифагора из прямоугольного треугольника АВС:
АВ=√ВС2+АС2=√52+52=√50=5√2
4.Из прямоугольного треугольника А1 АВ так же по теореме Пифагора находим АА1:
АА1=√А1В2-АВ2=√100-50=5√2
5.Таким образом, все неизвестные величины найдены и мы можем приступить к нахождению площади боковой поверхности призмы
Sбок=АА1(АВ+ВС+АС)=5√2(5√2+5+5)=50+50√2
Общий множитель 50 можно вынести за скобку
Отсюда Sбок=50(1+√2)
Ответ: Sбок=50(1+√2)
Задача 2.
Диагональ правильной прямоугольной призмы наклонена к плоскости основания под углом 60 градусов. Найти площадь сечения, проходящего через противолежащую сторону верхнего основания и через сторону нижнего основания , если известно, что диагональ основания равна 4√2 см.
Решение:
1.Так как отрезок АВ перпендикулярен АД и В1В перпендикулярен АД, то по теореме о трёх перпендикулярах АВ1 перпендикулярен АД. Вместе с тем отрезок В1С1 параллелен АД, значит АВ1 перпендикулярен В1 С1, значит искомое сечение AB1C1D является прямоугольником.
Для того, что бы найти площадь сечения достаточно найти стороны АД и ДС1.
2.Пусть диагональ призмы d.Данный многогранник является прямоугольным параллелепипедом, диагонали которого равны, поэтому d=В1Д=АС1.
3.В основании лежит правильный четырёхугольник- квадрат, диагонали которого являются биссектрисами углов, значит угол АВД равен 45 градусов.
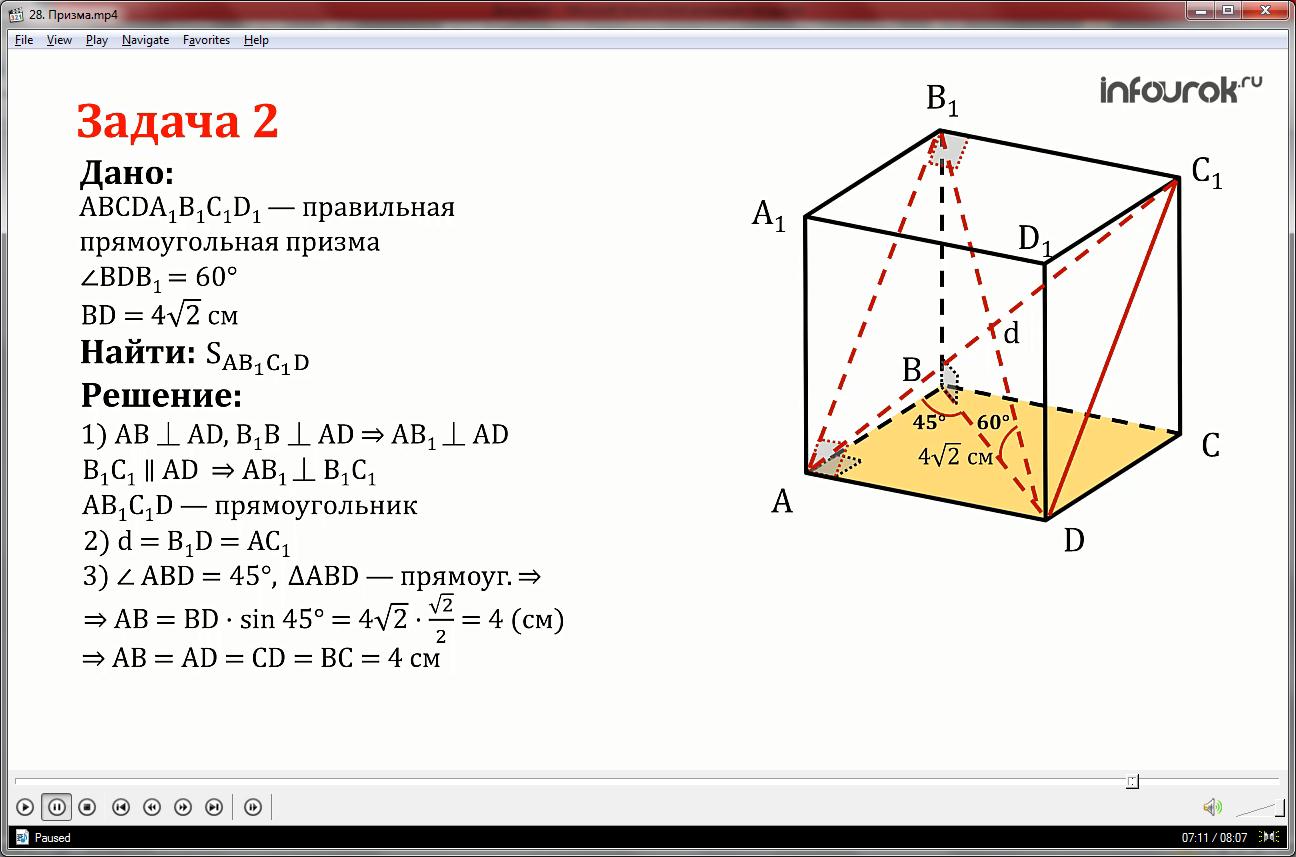
Из прямоугольного треугольника АВД по определению синуса(отношение противолежащего катета к гипотенузе) находим АВ как произведение ВД на синус 45 градусов.
АВ=ВД*sin 450=4√2* =4см, ABCD-квадрат, поэтому АВ=АД.
4.Из прямоугольного треугольника ВВ1Д находим ВВ1 с помощью определения тангенса(отношение противолежащего катета к прилежащему):
ВВ1 =tg 600*BD=√3*4√2=4√6 cм
5.Призма правильная, поэтому все её грани равны, соответственно диагонали граней так же равны между собой, поэтому ВД=ДС1. Из прямоугольного треугольника ДСС1 по теореме Пифагора найдем ДС1=√ДС2+ДС12=√42+(4√6)2=√16+16*6=√16(1+6)
=4√7см
6.Таким образом неизвестные отрезки АД и ДС1 известны, мы можем найти площадь сечения:
SAB1C1D=АД*ДС1=4*4√7=16√7 см
Ответ: SAB1C1D=16√7 см
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11199 |
| Номер материала | 942 |