
Урок «Признак перпендикулярности двух плоскостей»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.
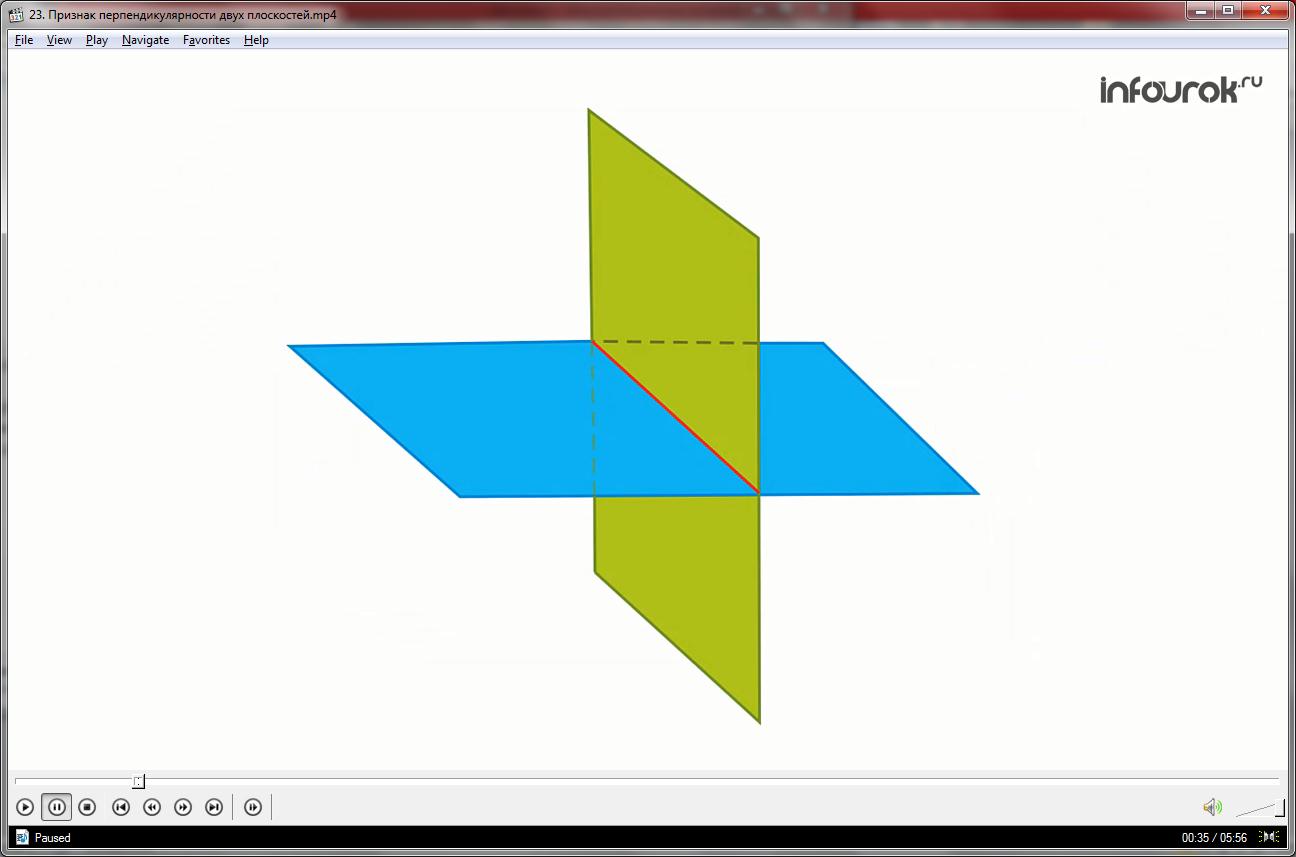
Рассмотрим две пересекающиеся плоскости. При пересечении они образуют четыре двугранных угла с общим ребром.
Вспомним, что из себя представляет двугранный угол.
В реальности мы встречаемся с предметами, которые имеют форму двугранного угла: например, приоткрытая дверь или полураскрытая папка.
При пересечении двух плоскостей альфа и бета получим четыре двугранных угла. Пусть один из двугранных углов равен (фи), тогда второй равен (1800 – ), третий , четвертый (1800- ).
Рассмотрим случай, когда один из двугранных углов равен 900.
Тогда, все двугранные углы в этом случае равны по 900.
Введем определение перпендикулярных плоскостей:
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
Угол между плоскостями сигма и эпсилон равен 90 градусов, значит плоскости перпендикулярны
Приведем примеры перпендикулярных плоскостей.
Стена и потолок.
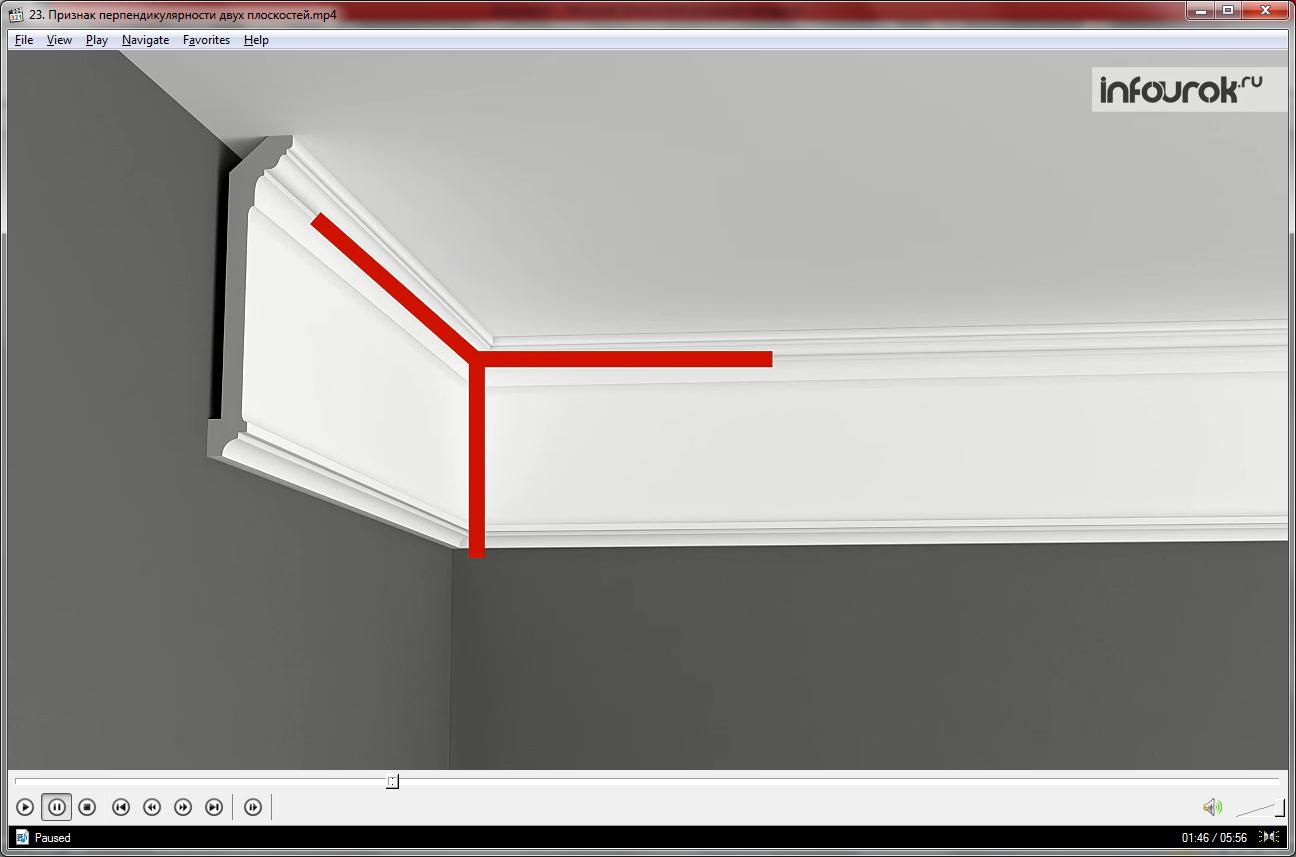
Боковая стенка и крышка стола.
Сформулируем признак перпендикулярности двух плоскостей:
ТЕОРЕМА: Если одна их двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Докажем этот признак.
По условию известно что прямая АМ лежит в плоскости α, прямая АМ перпендикулярна плоскости β,
Доказать: плоскости α и β перпендикулярны.
Доказательство:
1) Плоскости α и β пересекаются по прямой АР, при этом АМ АР, так как АМ β по условию, то есть АМ перпендикулярна к любой прямой, лежащей в плоскости β.
2) Проведем в плоскости β прямую AТ перпендикулярную AР.
Получим угол ТAМ – линейный угол двугранного угла. Но угол ТAМ = 90°, так как МА β. Значит, α β.
Что и требовалось доказать.
Из признака перпендикулярности двух плоскостей имеем важное следствие:
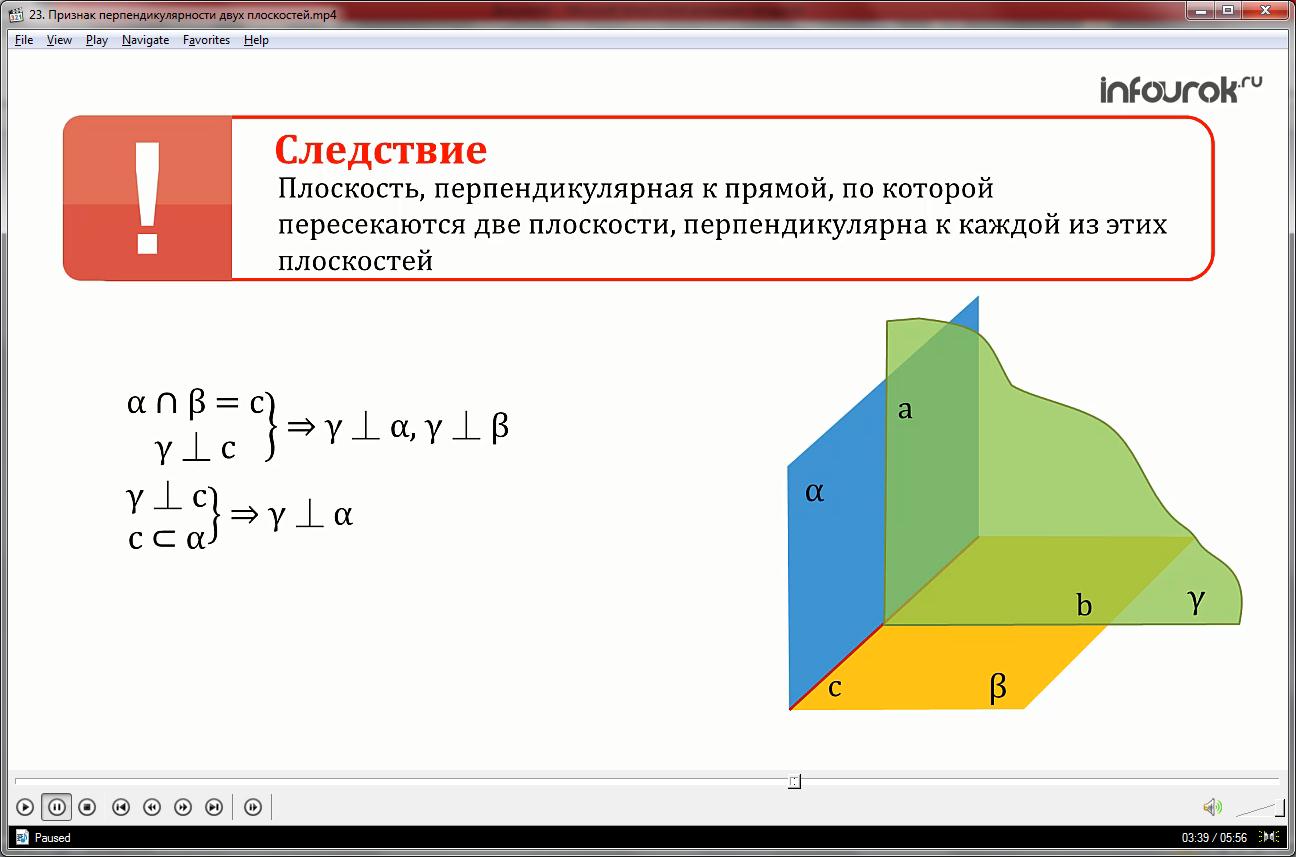
СЛЕДСТВИЕ: Плоскость, перпендикулярная к прямой, по которой пересекаются две плоскости, перпендикулярна к каждой из этих плоскостей.
То есть: если α∩β=с и γ с, то γ α и γ β.
Докажем это следствие: если плоскость гамма перпендикулрна к прямой с то по признаку параллельностидвух плоскостей гамма перпендикулярна к альфа. Аналогично и гамма перпендикулярна бета
Указанное следствие переформулируем для двугранного угла:
Плоскость, проходящая через линейный угол двугранного угла перпендикулярна ребру и граням этого двугранного угла. Другими словами, если мы построили линейный угол двугранного угла, то проходящая через него плоскость перпендикулярна ребру и граням этого двугранного угла.
Задача.
Дано: ΔАВС, С = 90°, АС лежит в плоскости α, угол между плоскостями α и ABC = 60°, АС = 5 см, АВ = 13 см.
Найти: расстояние от точки В до плоскости α.

Решение:
1) Построим ВК α. Тогда КС - проекция ВС на эту плоскость.
2) ВС АС (по условию), значит, по теореме о трех перпендикулярах (ТТП), КС АС. Следовательно, ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника АВС. То есть ВСК = 60°.
3) Из ΔВСА по теореме Пифагора:
Из ΔВКС:
Ответ ВК равно 6 корней из трех см
Практическое использование (прикладной характер) перпендикулярности двух плоскостей.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 17510 |
| Номер материала | 937 |