
Урок «Признак перпендикулярности прямой и плоскости»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Попробуем ответить на вопрос: Когда прямая перпендикулярна плоскости. Для этого рассмотрим модель параллелепипеда АВСDА1В1С1D1 в основании, которого лежит квадрат.
Например, попробуем найти прямую перпендикулярную плоскости АВСD. Рассмотрим прямую А1В.
Очевидно, что угол между прямой А1В и прямой АВ острый, а вот прямая ВС и прямая А1В перпендикулярны, как стороны диагонального сечения А1ВСD1 . Заметим, что прямые АВ и ВС пересекаются.
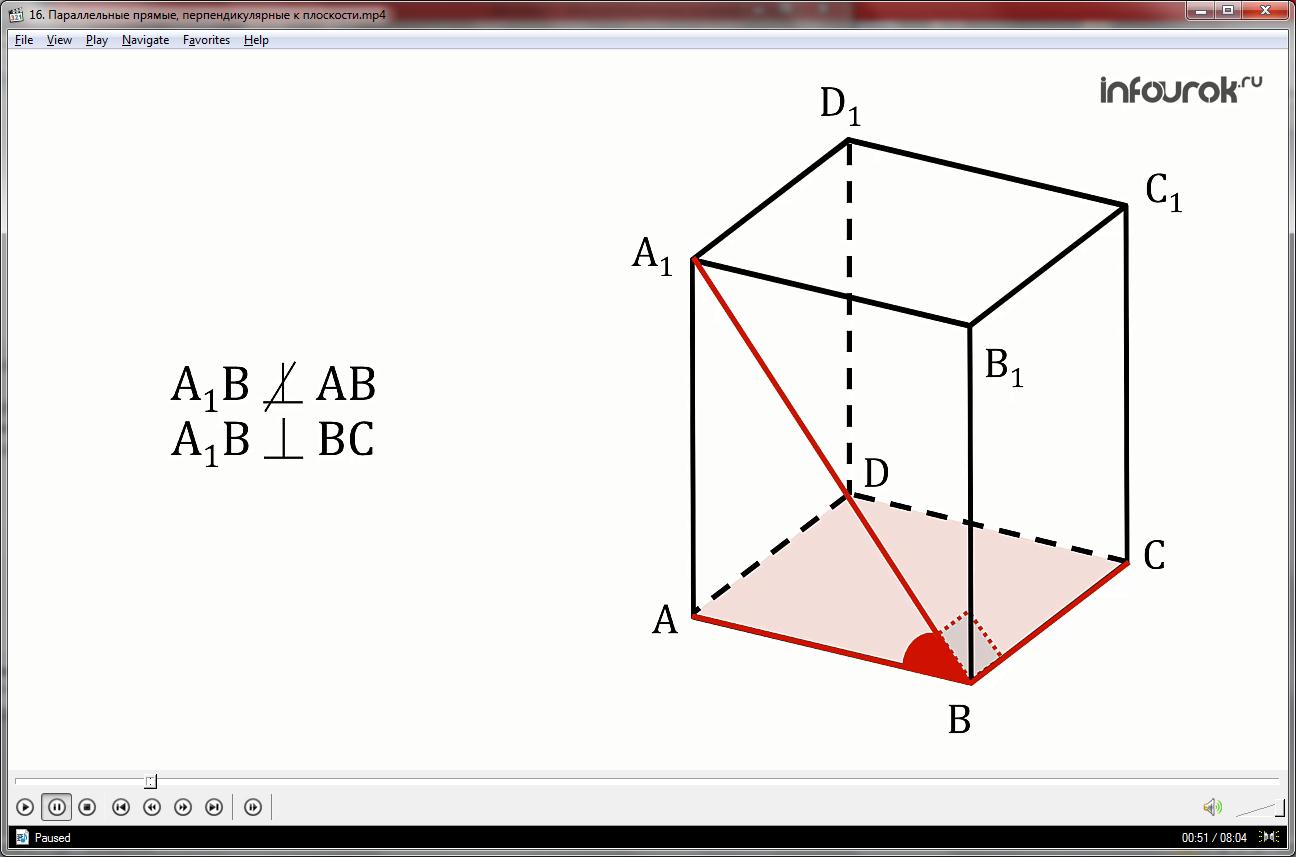
Рассмотрим прямую С1С . Прямая С1С перпендикулярна прямой ВС.
Одновременно прямая С1С перпендикулярна и прямой DС лежащей в плоскости А1ВСD1 . Заметим так же, что прямые DС и ВС пересекаются.
Рассмотрим еще один вариант расположения прямых. Пусть диагонали основания пересекаются в точке О, и по свойству квадрата отрезок DО равен отрезку ОB. Прямая С1О перпендикулярна прямой DВ по свойству равнобедренного треугольника DC1В. Но С1О не перпендикулярна прямой АС.
Какой же из вариантов определяет прямую перпендикулярную плоскости.
В геометрии прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Таким образом прямая А1В не удовлетворяет условию, она не перпендикулярна прямой АВ, лежащей в плоскости АВСD.
Аналогично и с рисунком в). Прямая ОС1 не перпендикулярна прямой АС, лежащей в плоскости АВСD.
А рисунок б) демонстрирует перпендикулярность прямой и плоскости.
На письме перпендикулярность прямой С1С и плоскости АВСD так.
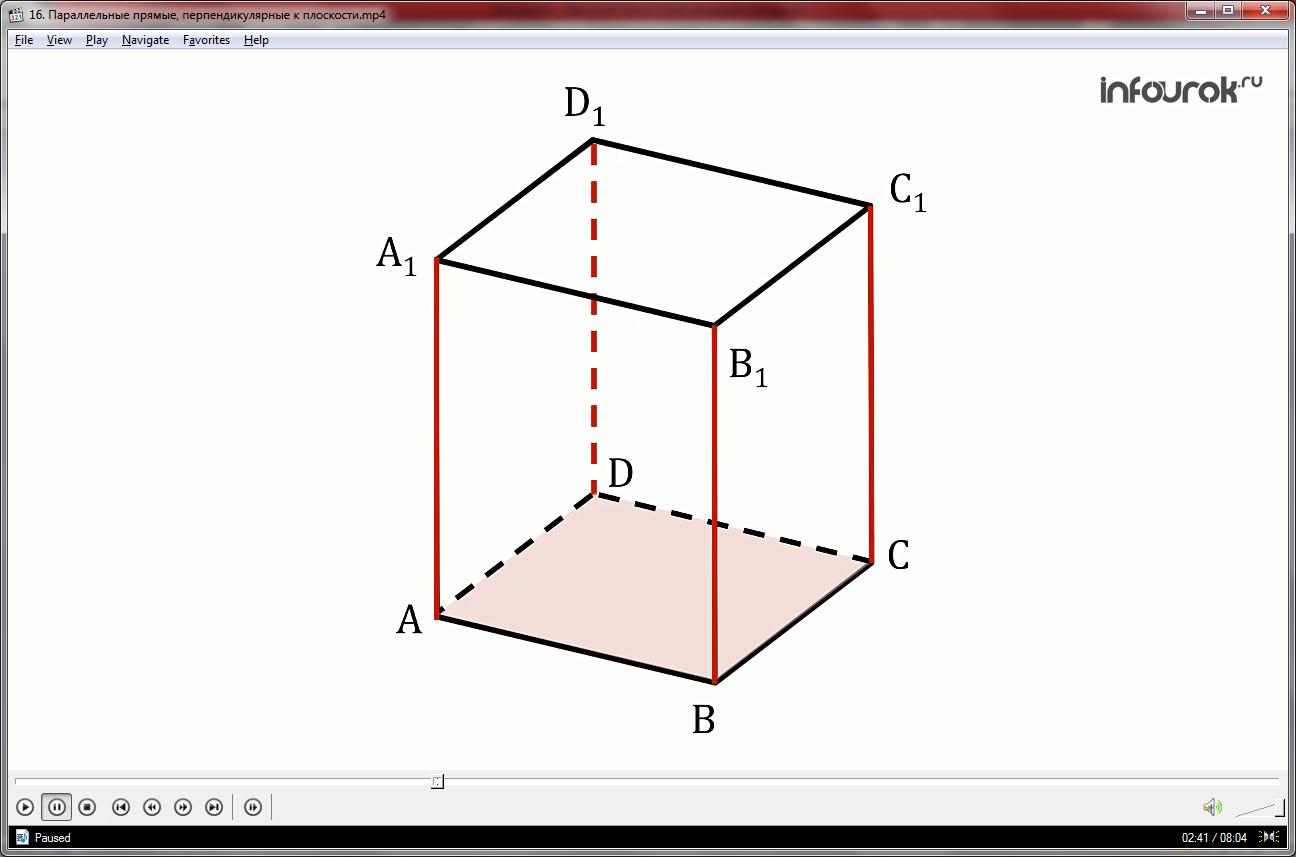
Помимо прямой С1С к плоскости АВСD в данном параллелепипеде перпендикулярны и рёбра А1А, D1D, В1В.
Это можно доказать аналогично ребру С1С. При этом они параллельны между собой.
Связь прямых и плоскости сформулирована в двух важных теоремах. Докажем их.
Теорема 1. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.
Для доказательства рассмотрим две параллельные прямые a и b , и плоскость α. Прямая а перпендикулярна плоскости α по условию.
Докажем, что прямая b перпендикулярна плоскости α.
1)Для доказательства проведём в плоскости α произвольную прямую с.
2)Так как прямая а у нас перпендикулярна плоскости α, то по определению она перпендикулярна произвольной прямой с лежащей в этой плоскости.
3)По теореме, доказанной на предыдущем уроке, если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна к этой прямой, т.е. прямые b и с перпендикулярны.
4)Аналогично можно доказать, что прямая b будет перпендикулярна любой другой прямой, лежащей в плоскости α.
Что доказывает перпендикулярность прямой b к любой прямой плоскости , тогда по определению прямой перпендикулярной плоскости, прямая b перпендикулярна плоскости α.
Для данного утверждения справедлива и обратная формулировка.
Достаточно интересно посмотреть применение данных теорем для решения задач.
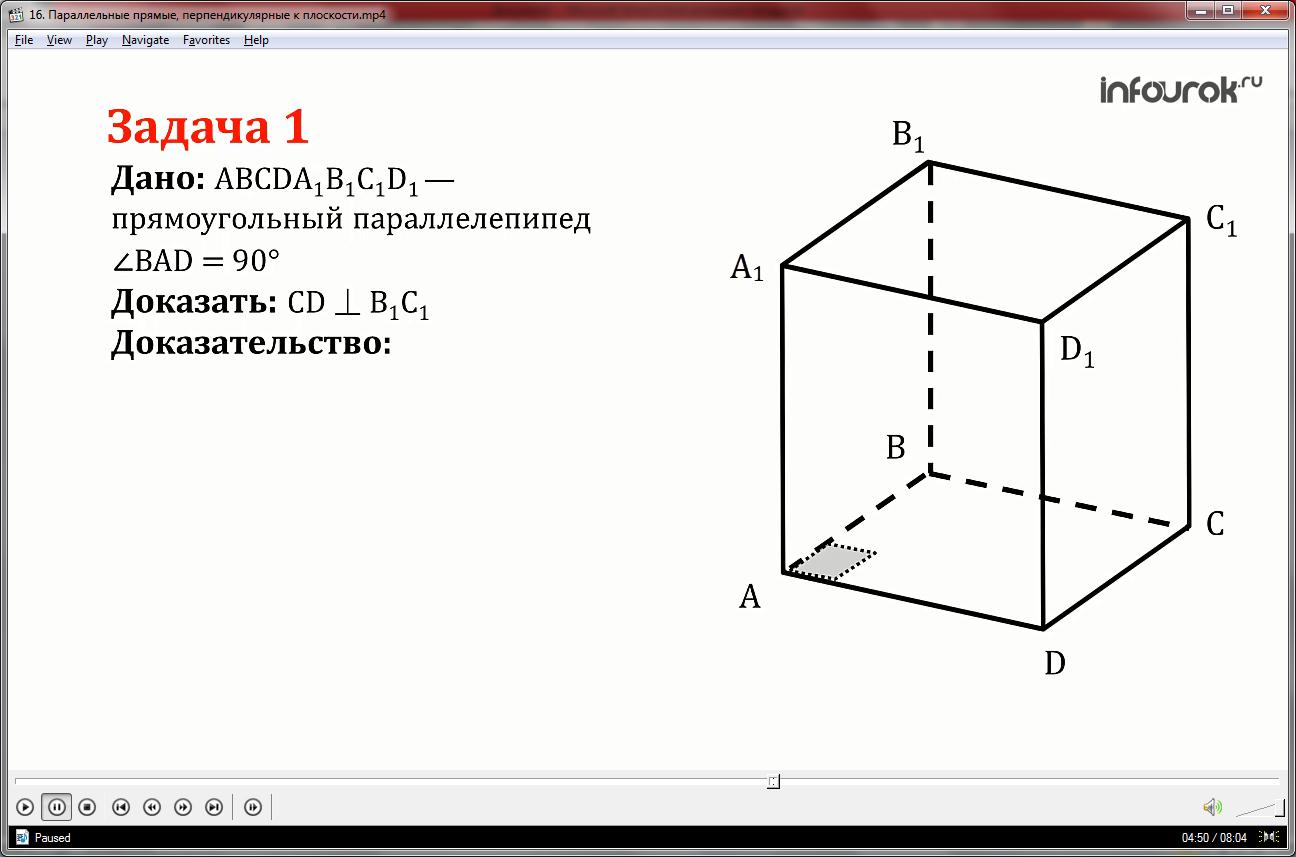
Дан параллелепипед АВСDА1В1С1D1 c углом ВАD равным 90 градусов.
1)У нас угол ВАD равен 90 градусов, значит АВСD – прямоугольник.
2,3)Таким образом прямая DC перпендикулярна прямой ВС, и прямая DС перпендикулярна прямой СС1, так как боковые грани прямоугольного параллелепипеда прямоугольники.
4)Так как прямая DC перпендикулярна прямым ВС и С1С плоскости В1ВСС1 , то по определению прямая DС перпендикулярна самой плоскости В1ВСС1.
5)Прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости. В данном случае прямая DC перпендикулярная прямой В1С1.
Рассмотри ещё один пример применения терем к решению задач.
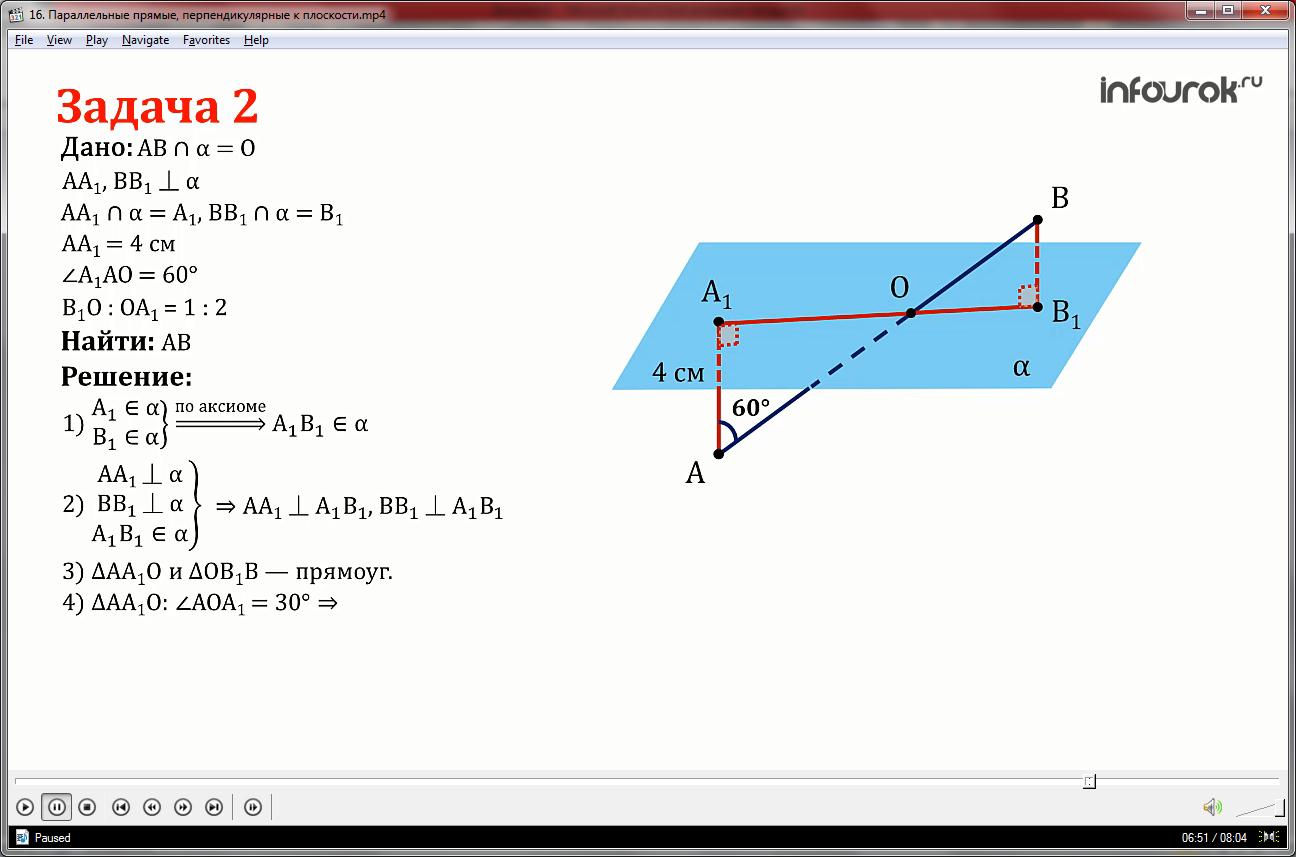
Нам дана плоскость α, отрезок АВ пересекает эту плоскость в точке О. Прямые АА1 и ВВ1 перпендикулярны к плоскости α, причём А1 и В1 лежат в плоскости. Известно, что АА1 4 см, а угол А1АО =60° и отрезок В1О относиться к отрезку А1О как 1 к 2.
1)Прямая А1В1 лежит в плоскости α, так как две точки прямой уже лежат в плоскости.
2)Прямые АА1 и ВВ1 перпендикулярны к плоскости α, тогда эти прямые перпендикулярна любой прямой лежащей в плоскости α, в частности прямой А1В1.
3)Тогда треугольники АА1О и ОВ1В прямоугольные.
4)В треугольнике угол АОА1 равен 30°, по свойству треугольника с таким углом катет АА1 равен половине гипотенузы, значит отрезок АО равен 8 см.
5)В треугольниках АА1О и ОВ1В угол АА1О равен углу ОВ1В, угол А1ОА равен углу ВОВ1 по свойству вертикальных углов, а стороны В1О и ОА1пропорциональны числам 1 и 2, значит треугольник АА1О подобен треугольнику ОВ1В по стороне и двум прилежащим к ней углам с коэффициентом подобия одна вторая.
6,7)Так как треугольники подобны, то ОВ относиться к стороне АО как 1 к 2. Получим, что сторона ОВ равна половине стороны АО и равна 4 см. А весь отрезок АВ состоящий из частей АО и ОВ равен 12 см.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7720 |
| Номер материала | 930 |