
Урок «Признак перпендикулярности прямой и плоскости»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
На разработку конструкции прибора инженер тратить достаточно много времени. Изменяя и модифицируя конструкцию прибора. Почему, например, бытовой вентилятор имеет именно такую форму ? Конструкция должна быть , такой что бы вентилятор не падал и прочно стоял перпендикулярно полу при работе. Конструкцию этого бытового прибора можно перенести на чертёж.
Пол мы заменим на плоскость α, штангу вентилятора изобразим в виде прямой а, ножки крепления в виде прямых b и с.
Предположим, что если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Докажем предположение.
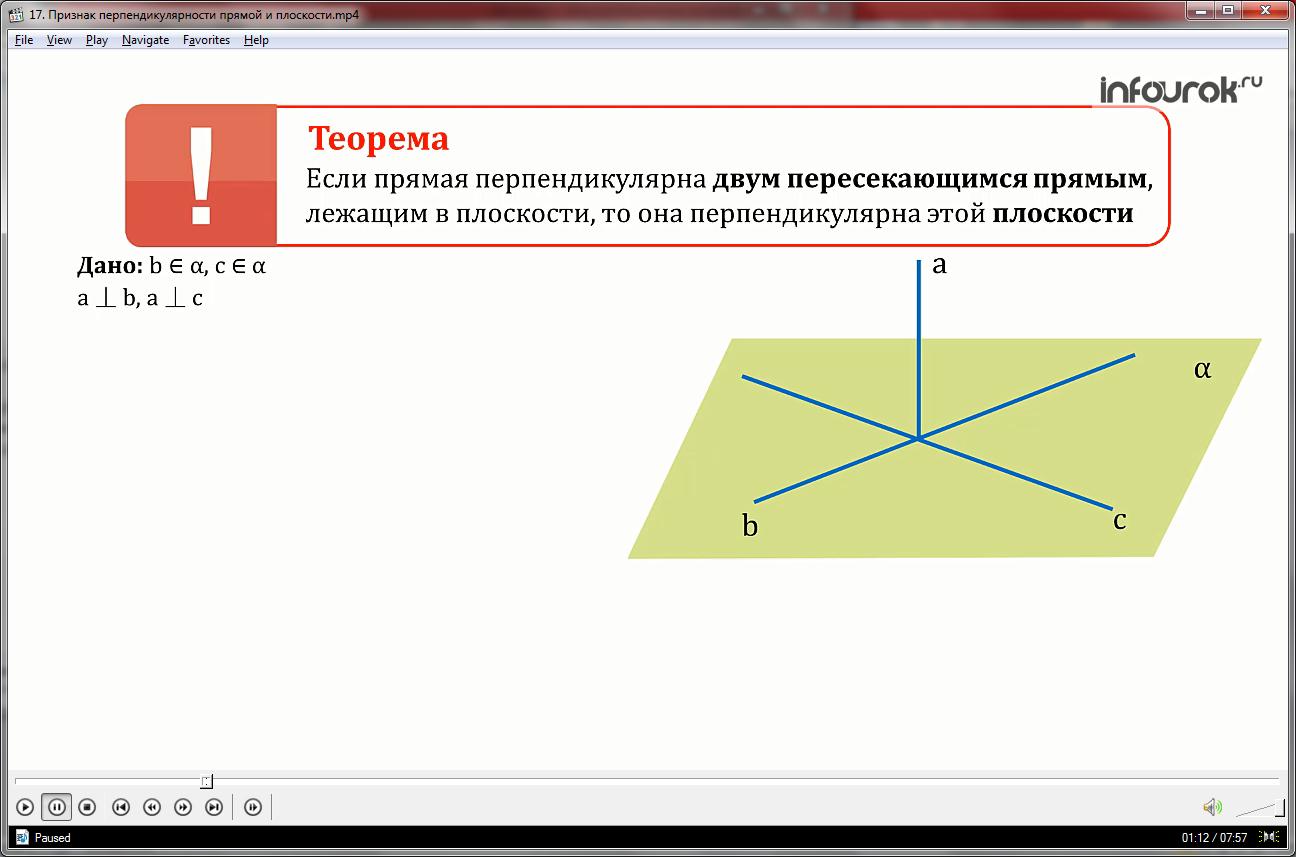
Рассмотрим нашу прямую а, которая будет перпендикулярна пересекающимся прямым b и с, лежащим в плоскости α. Обозначим точку пересечения прямых-точкой М.
Докажем, что прямая а перпендикулярна плоскости α.
Так как мы знаем, что прямая перпендикулярна плоскости, если перпендикулярна любой прямой лежащей в этой плоскости, то нам нужно доказать перпендикулярность прямой а произвольной прямой х.
Для доказательства построим дополнительно прямую у, параллельную прямой х и проходящую через точку М.
Дополнительно на прямой а отметим точки М1 и М2 так, чтобы точка М была серединой отрезка М1М2.
Так же проведём прямую в плоскости , пересекающую прямые b, с, у в точках В,С,Y соответственно.
Соединим полученные точки с концами отрезка М1М2. Так как прямые b и с перпендикулярны к прямой а и проходят через середину отрезка М1М2, то их можно назвать серединными перпендикулярами к отрезку М1М2. Тогда точки В и С равноудалены от концов отрезка, то есть отрезок М1В равен отрезку ВМ2, а отрезок М1С равен отрезку СМ2.

Треугольник ВМ1М равен треугольнику ВМ2М по трём сторонам. Из равенства треугольников следует, что угол М1ВY равен углу.
Тогда треугольники М1ВY равен треугольнику М2ВY по двум сторонам и углу между ними. Из равенства этих треугольников следует равенство отрезков М1Y и M2Y.
Это означает что треугольник М1YМ2 равнобедренный с основанием М1М2 и отрезок YМ его медиана, а по свойству медианы равнобедренного треугольника, проведенной к основанию треугольника, отрезок YМ является высотой, значит прямые у и а, содержащие эти отрезки, можно считать перпендикулярными.
Прямая у перпендикулярна прямой а, и параллельна прямой х. По лемме о перпендикулярности двух параллельных прямых к третьей прямой следует, что прямая х также перпендикулярна прямой а.
Итак, прямая а перпендикулярна любой прямой х, значит перпендикулярна плоскости α.
Но в этой теореме возможен ещё один случай расположения прямой а, который не демонстрирует наша конфигурация чертежа. Когда прямая а не проходит через точку пересечения прямых b и с.
Докажем и этот вариант.
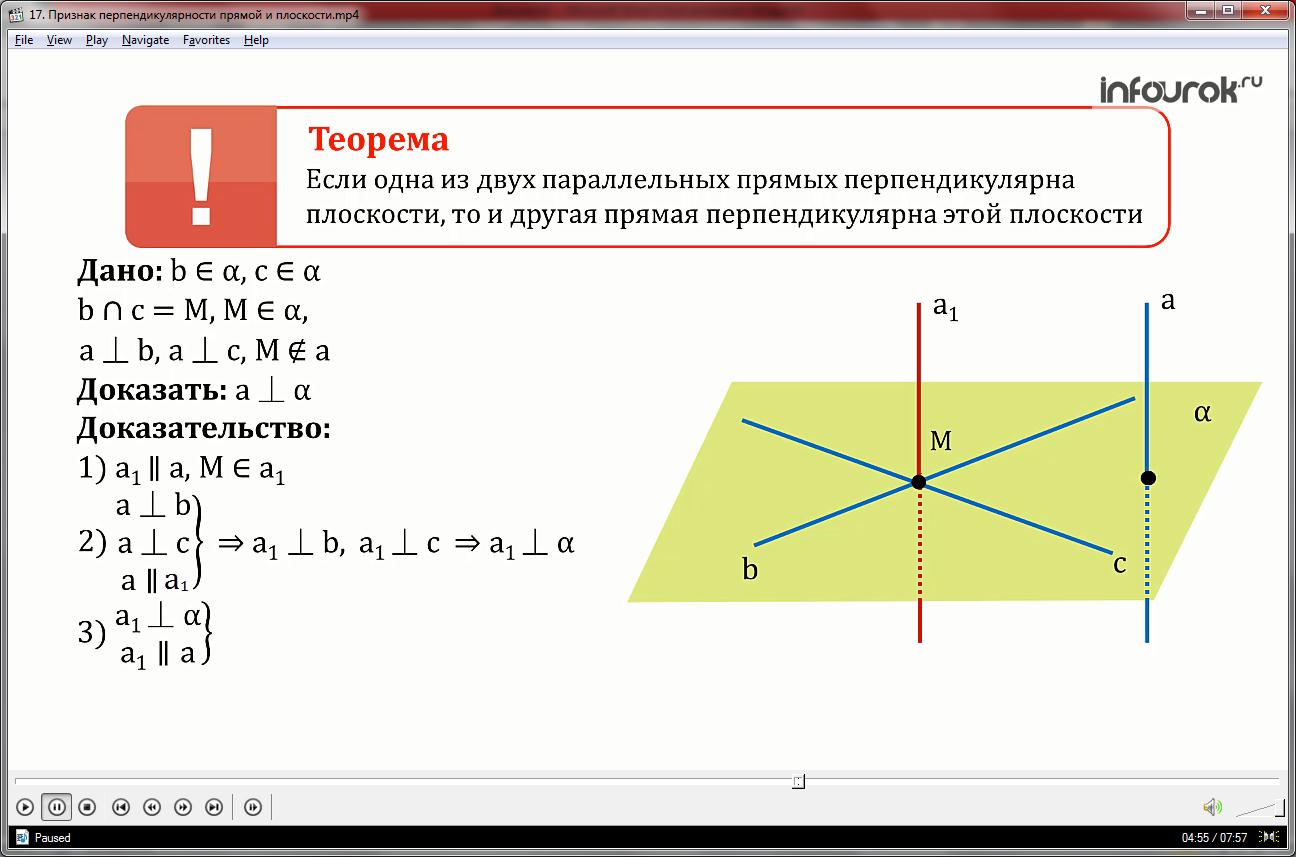
В этом случае проведём прямую а1, параллельную прямой а и проходящую через точку М.
Важно вспомнить теорему изученную на предыдущем уроке:
если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна этой плоскости.
Так как прямая а перпендикулярна прямым b и с и параллельна прямой а1, то по лемме прямая а1 тоже будет перпендикулярна прямым b и с.
В этом расположении прямых мы уже доказали перпендикулярность прямой к плоскости.
Но тогда если прямая а1 перпендикулярна плоскости и параллельна прямой а, то по теореме 1 прямая а перпендикулярна плоскости α.
Эта теорема даёт возможность доказать перпендикулярность прямой плоскости с указанием перпендикулярности только двум пересекающимся прямым, лежащим в этой плоскости, а не любой прямой. В геометрии данное утверждение называется признаком перпендикулярности прямой и плоскости.
Рассмотрим применение признака перпендикулярности прямой и плоскости.
Дан треугольник АВС с суммой углов А и В в 90 градусов. Прямая ВD проведена перпендикулярно к плоскости треугольника АВС.
Прямая СD лежит в плоскости треугольника ВСD.
Треугольник АВС прямоугольный, так как угол АСВ равен разности 180 градусов и суммы углов А и В. Значит прямая АС перпендикулярна прямой ВС.
По условию прямая BD перпендикулярна плоскости АВС, значит она перпендикулярна прямой АС.
Тогда прямая АС перпендикулярна двум пересекающимся прямым ВС и ВD лежащим в плоскости треугольника ВСD, значит АС перпендикулярна к плоскости ВСD и перпендикулярна прямой СD лежащей в этой плоскости.
Рассмотри ещё пример решения задачи.
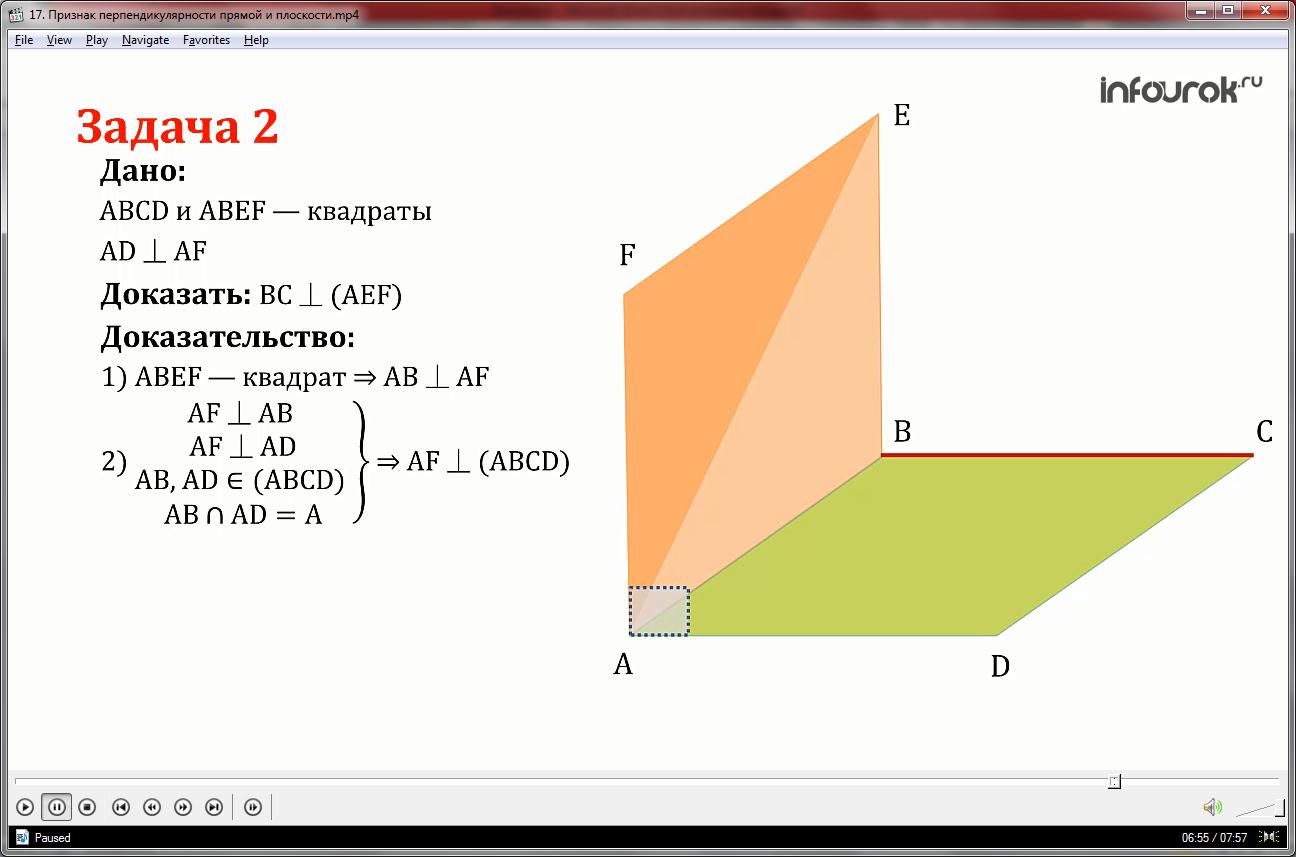
Даны два квадрата АВСD и АВEF.Они расположены так, что бы сторона AD AF.
Так как АВEF- квадрат, то прямая AВ перпендикулярна стороне AF.
Тогда по признаку перпендикулярности прямой и плоскости АF плоскости квадрата АВСD и прямой ВС лежащей в этой плоскости.
По определению квадрата АВСD сторона ВС перпендикулярна прямой АВ, но прямая АВ параллельна прямой FЕ плоскости АВEF, следовательно по лемме о параллельных прямых перпендикулярных к третьей прямой, прямая FE перпендикулярна прямой ВС.
Таким образом, прямая ВС перпендикулярна пересекающимся прямым АF и FE лежащим в плоскости AEF, что следовательно по признаку перпендикулярности прямой к плоскости, значит прямая ВС перпендикулярна к плоскости AEF.
В дальнейшем с помощью данного признака будут доказаны несколько главных теорем о перпендикулярности прямых и плоскостей в просранстве.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 22477 |
| Номер материала | 931 |