
Урок «Прямоугольный параллелепипед»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Для изучения сегодняшней темы поговорим о незаменимом помощнике каждого школьника –ластике.
Что можно сказать о форме ластиков?
Что бы анализировать форму предметов было удобно, перенесем их на чертёж.
Итак, первый ластик изобразим в форме фигуры в основании которой лежит прямоугольник, такой же прямоугольник и в верхней параллельной плоскости. Боковые грани прямоугольники, причём противоположные грани, равные прямоугольники. Получилась вот такая фигура. И нам она знакома –это параллелепипед.
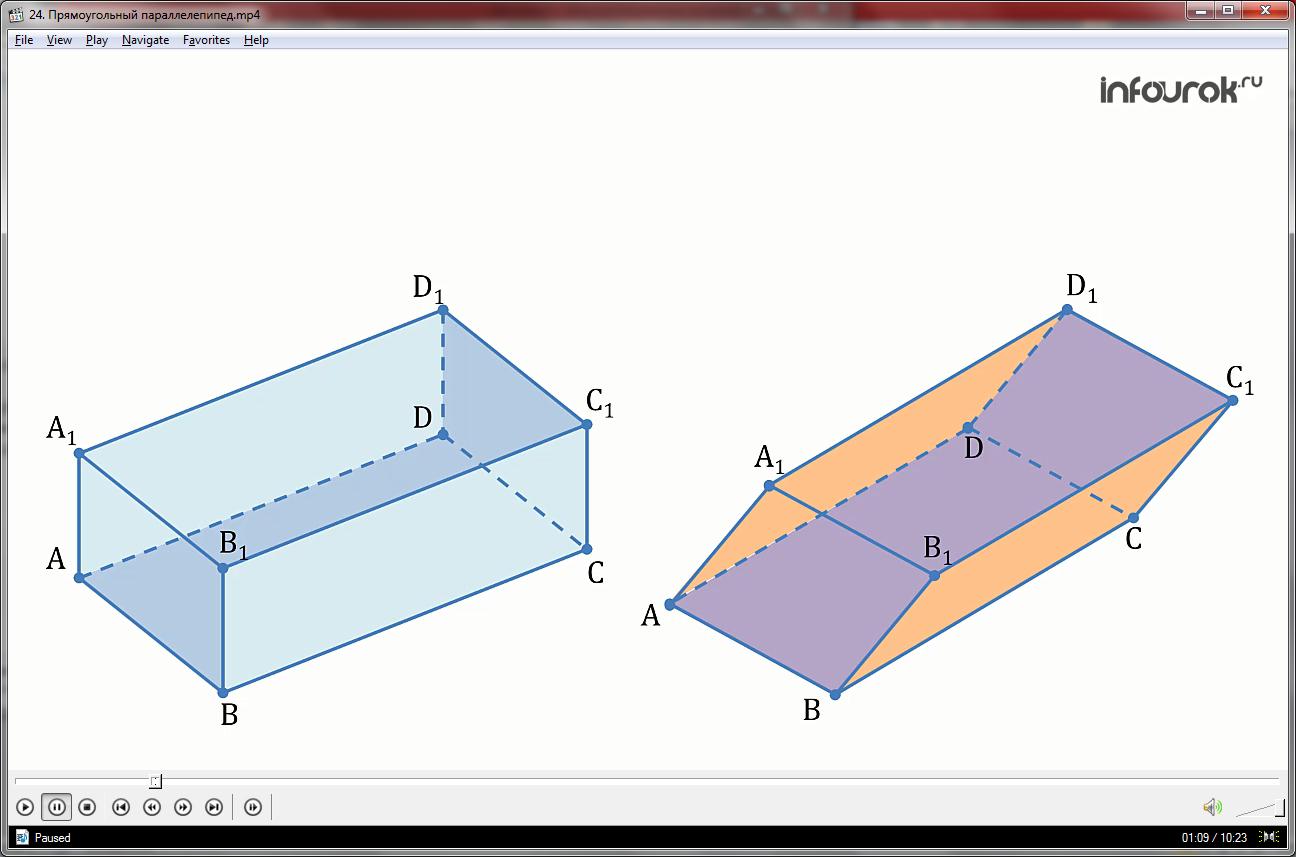
У второго ластика лишь одно отличие. Две боковых грани ластика параллелограммы. И это тоже параллелепипед. В чём же тогда фокус?
Дело в том, что оба ластика действительно демонстрируют геометрическую фигуру параллелепипед, но разные его виды. Давайте разберемся в подробностях.
Параллелепипед, ребра которого перпендикулярны к плоскости основания, называется прямым параллелепипедом. У такого параллелепипеда все грани прямоугольники.
Параллелепипед, ребра которого наклонены к плоскости основания, под острым углом, называется наклонным параллелепипедом.
А прямой параллелепипед в основании которого лежит прямоугольник, называется прямоугольным параллелепипедом.
На этом виде параллелепипеда мы и остановимся по подробней, так как это самая распространяя форма окружающих нас предметов.
Посмотрите сами.
Книги, блок от компьютера, микроволновая печь и многое другое.
Прямоугольный параллелепипед обладает рядом свойств.
Свойство 1. В прямоугольном параллелепипеде все шесть граней прямоугольники.
Для доказательства этого утверждения рассмотрим прямоугольный параллелепипед АВСВA1B1C1D1. Его основаниями служат прямоугольники АВСD, A1B1C1D1, а боковые ребра АА1, ВВ1, СС1, DD1 перпендикулярны основаниям, значит ребро ВВ1 перпендикулярно ребру ВС и АВ, ребро DD1 перпендикулярно ребру АD и DС, то есть боковые грани параллелепипеда являются прямоугольниками. Что и требовалось доказать.
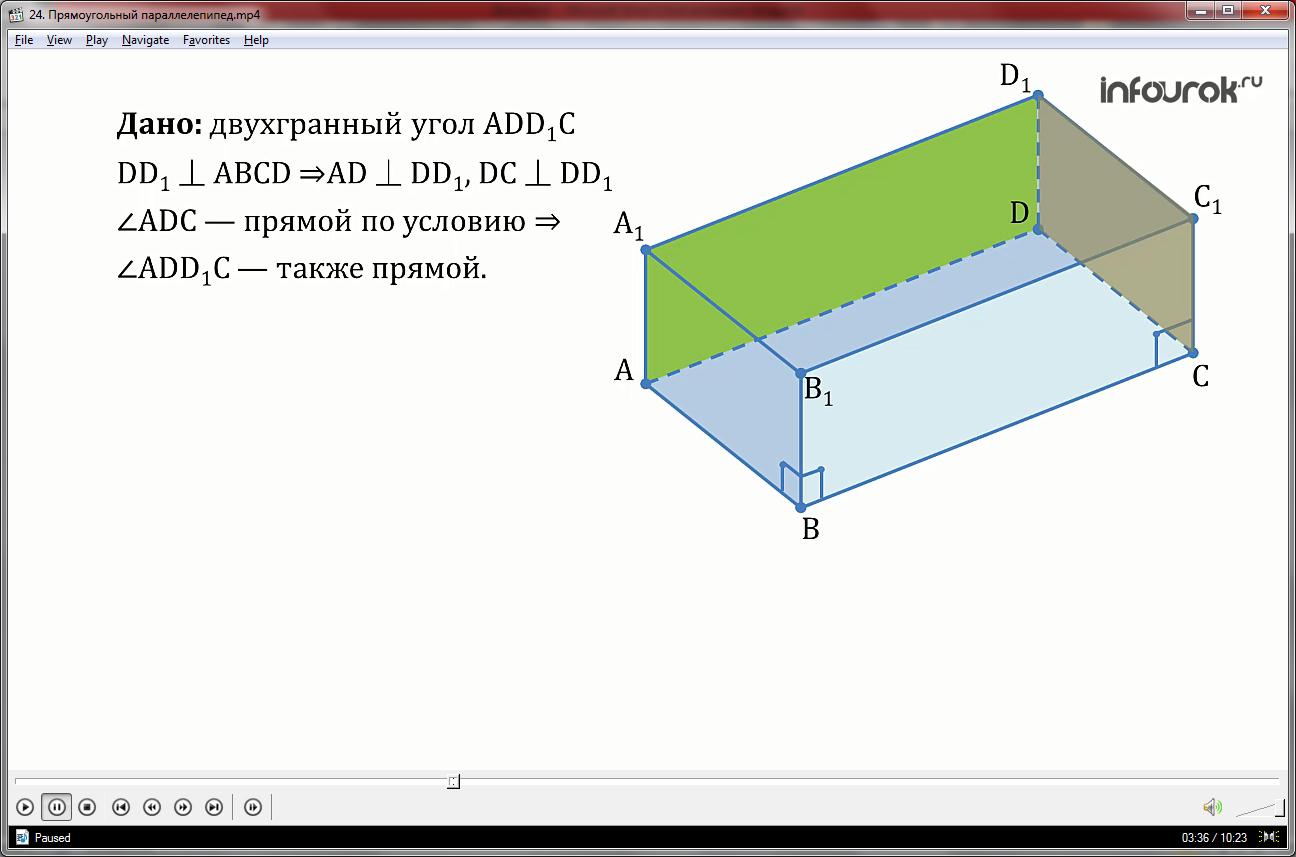
При этом грани параллелепипеда образуют двугранные углы. Рассмотрим двухгранный угол ADD1C. Так как ребро DD1 перпендикулярно плоскости основания по определению прямоугольного параллелепипеда, значит ребра AD и DC перпендикулярны ребру угла и образуют линейный угол данного двухгранного угла. Но угол ADC по условию, значит и двухгранный угол ADD1C также прямой. Аналогичное утверждение можно сформулировать для ещё одиннадцати двухгранных углов прямоугольного параллелепипеда. Значит, это свойство углов можно выделить как свойство номер 2. Итак свойство 2–все двухгранные углы прямоугольного параллелепипеда –прямые.
Для следующего свойства нужно вспомнить, что в пространстве прямоугольный параллелепипед характеризуется шириной, длиной и высотой. Длины этих трех ребер назовем измерениями прямоугольного параллелепипеда
В силу этих изменений, для основания длину и ширину можно назвать измерениями прямоугольника. И свойство диагонали прямоугольника сформулировать так: квадрат диагонали прямоугольника равен сумме квадратов двух его измерений.
Это утверждение было доказано ранее.
А мы докажем, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
То есть для параллелепипеда АВСВA1B1C1D1 докажем, что .
Мы уже сказали, что диагональ АС прямоугольника АВСD равна сумме квадратов ребер АВ и ВС, но диагонали прямоугольника равны, значит квадрат диагонали DB равен сумме квадратов ребер АВ и ВС.
Ребро ВВ1 по определению прямоугольного параллелепипеда перпендикулярно плоскости основания, значит перпендикулярно диагонали основания DB и треугольник прямоугольный. Значит, для треугольника справедлива теорема Пифагора. Квадрат диагонали равен сумме квадратов катетов DB и .
Подставим в равенство значение диагонали DB и получим выражение.
Что и требовалось доказать.
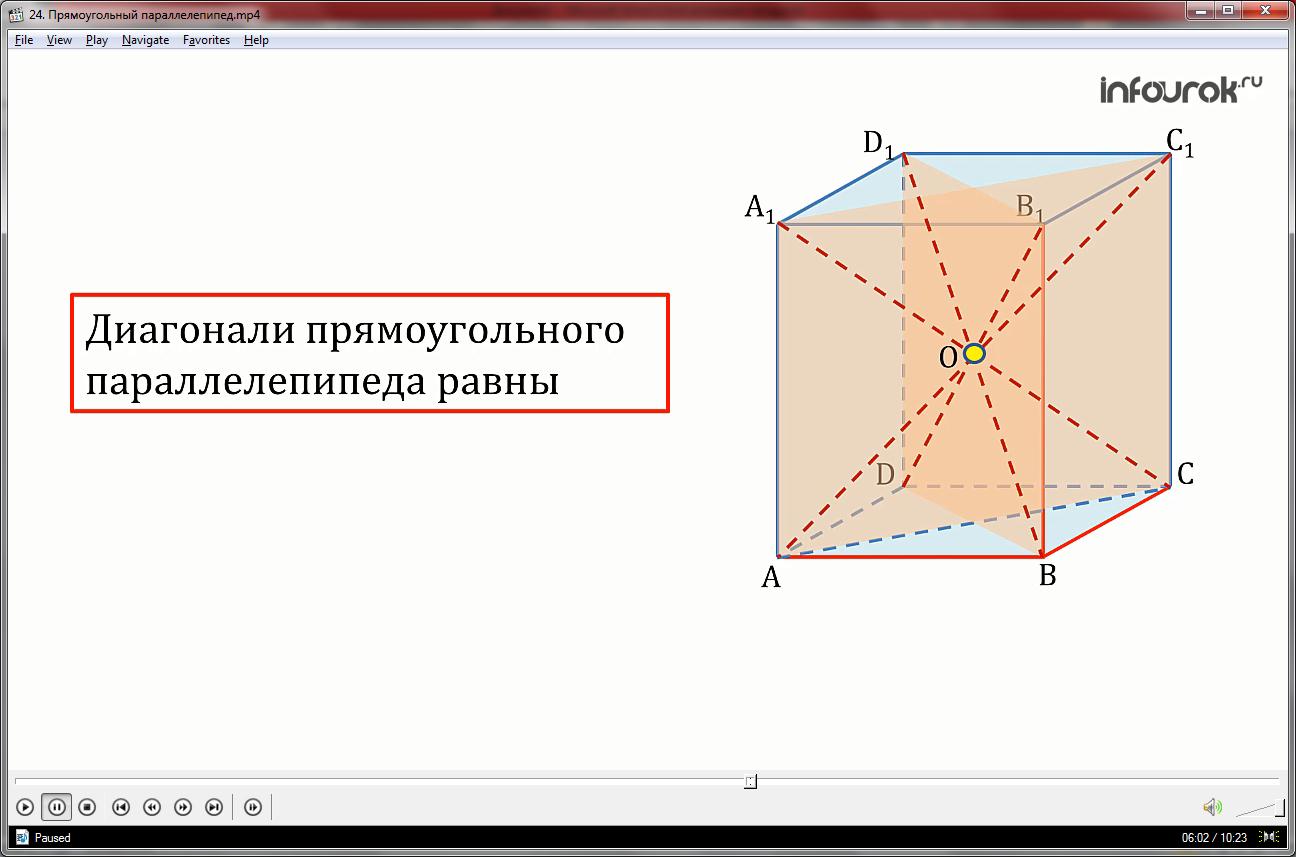
Прямоугольники DD1B1B и АА1С1С равны, так как равны их стороны. Значит диагонали этих прямоугольников также равны, но они являются диагоналями прямоугольного параллелепипеда, следовательно справедливо утверждение – диагонали прямоугольного параллелепипеда равны. Это утверждение можно считать следствием доказанного свойства.
Следует отметить, что прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Грани такого параллелепипеда равные квадраты.

Рассмотрим применение доказанных свойств при решении задач.
Задача первая. Диагонали граней прямоугольного параллелепипеда равны 11 см, 19 см и 20 см. Найдите диагональ параллелепипеда.
Построим указанный прямоугольный параллелепипед и обозначим его АВСВA1B1C1D1. Пусть диагональ ВС1 равна 11 см,
диагональ А1В равна 19 см,
диагональ DВ равна 20 см.
Для удобства обозначим три измерения прямоугольного параллелепипеда буквами а,b,c. А искомую диагональ буквой d. Тогда по свойству квадрат диагонали будет равен выражению.
По теореме Пифагора из прямоугольного треугольника А1АВ справедливо равенство
По теореме Пифагора из прямоугольного треугольника С1СВ справедливо равенство
По свойству прямоугольника АВСD справедливо равенство
Составим систему из полученных равенств. Почленно сложим эти равенства. Получили удвоенную сумму квадратов трех измерений параллелепипеда.
А это есть диагональ . После преобразований выражения получили, что диагональ равна 21 см.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 13516 |
| Номер материала | 938 |