
Урок «Расстояние от точки до плоскости»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Ранее было рассмотрено, что через точку А, не лежащую на плоскости α, можно провести только одну прямую, перпендикулярную к этой плоскости.
Дана плоскость α и точка А, не лежащая на ней.
Проведем из точки А прямую, перпендикулярную к плоскости α. Обозначим буквой Н точку пересечения проведенной прямой с плоскостью α.
Определение:
Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АН. Точка Н называется основанием этого перпендикуляра.
Возьмем произвольную точку М, принадлежащую плоскости α и отличную от Н. Соединим точки А и М.
Определение:

Отрезок АМ называется наклонной, проведенной из точки А к плоскости α. Точка М называется основанием наклонной.
Соединим точки М и Н.
Определение:
Отрезок МН называется проекцией наклонной АМ на плоскость α.
Имеется точка А и два отрезка, проведенных из этой точки к плоскости α: отрезок АН и отрезок АМ. Как вы думаете, какой из этих отрезков меньше?
Рассмотрим отрезки АН и АМ.
Для этого рассмотрим треугольник АНМ. Это прямоугольный треугольник, так как угол АНМ равен 90 градусам (так как АН перпендикулярна плоскости α). Тогда сторону АН можно назвать катетом, а сторону АМ гипотенузой. Но гипотенуза всегда больше катета. Поэтому АН < АМ.
Значит, перпендикуляр, проведенный из точки, не лежащей на плоскости, к этой же плоскости, всегда меньше любой наклонной, проведенной из той же точки к этой же плоскости.
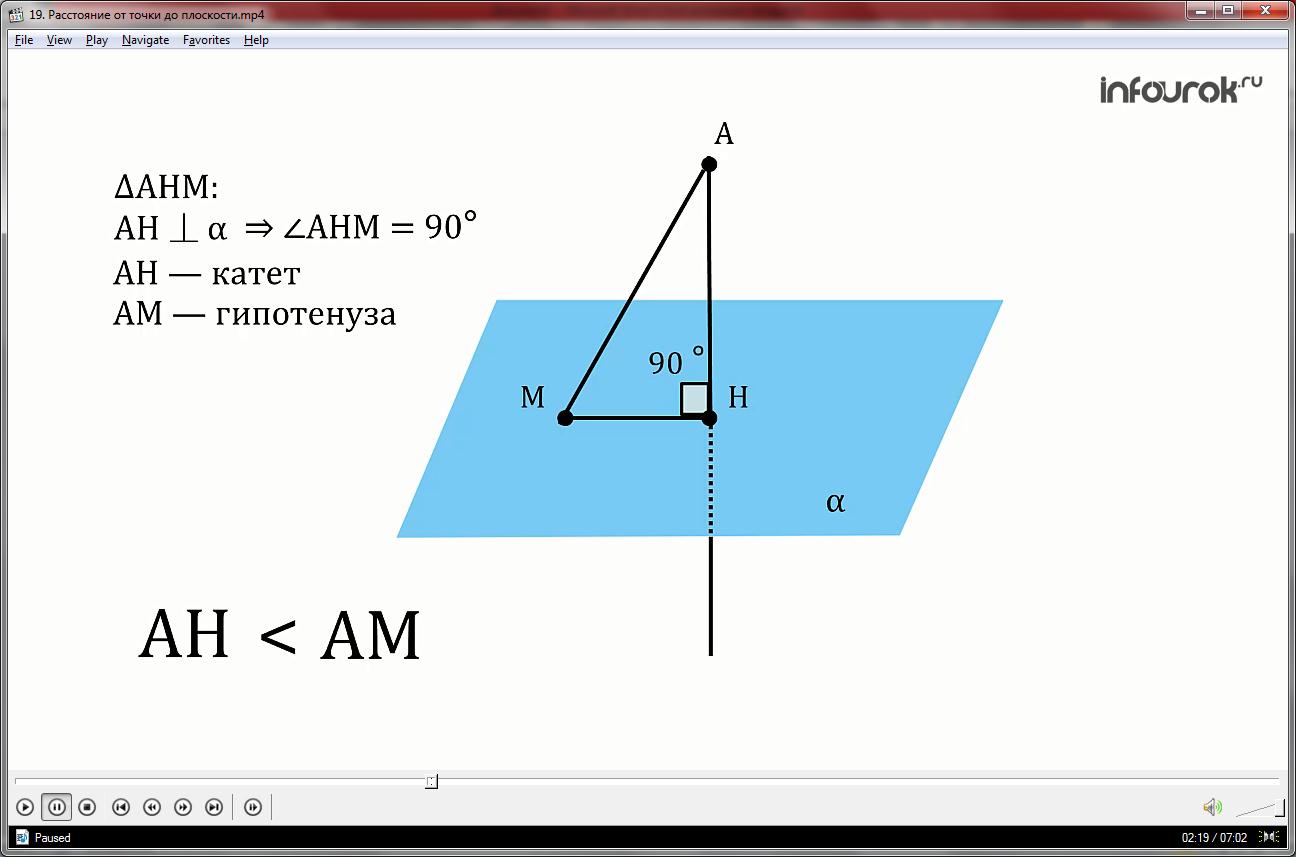
Таким образом из всех расстояний от точки А до разных точек плоскости α наименьшим является расстояние до точки Н.
Определение:
Расстоянием от точки А до плоскости α называется длина перпендикуляра АН, проведенного к плоскости α.
Рассмотрим решение типовой задачи по теме.
Задача.
Из точки А, не принадлежащей плоскости α, проведены перпендикуляр АО и две равные наклонные АМ и АН. Известно, что АО = 3 единицам, АМ = АН = 5 единицам. Найти расстояние между основаниями наклонных.
Решение:
Из прямоугольного треугольника АОМ найдем ОМ по теореме Пифагора. ОМ² = 25 – 9 = 16 или ОМ=4 единицы. Тогда МН=2*ОМ = 8 ед.
Ответ: МН=8 ед.
Рассмотрим три замечания к теме, которые необходимы для решения задач.
Замечание 1
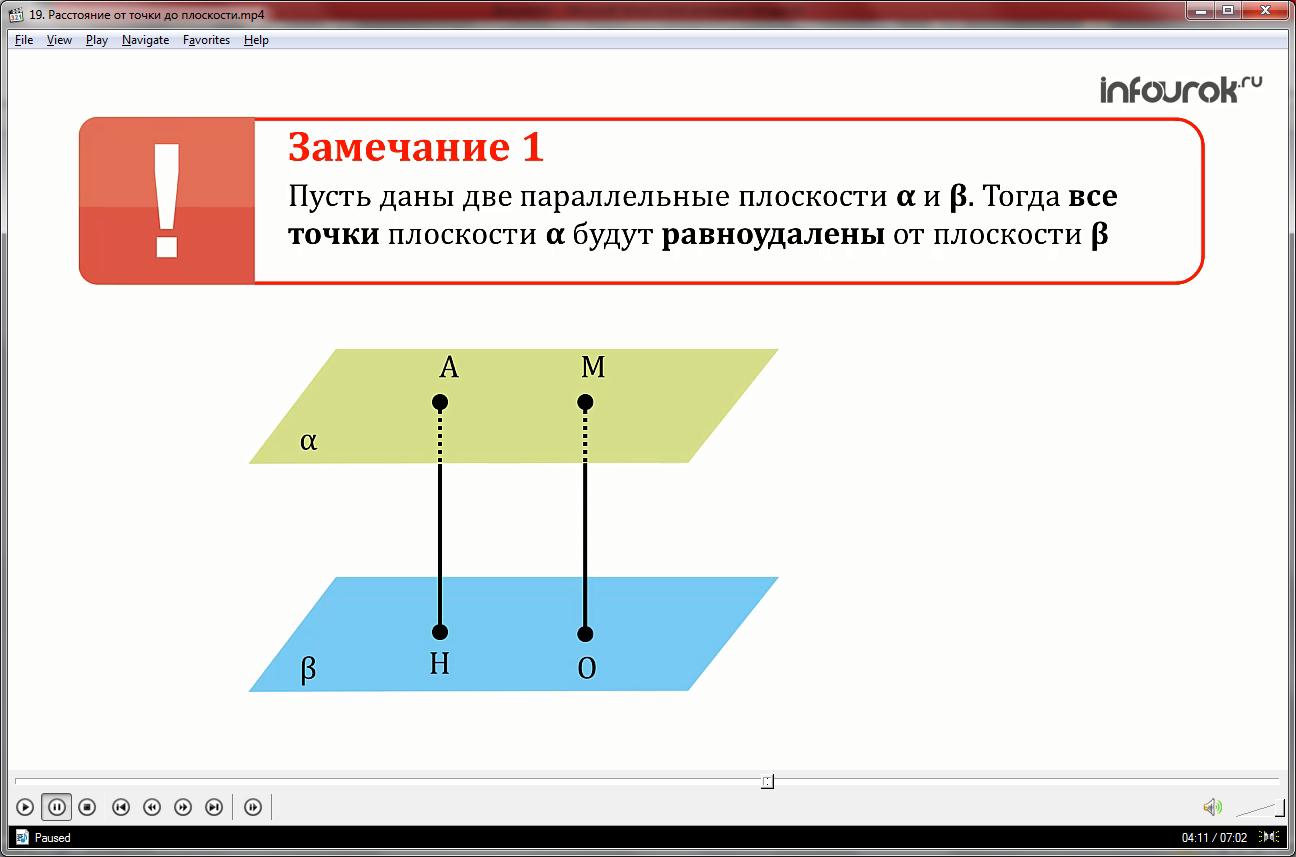
Пусть даны две параллельные плоскости α и β. Тогда все точки плоскости α будут равноудалены от плоскости β.
Действительно. На плоскости α взяты произвольные точки А и М. Из этих точек на плоскость β опустим перпендикуляры АН и МО соответственно. Следовательно, перпендикуляр АН параллелен перпендикуляру МО.
Эти перпендикуляры будут равными, по второму свойству параллельности плоскостей, которое звучит так: отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Определение.
Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой.
На рис расстоянием между параллельными плоскостями α и β является отрезок, например, МО.
Замечание 2
Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости.
Выберем любую точку А на прямой а, опустим перпендикуляр АО на плоскость α.
Определение.
Длина перпендикуляра АО называется расстоянием между прямой а и параллельной ей плоскостью α.
Задача.
Найдите расстояние между прямой МН и плоскостью параллельного ей прямоугольника АВСД, если известно, что МН=6см; угол МНО=45 градусам (см. рис 015).
Дано: МН || АВСД; МН=6см; МНО=45°; МО АВСД
Найти: МО
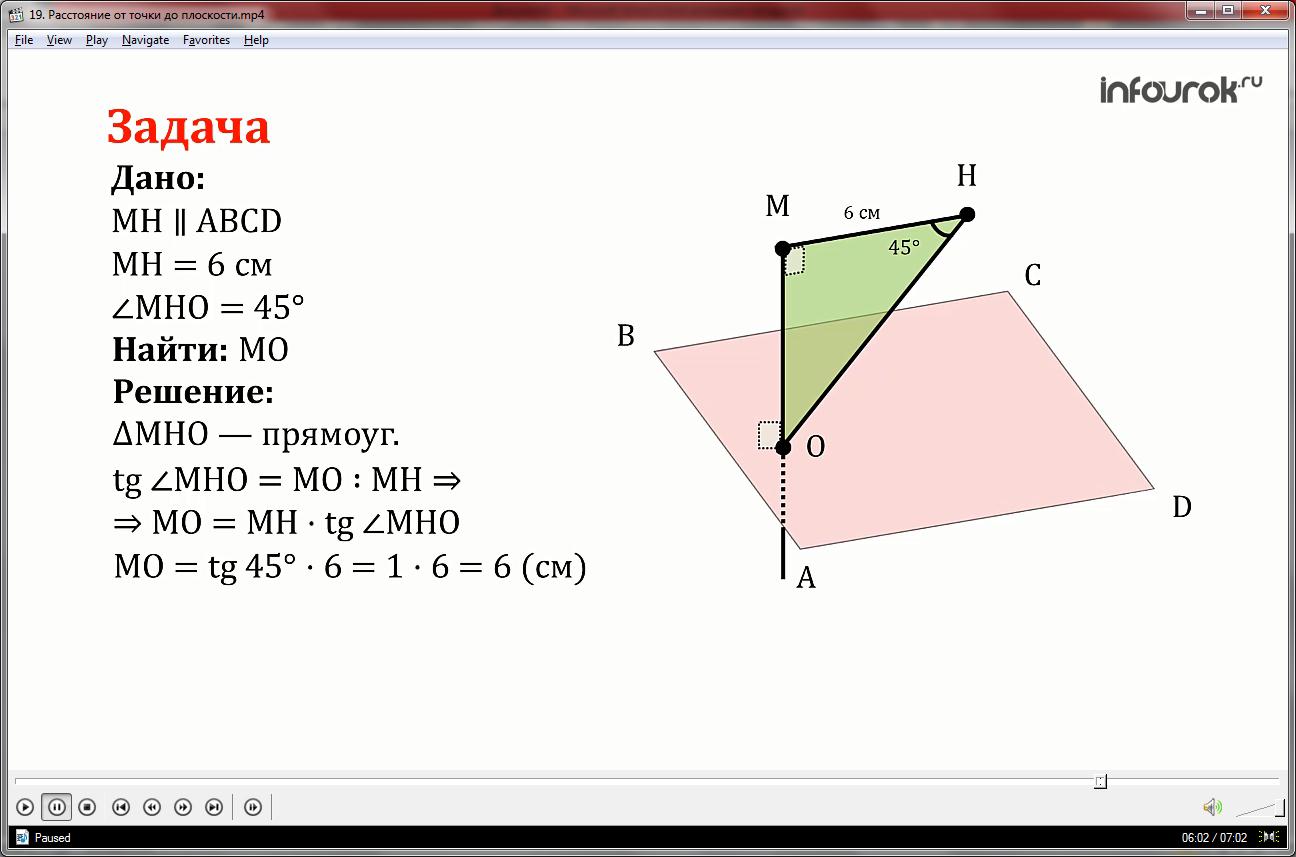
Решение:
МНО прямоугольный. Используя определения тригонометрической функции тангенс (Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету), имеем МО=tg45°*6=1*6=6см
Ответ: 6см
Замечание 3
Пусть прямые а и b скрещивающиеся. Тогда плоскость α, проходящая через прямую а, параллельна прямой b (по теореме: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой и притом только одна.).
Определение.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
На рис расстоянием между скрещивающимися прямыми а и b является отрезок МО.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11561 |
| Номер материала | 933 |