
Урок «Равенство векторов»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем определение равных векторов.
Векторы называются равными, если они сонаправлены и их длины равны.
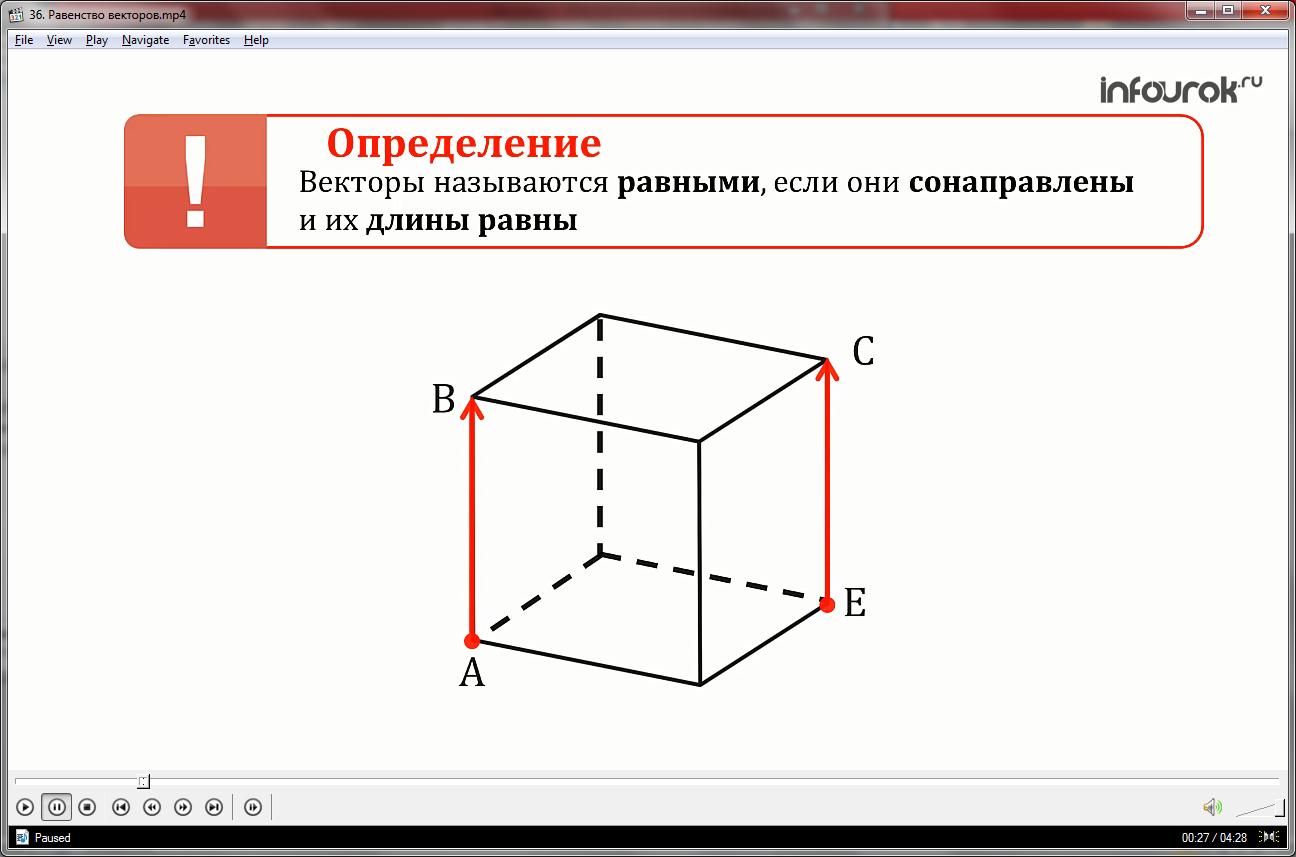
Для примера рассмотрим прямоугольный параллелепипед. Векторы АВ и ЕС, отмеченные на параллелепипеде, равны, так как они сонаправлены и их длины равны.
А на этом рисунке векторы АВ и СМ неравны, так как они сонаправлены, но их длины неравны.
На этом параллелепипеде векторы АН и ОК так же неравны, так как нарушено условие сонаправленности.
Если точка М – начало вектора а, то говорят, что вектор а отложен от точки М.
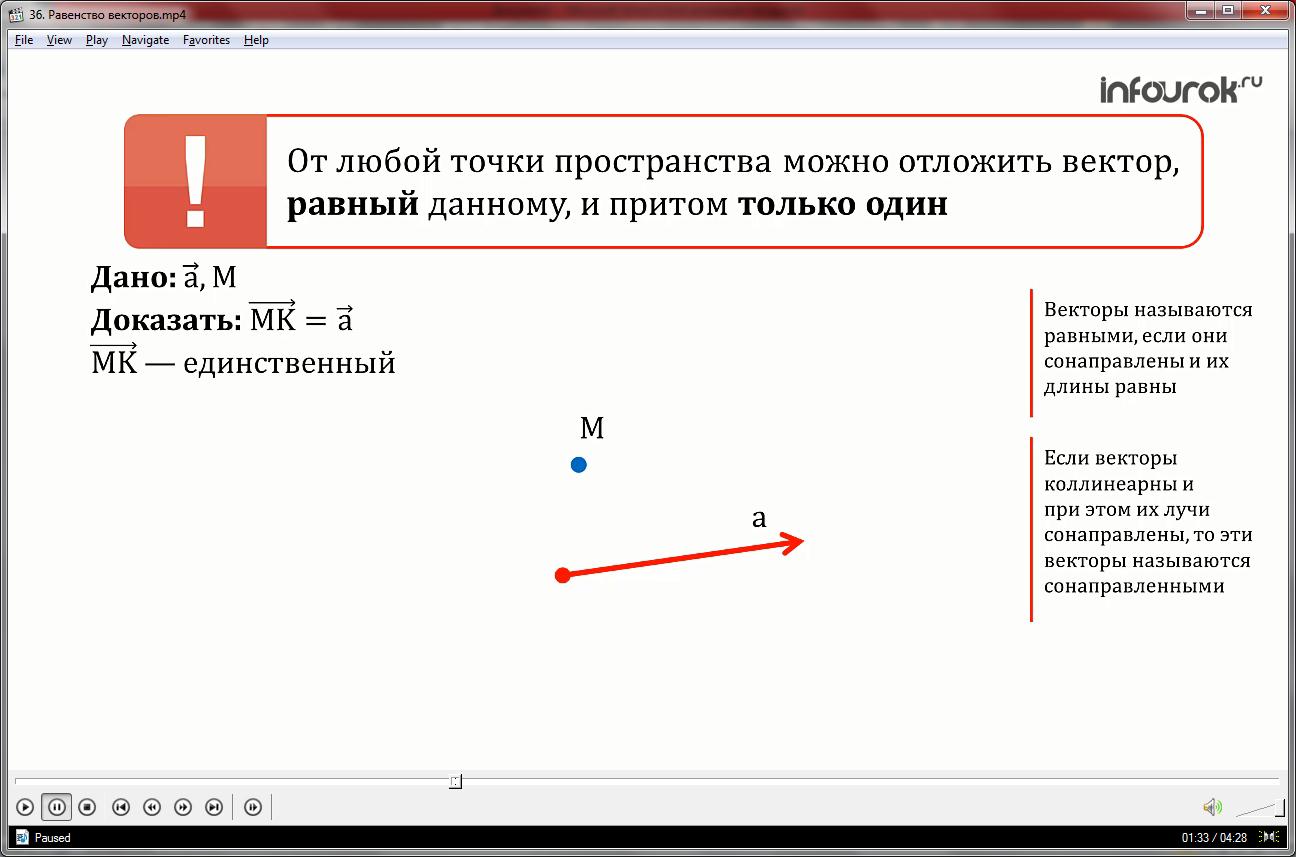
Докажем, что от любой точки пространства можно отложить вектор, равный данному, и притом только один.
Вспомним определения: Векторы называются равными, если они сонаправлены и их длины равны. И
Если векторы коллинеарны и при этом их лучи сонаправлены, то эти векторы называются сонаправленными.
Пусть нам дан вектор а и точка М. Проведем через вектор а и точку М плоскость. В этой плоскости построим вектор МК, равны вектору а. Очевидно, что вектор МК – искомый вектор. Из построения следует, что этот вектор единственный с началом в точке М и равный вектору а.
Решим задачу № 323.
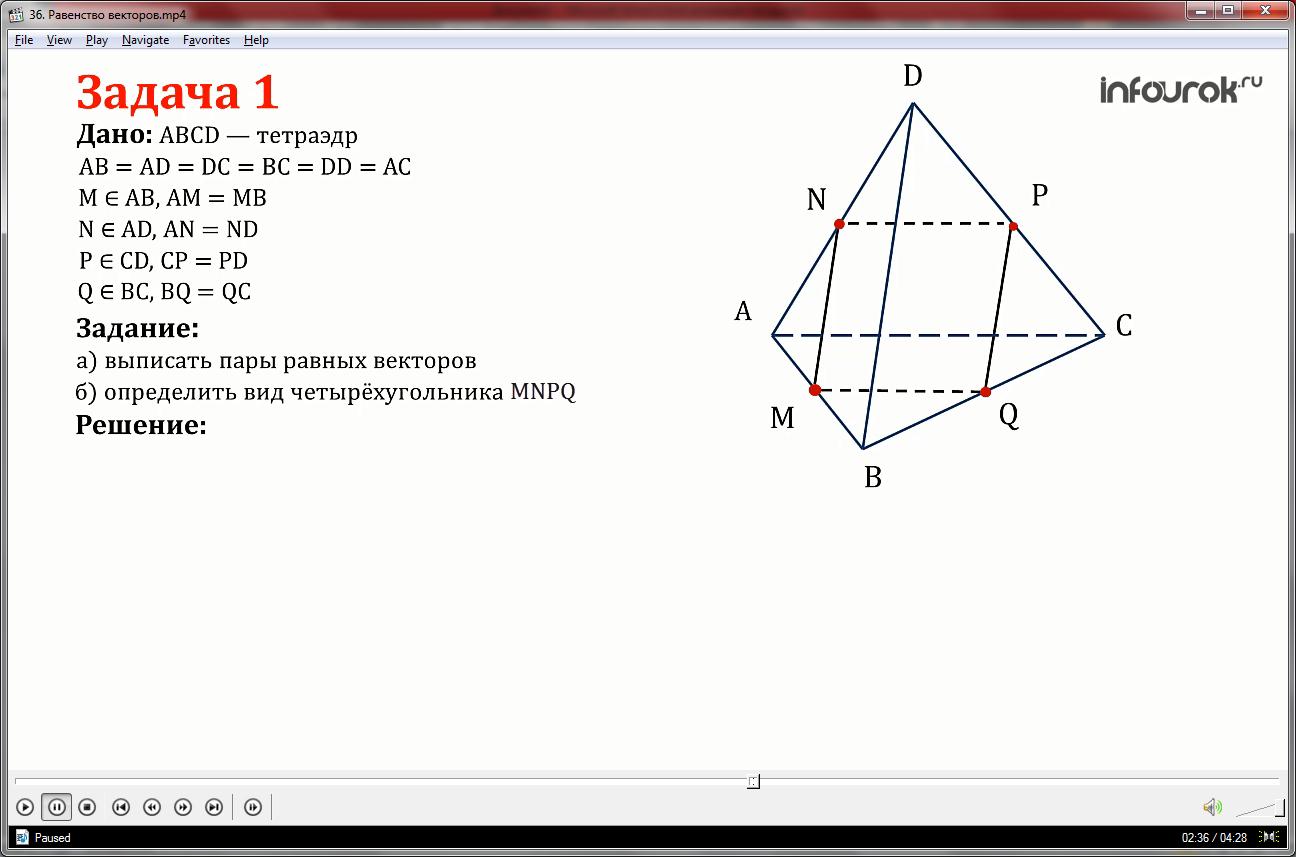
На рисунке изображен тетраэдр АВСD, ребра которого все равны. Точки М, N, P и Q – середины сторон
AB, AD, DC, BC. Необходимо выписать все пары равных векторов, изображенных на рисунке, и определить вид четырехугольника МNPQ.
Векторы равны, если они сонаправлены и их длины равны. Из условия задачи знаем, что точка Р середина DC,значит, отрезки DP и PC равны. Векторы DP и PC сонаправлены, а, значит, эти векторы равны.
NP-средняя линия треугольника ADC, значит, NP равно половинеAC и параллельно AC;
MQ-средняя линия тр. ABC, MQ равно половине AC и параллельно AC;
Значит, NP равно MQ, NP параллельно MQ. Из рисунка видим, что они сонаправленны. Векторы PN и QM равны.
PQ-средняя линия треугольника DВC; PQ равно половине DB и параллельно DB;
NM-средняя линия треугольника ADB, MN равно половине DB и параллельно DB. Делаем вывод, что вектор QP равен вектору MN.
Пары равных векторов: MN и QP, PN и QM, DP и PC.
Определим вид четырехугольника МNPQ. По условию все ребра тетраэдра равны, значит, он правильный и скрещивающиеся ребра в нем перпендикулярны.

Имеем: NP параллельно АС и параллельно QM.
MN параллельно DB и параллельно QP.
Отрезки MN, QP, PN и QM равны. Учитывая перпендикулярность DB и АС, можно сделать вывод, что MNPQ - квадрат. Задача решена.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7950 |
| Номер материала | 950 |