
Урок «Сложение и вычитание векторов»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем правило сложения двух векторов.
Пусть нам даны два неколлинеарных вектора a и b. Отложим от произвольной точки пространства А вектор АВ, равный вектору а. Затем от точки В отложим вектор ВС, равный вектору b. Вектор АС называется суммой векторов а и b.
Нужно отметить, что сумма векторов не зависит от выбора точки А.
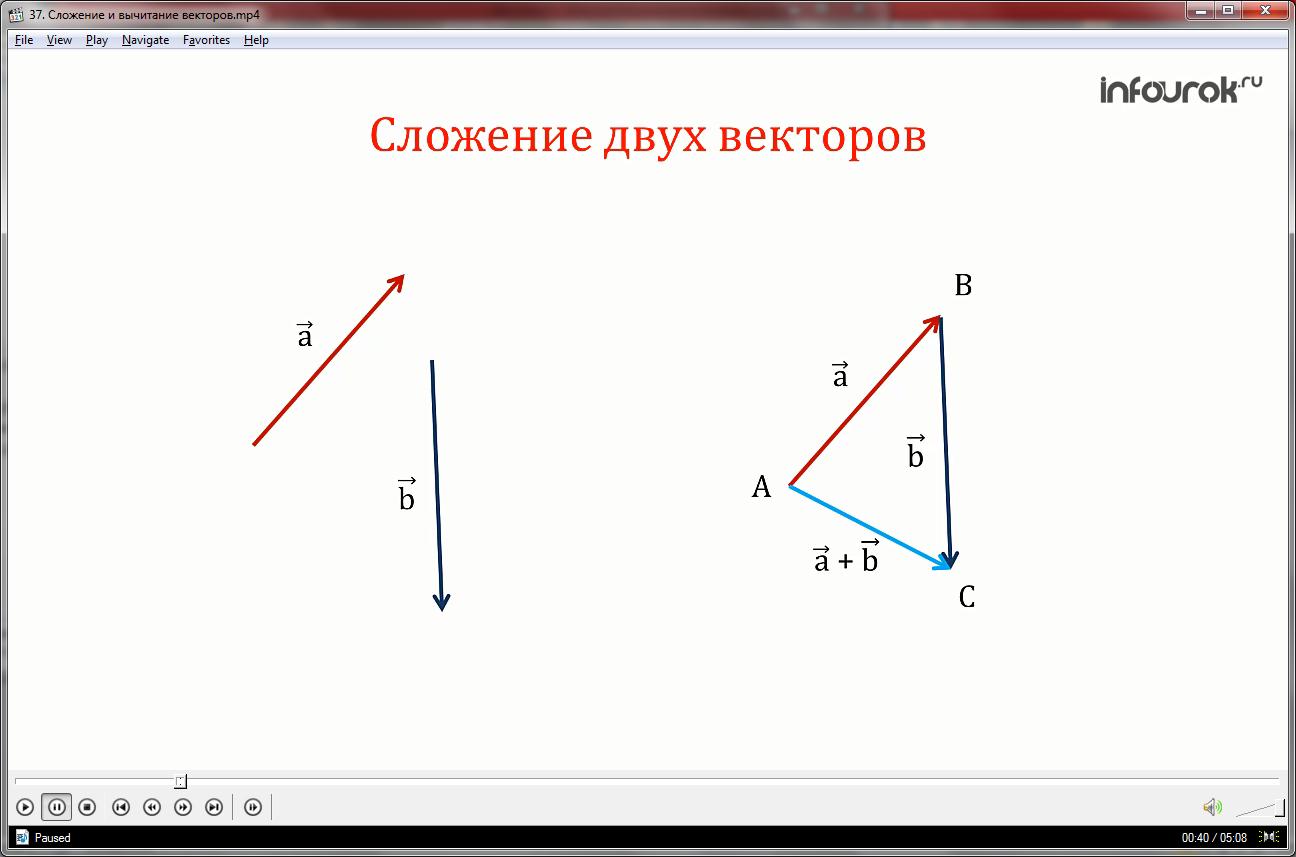
Это правило сложения векторов называется правилом треугольника.
Правило треугольника: для любых трёх точек А, В, С имеет место равенство: вектор АВ плюс вектор ВС получается вектор АС.
При сложении неколлинеарных векторов можно воспользоваться правилом параллелограмма.
Пусть даны векторы а и b. От произвольной точки А отложим векторы АВ и АС, равные соответственно а и b. Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b.
Решим задачу №327 под буквой а.
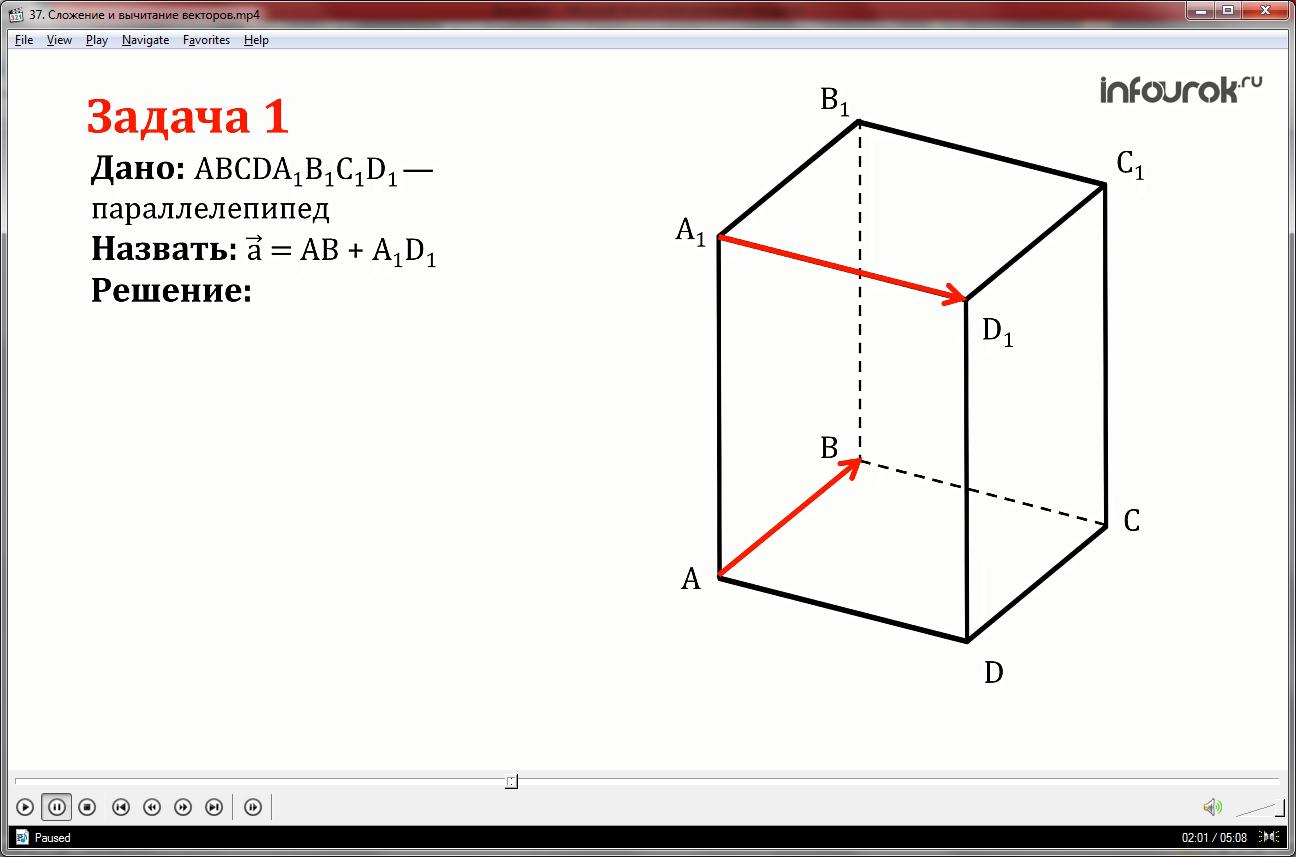
На рисунке изображен параллелепипед ABCDA1B1C1D1.Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов AB и A1D1 .
Воспользуемся правилом параллелограмма. К вектору АВ прибавим вектор АD, равный вектору A1D1.
Суммой этих векторов будет диагональ основания параллелепипеда, то есть вектор АС.
Напомним свойства сложения векторов, так как они ни чем не отличаются от свойств сложения векторов в планиметрии:
Для любых трех векторов а, бэ и це, выполняются равенства
1) переместительный закон
2) сочетательный закон
Введем определение противоположных векторов.
Два вектора называются противоположными, если их длины равны и они противоположно направлены
Вектор минус а противоположен вектору а
Вектор DF противоположен вектору FD, и равен минус вектор FD
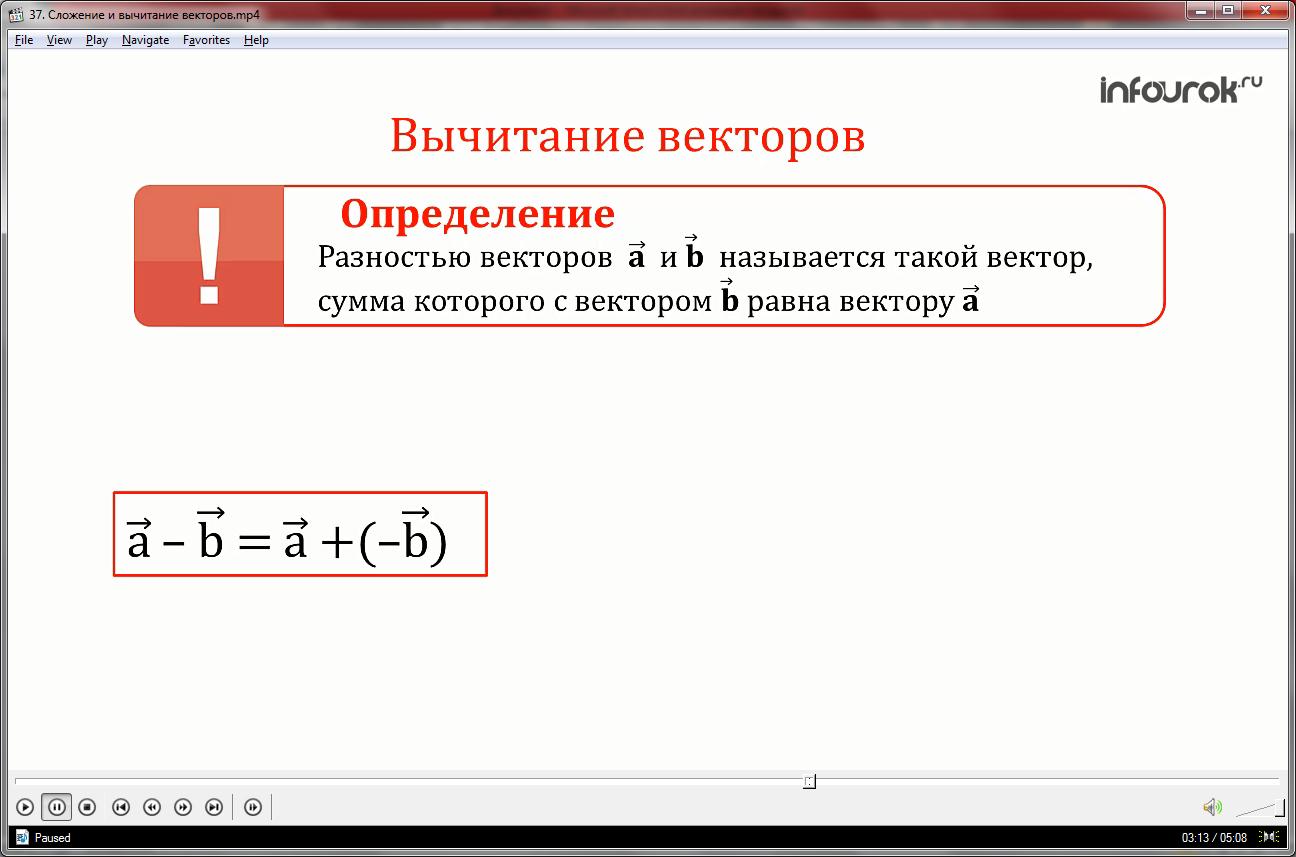
Определим вычитание векторов
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .
Разность векторов и можно найти как сумму вектора с противоположным вектором вектору .
Введем правило вычитания векторов.
Пусть нам даны два неколлинеарных вектора и . Отметим произвольную точку А. Отложим от точки А вектор АВ , равный вектору а и вектор АС, равный вектору b. Вектор СВ будет разностью данных векторов.
Существует правило для трех точек.
Любой вектор можно представить как разность двух векторов, проведенных из одной точки.
Добавляем третью точку (любую) и задаем разность из вектора, проведенного из этой точки в конец данного вектора минус вектор, проведенный в начало.
Решим задачу №332
На рисунке изображен параллелепипед ABCDA1B1C1D1 Представьте векторы АВ1 и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
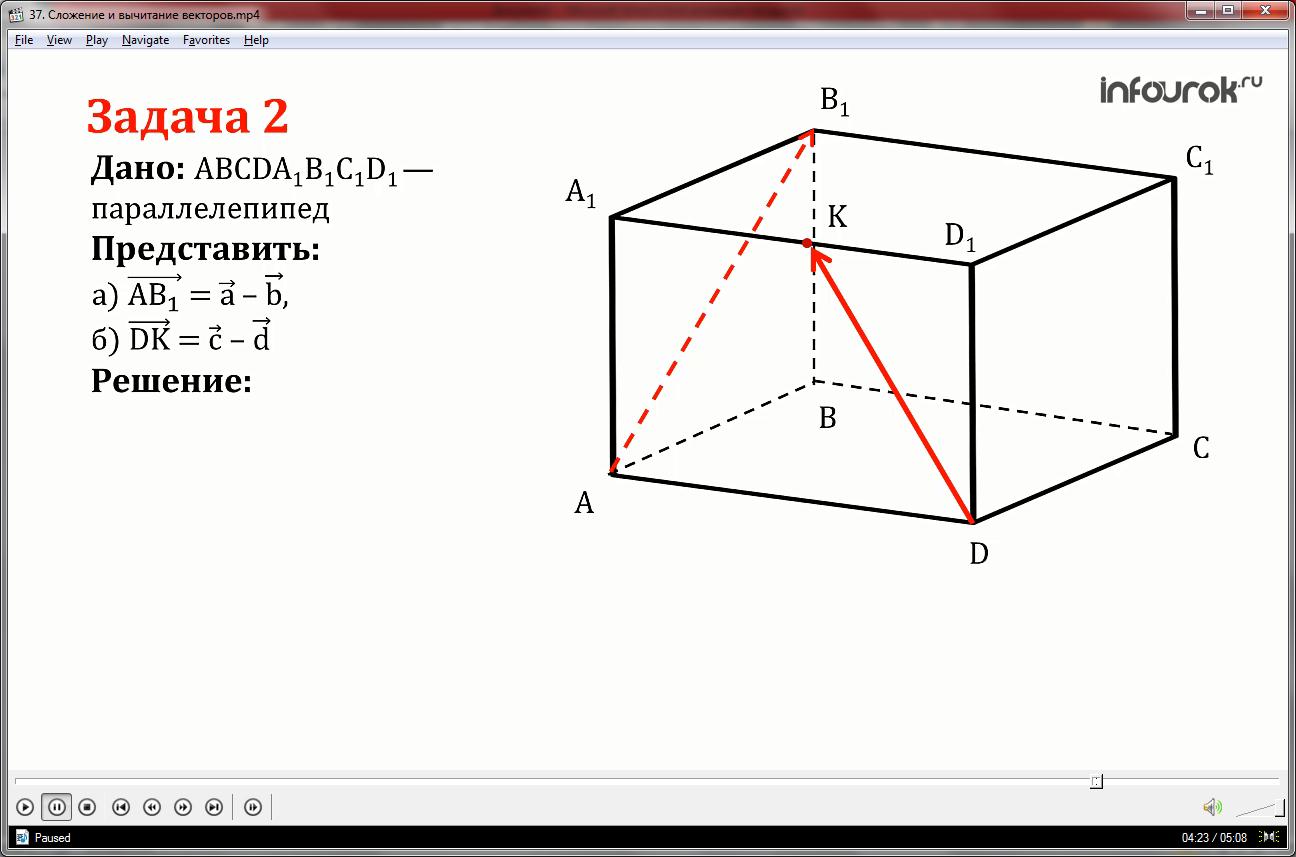
Решение.
Рассмотрим вектор АВ1 и воспользуемся правилом трех точек. Третьей точкой удобно взять точку А1. Вектор, проведенный в конец то есть в точку В1 будет А1В1 и в начало точку А – вектор А1А. Получаем АВ1 равно А1В1 минус А1А.
Выполним это же задание для вектора DK. Здесь третьей точкой удобно взять точку D1. Вектор в конец ¬ - D1K, в начало - D1D. Получим вектор DK равен D1K минус D1D.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11967 |
| Номер материала | 951 |