
Урок "Средняя линия треугольника"

Краткое описание документа:
Продолжая тему изучения треугольников и их свойств, предлагаем вашему вниманию презентацию. Она раскроет нам значение срединной линии треугольника, ее характеристики. Основной целью презентаций по геометрии является научить применять свойства геометрических объектов на практике.

Для начала познакомимся с самим общим понятием. В планиметрии выделяют такую характерную черту фигуры, как средняя линия, так называемый отрезок, соединяющий две стороны этой фигуры посередине. Это свойство также характерно для четырехугольника и трапеции, а не только для рассматриваемого объекта.
Как любая другая составляющая часть геометрической фигуры, средняя линия треугольника имеет свои особенные свойства. Первым обозначим то, что средняя линия параллельна третьей стороне треугольника и составляет половину ее длины. Далее, при проведении всех трех возможных средних линий, у нас получается четыре одинаковых треугольника, которые являются подобными с главным, но с половинным коэффициентом. А площадь треугольника, отсекаемого средней линией, равняется четверти площади основного треугольника.

Также выделяют основной признак этого свойства, который можно озвучить следующим образом: средней линией треугольника называют отрезок, в случае, когда он параллельный одной из сторон треугольника и соединяет середину одной стороны с точкой, которая лежит на второй стороне данной геометрической фигуры.
В подтверждение обозначенных характеристических свойств средней линии треугольника, презентация предлагает вашему вниманию доказательство этой теоремы. Она, то есть теорема, звучит следующим образом: средняя линия треугольника параллельна одной стороне и равна ее половине.
Сам рисунок представлен в презентации, к которой рекомендуем обращаться, следя за ходом доказательства. Итак, допускаем, что линия MN – средняя линия треугольника АВС. В ходе решения нужно доказать предложенные тезисы. Первый из них просит довести параллельность двух отрезков MN, которая является средней линией треугольника, предлагаемого нашей презентацией, и его стороны AC, которую отрезок MN не пересекает. Также необходимо будет доказать, что этот же отрезок составляет половину длины стороны треугольника.

Для начала, через точку N проводим прямую, которая параллельна стороне AC треугольника. Из следствий, вытекаемых из теоремы Фалеса, получается, что эта прямая проходит через середину AB, отрезок MN лежит на этой прямой. Первый тезис теоремы доказан. Сторона АВ относится к стороне ВМ, как и ВN относится к стороне ВС, как один к двум. Отрезок MN параллелен стороне АС, то есть МN относится к АС как один к двум, то есть MN равен одной второй от стороны АС.
Из чего следует, что теорема доведена.
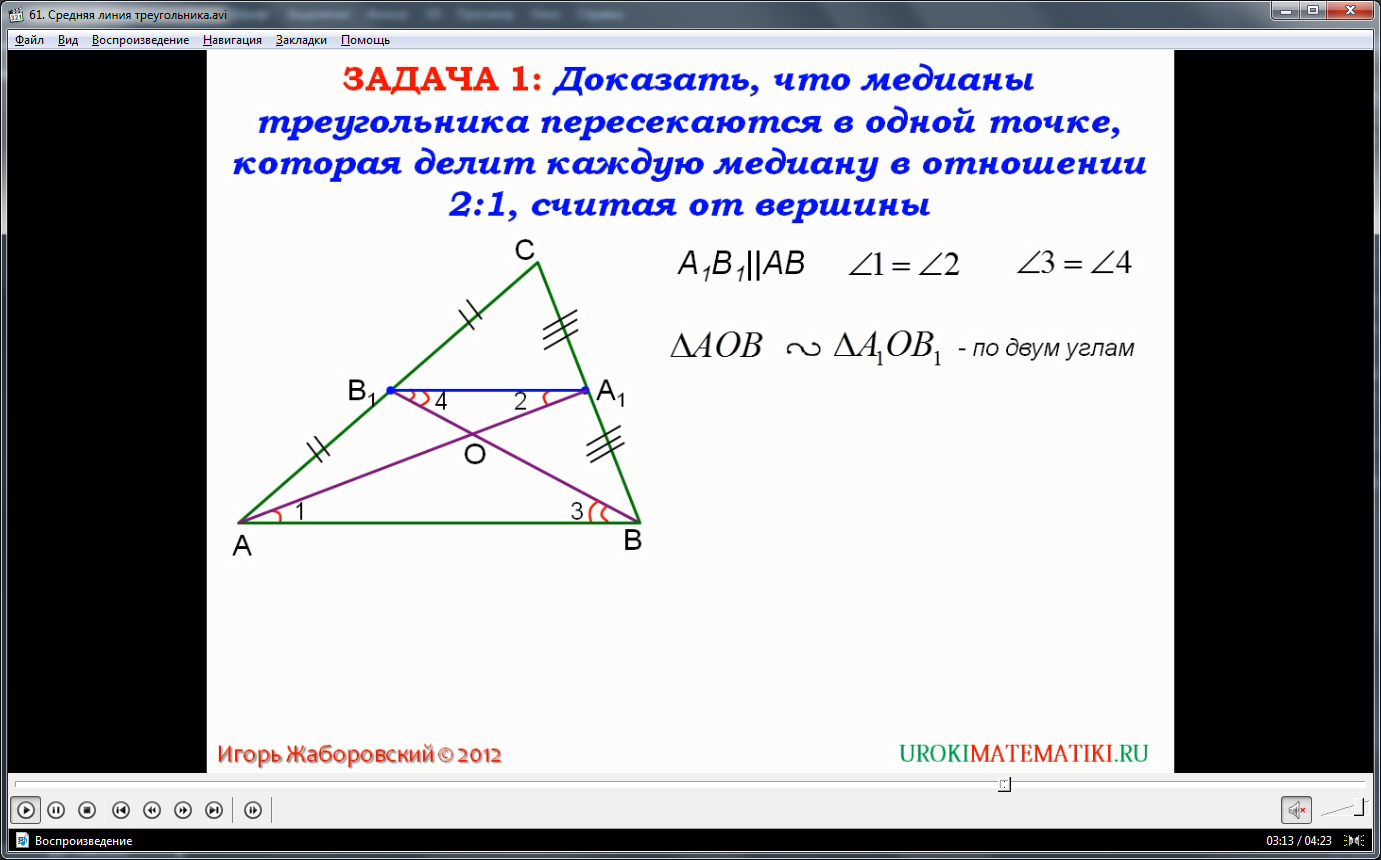
Также в презентации вы найдете еще одно из свойств средней линии треугольника и его доказательство. Рассмотрев и другие материалы, предложенные по данной теме, вы сможете понять и научиться применять на практике полученные вами знания.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5252 |
| Номер материала | 599 |