
Урок «Свойства функции»

Краткое описание документа:
Урок по теме «Свойства функции» рассчитан на 8:14 минут. За это время обучающиеся смогут познакомиться с основными понятиями по данной теме.
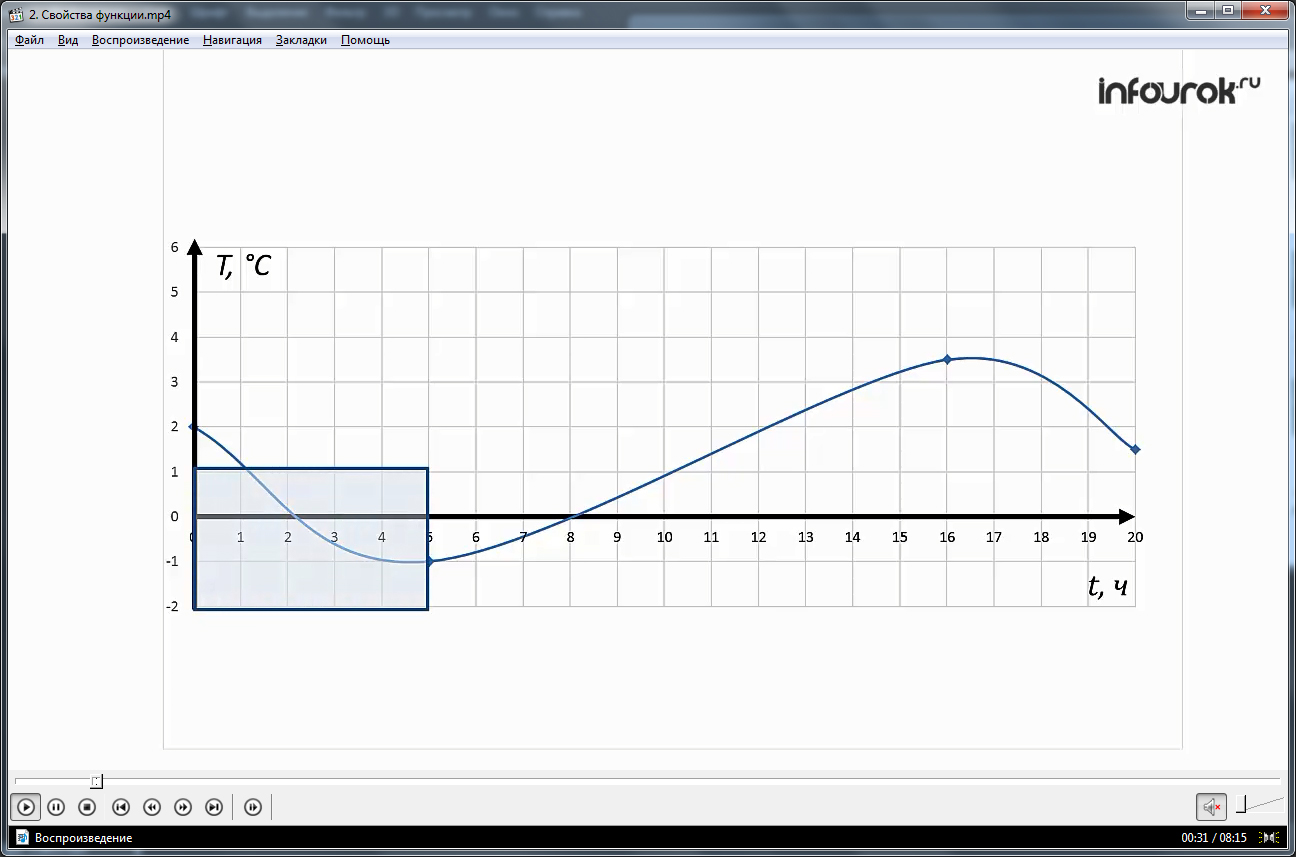
В начале урока, прежде, чем приступить к изучению свойств функции, автор предлагает рассмотреть примеры. Первый такой пример представлен в виде графика зависимости температуры воздуха от времени суток. На графике автор показывает, когда температура повышалась и понижалась. Так данный пример свидетельствует о том, что с помощью графика можно определить некоторые свойства функции.
Далее предлагается другой пример, где задана область определения функции. Необходимо определить, при каких значениях переменной функция положительно, отрицательно и равно нулю. Затем на экране демонстрируется график заданной функции. Автор подробно рассказывает, при каких значениях переменной функция имеет нулевое, положительное и отрицательное значения. При этом делается акцент на такое понятие, как нули функции. А затем отмечаются промежутки, где функция принимает положительные и отрицательные значения.
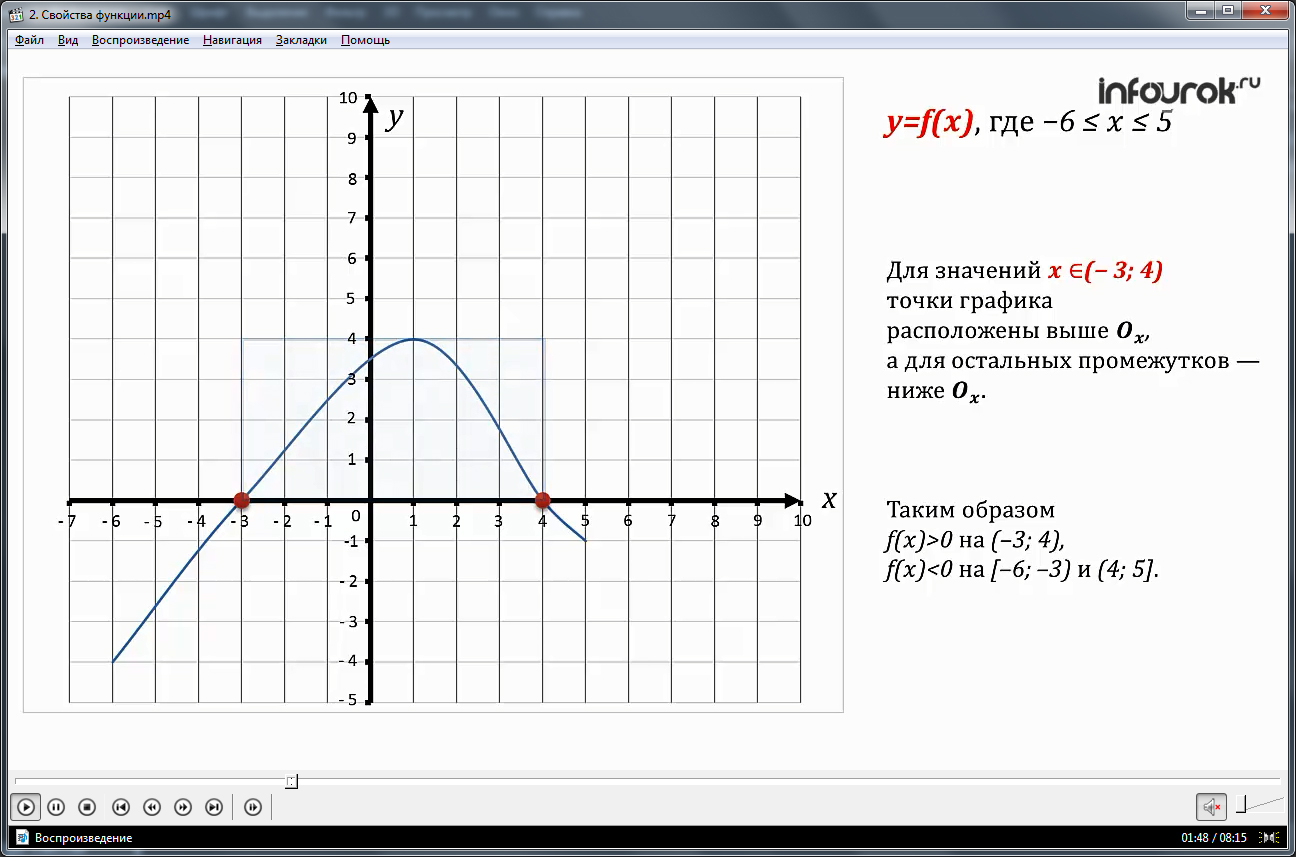
Далее автор вводит понятие промежутков знакопостоянства. После этого предлагается изучить, как изменяется значение функции с изменением значения переменной. При этом, автор возвращается к тому же графику. На графике видно, что на некоторых промежутках с возрастанием переменной значение функции увеличивается, а на других промежутках, наоборот, уменьшается. Так на примере вводятся понятия функции возрастающей и убывающей. Затем все вышесказанное обобщается, и на экране появляются определения возрастающей и убывающей функций. Эти определения выделены яркой рамкой, которая призывает запомнить определения.
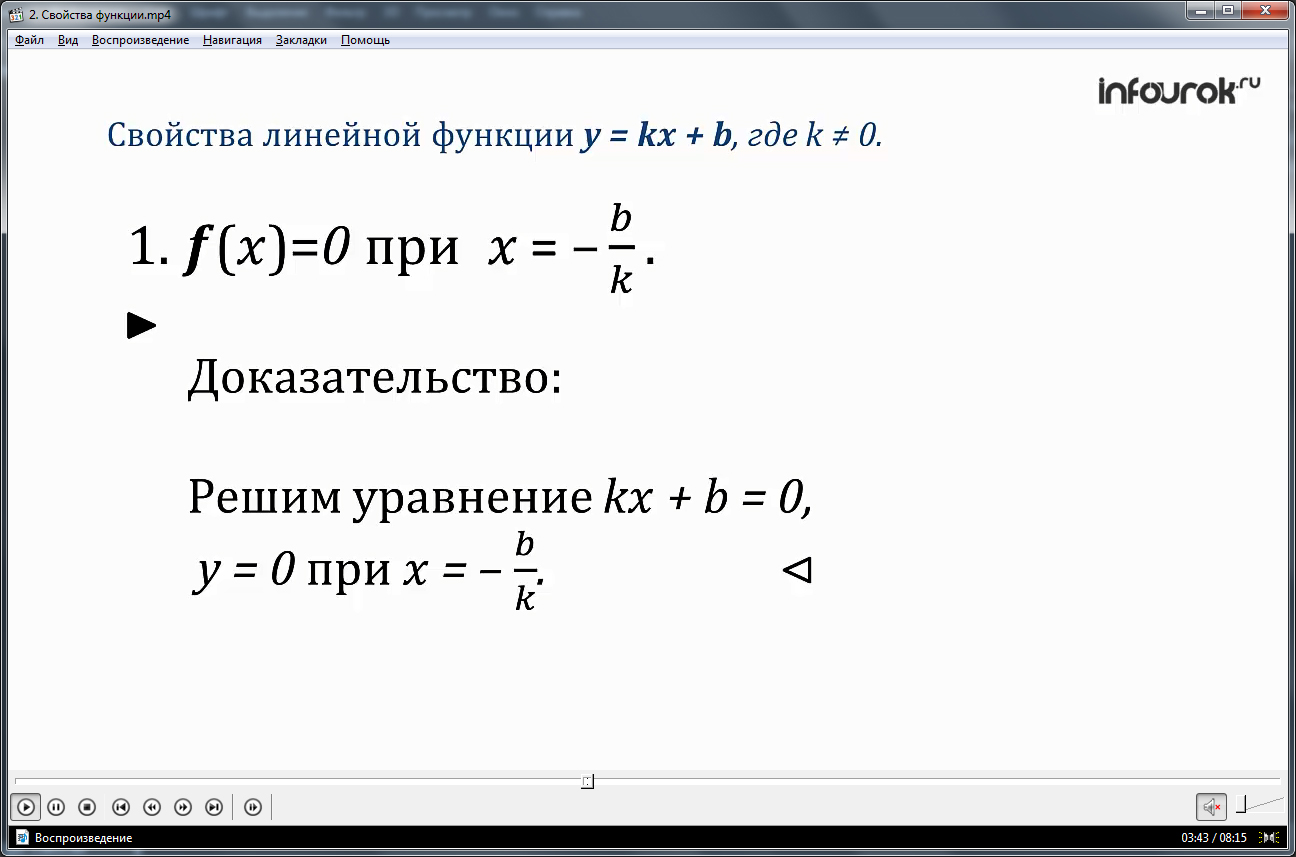
Далее на экране появляются два изображения графиков функций, одна из которых убывающая, другая – возрастающая. И тут же автор предлагает выяснить, какими свойствами обладают ранее изученные функции. И первой такой функцией является линейная. Первое свойство заключается в том, что находятся нули функции. Доказательство этого свойства также приводится на экране. Следующее свойство заключается в определении положительных и отрицательных значений функции. Доказательство этого свойства прилагается ниже. Третье свойство показывает, на каких промежутках функция является возрастающей и убывающей. После формулировки данного свойства на экране размещено его доказательство. Доказательства всех трех свойств автор раскрывает достаточно полно, все объясняется доступным и понятным языком, медленно и с необходимыми пояснениями.
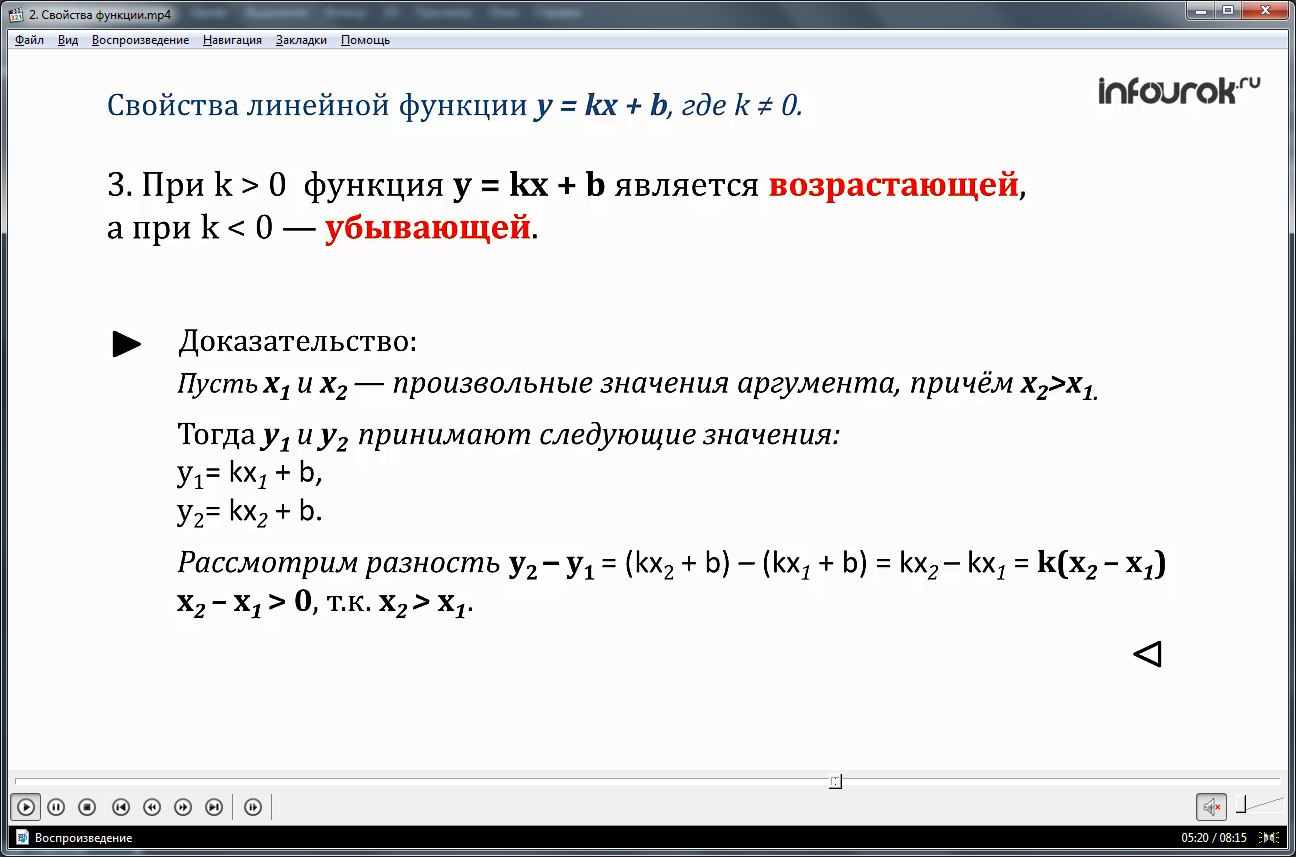
Затем рассматривается следующая функция. Для этой функции автор называет также три свойства: нули функции, промежутки, где функция положительна и отрицательна, промежутки возрастания и убывания. Первые два свойства приводятся с подробными и понятными доказательствами, а третье без него. Но автор поясняет, что это третье свойство доказывается подобно тому, как такое же свойство доказывалось для линейной функции. Это необходимо с целью экономии времени. После этого следует замечание, согласно которому школьники узнают, что функция не является убывающей или возрастающей на всей области определения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6570 |
| Номер материала | 690 |