
Урок "Свойство биссектрисы угла и серединного перпендикуляра к отрезку"

Краткое описание документа:
Треугольник – это одна из наиболее широко используемых фигур в геометрии. Существует множество задач, где затрагиваются свойства и законы этой элементарной фигуры. Поэтому в нашем видеокурсе уделяется особенное внимание тщательному анализу всех правил и теорем треугольника.
Для того, чтобы лучше усвоить материал нынешнего видео, следует напомнить и изучить основные понятия в данной отрасли.
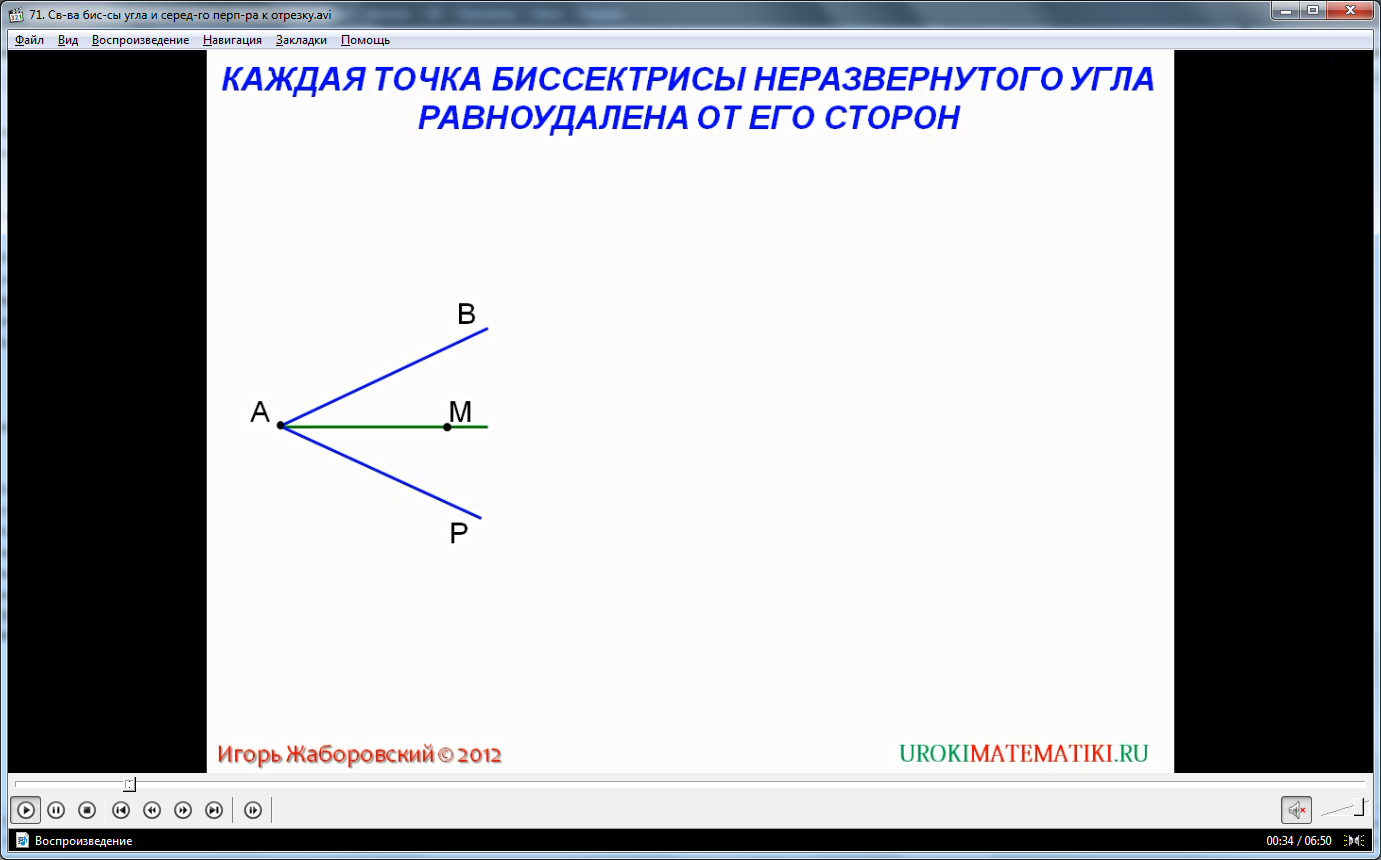
Биссектрисой любого угла треугольника является отрезок, исходящий из точки угла, и делящий этот угол ровно пополам. Срединным перпендикуляром в треугольнике называют отрезок, исходящий из точки, лежащей ровно посередине любой стороны, и пролегающий перпендикулярно данной стороне, то есть под углом в 90 градусов. Так как углов и сторон в треугольнике всего по три, то биссектрис и срединных перпендикуляров тоже можно провести по три.
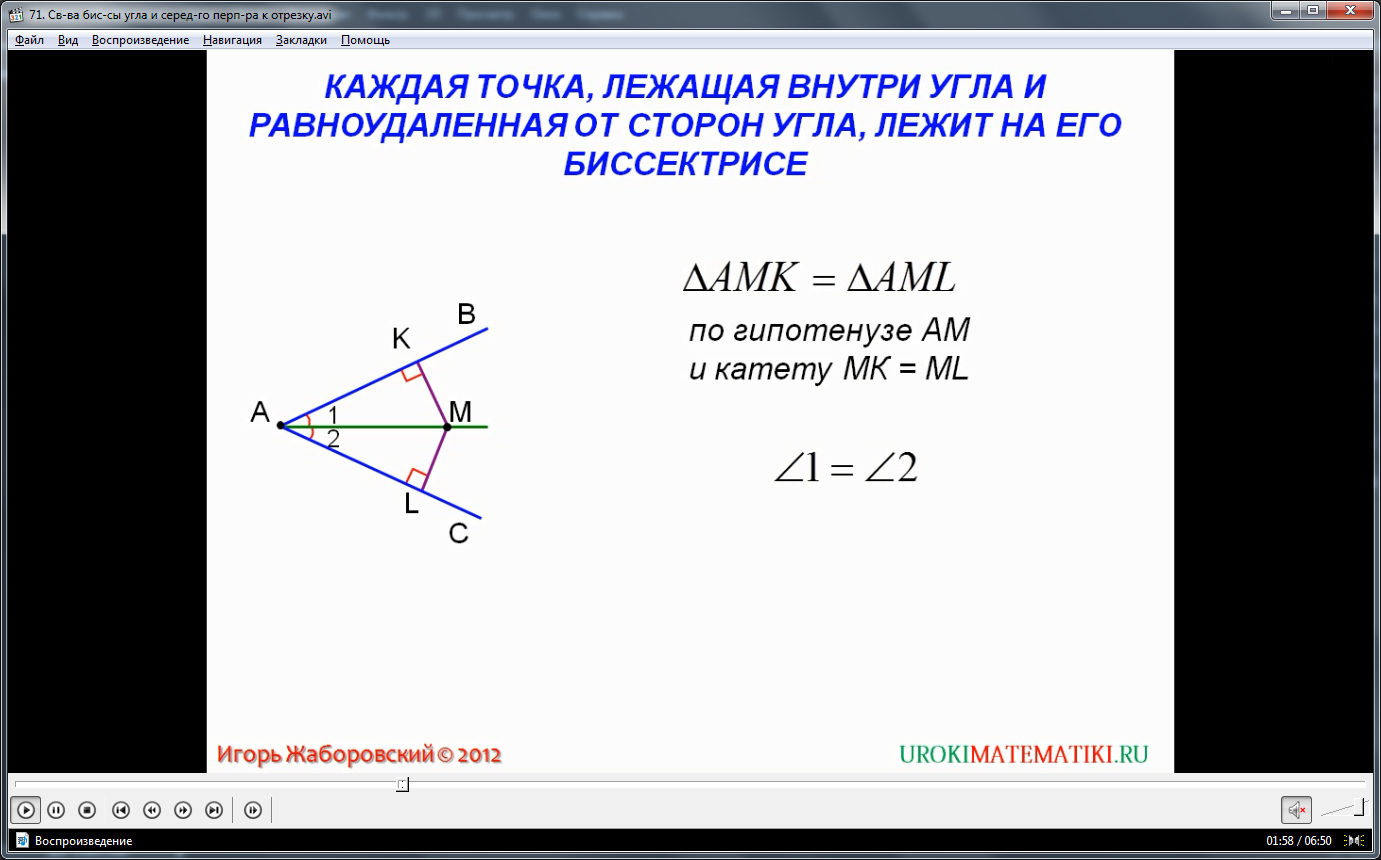
Стоит вставить ремарку, что определения данных отрезков не привязаны строго к треугольнику – они могут быть использованы не только в любой многоугольной фигуре, но и в простейших случаях, когда наличествуют только сам угол, или отрезок-сторона. Но, в представляемом видео, будут рассмотрены именно свойства биссектрис и срединных перпендикуляров в треугольнике.
В начале рассмотрим представленные простейшие геометрические казусы, помогающие усвоить основные определения сегодняшнего урока. Возьмем, к примеру, любой нешаровый угол МСР. Проведем в нем биссектрису ОС. По определению самой биссектрисы, угол МСО равен углу ОСР. Важнейшее свойство биссектрисы – любая точка, лежащая на ней, равноудалена от обеих сторон угла, в котором она основана. Пусть эта точка будет О, ближайшие точки на сторонах углов – Р и М. Треугольники РОС и МОС равны между собой, так как равны их прямые углы, общая гипотенуза ОС и острый угол ОСР и МСО (по определению биссектрисы). С этого свойства вытекает обратный, очевидный логически, вывод – любая точка, пролегающая внутри самого угла и равноудаленная от обеих его сторон, обязательно будет лежать на его гипотенузе. Доказательство этому идет по обратному типу – треугольники МОС и РОС равны между собой по гипотенузе, прямому углу и отрезкам МО и ОР, ведь у нас условие равноудаленности. Более широким следствием из данного свойства биссектрисы является тот факт, что все три биссектрисы любого плоского треугольника пересекаются в одной точке, относящейся к «замечательным» точкам треугольника. К примеру, рассмотрим треугольник АВС с биссектрисами СК, АМ, ВР. По свойствам равноудаленных точек биссектрис следует, что отрезки КО, ОР, ОМ абсолютно равны между собой.
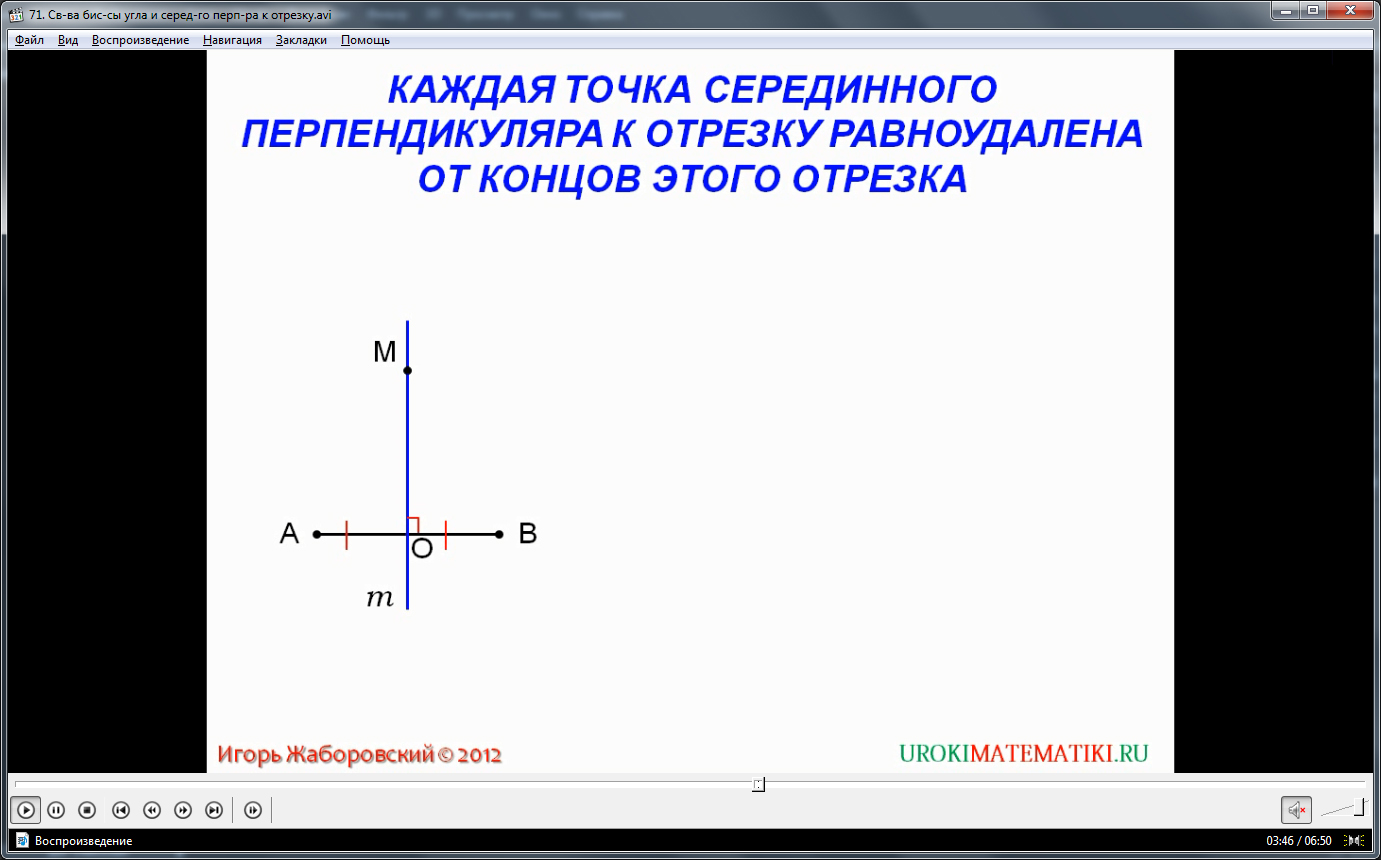
Далее, рассмотрим подробнее свойства срединного перпендикуляра. К примеру, есть у нас отрезок АС и срединный перпендикуляр к нему – Р1В, так что АР = РС, а углы ВРС = ВРА = 90 градусам. Главное правило этого перпендикуляра – любая точка, лежащая на нем, равноудалена от концов отрезка, т.е. в данном случае, от А и С. Обратное следствие: если точка лежит равноудаленно от концов определенного отрезка, то точка пролегает на срединном перпендикуляре этого отрезка. В применении к нашей иллюстрации – точка В или точка О лежат на срединном перпендикуляре ВР1, при этом АО = ОС, АВ = ВС. Доказательства этих свойств вытекают из сравнения треугольников АВР и ВРС – они являются прямоугольными и равными по общей гипотенузе и острому углу.

Следствие для треугольника: в любом треугольнике все срединные перпендикуляры пересекаются в одной точке. Вывод этого правила несложен – если рассмотрим треугольник АВС со срединными перпендикулярами ВР1, АМ1, СК1, увидим, что некоторые внутренние треугольники равны между собой. КОА = КОВ, ВМО = МОС, АОР = РОС по общим гипотенузам и острому углу. Таким образом, ВО = ОА = ОС, где О – центр пересечения срединных перпендикуляров.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8692 |
| Номер материала | 609 |