
Урок «Теорема о прямой, перпендикулярной к плоскости»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
В начале изучения сегодняшней темы, мы разберём задачу на применение некоторых теорем о перпендикулярности прямых и плоскостей
Вспомним их: Первая теорема Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна двум пересекающимся прямым лежащим в плоскости, то она перпендикулярна к этой плоскости.
И две теоремы о параллельных прямых прямая теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
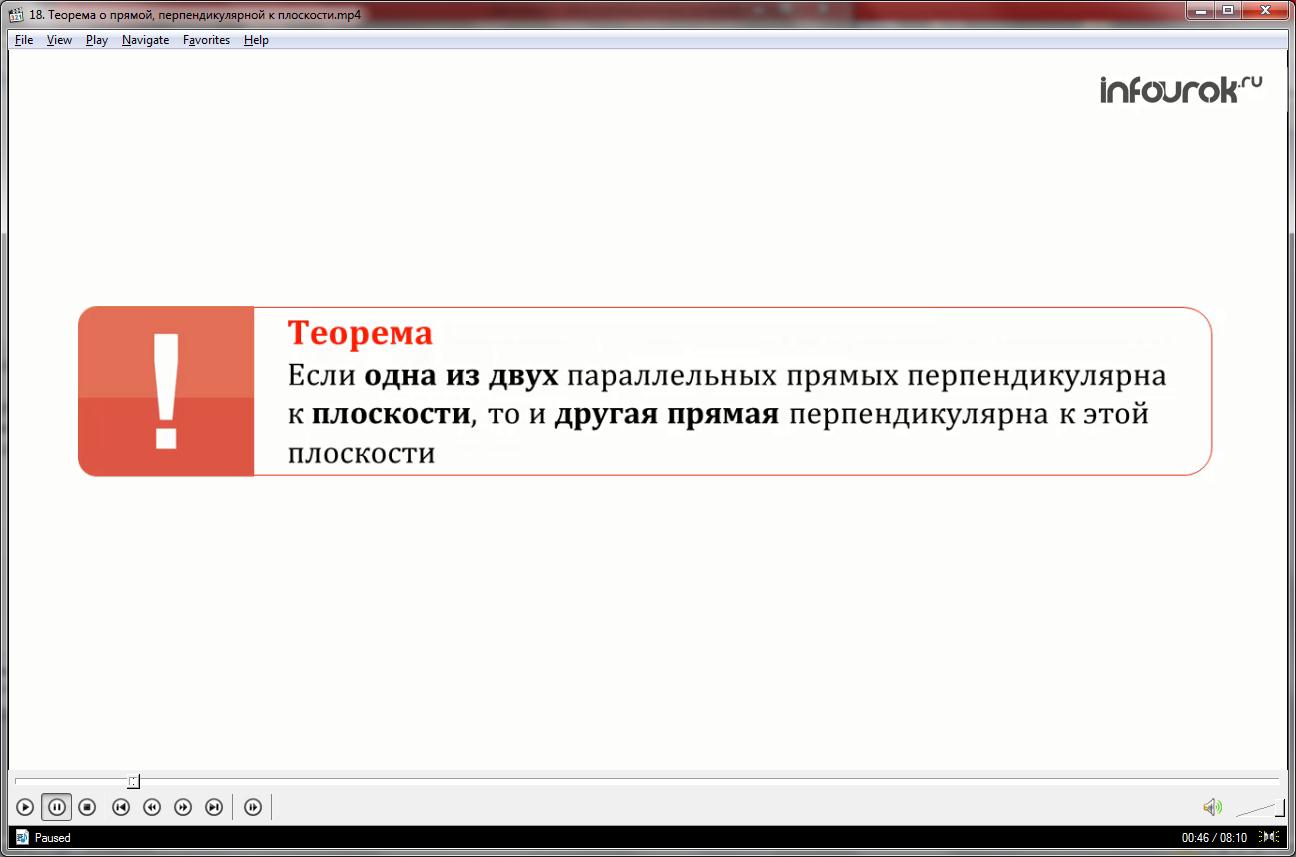
И обратная теорема . Если две прямые перпендикулярны к плоскости, то они параллельны. Доказательство этих теорем мы уже с вами разбирали.
Рассмотрим задачу на доказательство.
Задача.
Доказать, что через любую точку пространства проходит плоскость, перпендикулярная данной прямой.
Для решения рассмотрим прямую а, и произвольную точку пространства –точку М. Докажем, что существует плоскость, проходящая через точку М и перпендикулярная к прямой а.
Для доказательства проведем две плоскости α и β содержащие прямую а, так как это их общая прямая, значит прямая а их линия пересечения.
В плоскости β через точку М проведем прямую b перпендикулярную к прямой а. пусть эти прямые пересекаются в точке О.
В плоскости α проведём прямую с, проходящую через точку О и перпендикулярную прямой а.
По теореме о существовании плоскости, а именно через две пересекающие прямые в и с можно провести плоскость и при том только одну.
Рассмотрим плоскость γ (гамма), проходящая через прямые с и b.
Плоскость γ(гамма) будет искомой плоскостью, так как прямая а перпендикулярна двум пересекающимся прямым в и с
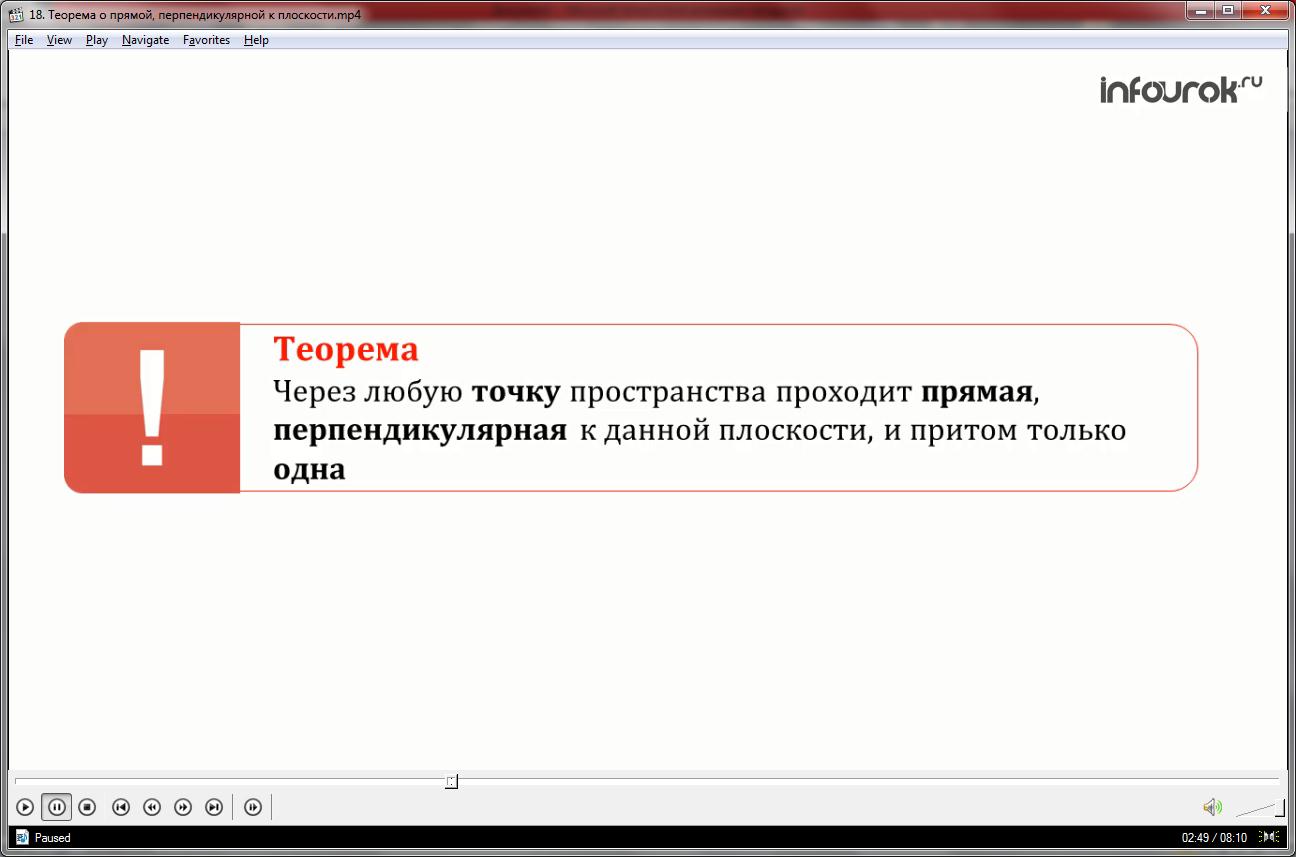
Данная задача демонстрирует существование плоскости перпендикулярной данной прямой. Рассмотрим теорему, утверждающую о существовании и единственности прямой перпендикулярной к данной плоскости.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Рассмотрим плоскость α и произвольную точку пространства – точку А.
Докажем, что через точу А проходит единственная прямая, перпендикулярная к данной плоскости.
1,2) Итак, проведем в плоскости α произвольную прямую m. Построим плоскость так что бы она проходила через точку А перпендикулярно к прямой m.
3,4)Пусть плоскость α и β пересекаются по прямой n. В плоскости β, через точку А проведём прямую р, перпендикулярно прямой n.
5) Прямая т, перпендикулярна плоскости β, значит перпендикулярна любой прямой в этой плоскости, то есть прямая т перпендикулярна прямой р.
6) Тогда прямая p перпендикулярна двум пересекающимся прямым m и n, лежащими в плоскости α, следовательно по признаку перпендикулярности прямой и плоскости прямая p перпендикулярна плоскости α.
7) Важно понимать, что такая прямая может быть только одна. Если бы через точку А проходило две прямых, например, ещё прямая p1, перпендикулярная плоскости α. Но две прямые перпендикулярные одной плоскости параллельны, что противоречит нашему предположению. Таким образом, через точку пространства проходит только одна прямая перпендикулярная данной плоскости.
Это утверждение в геометрии носит название теоремы о прямой, перпендикулярной к плоскости.
Задача
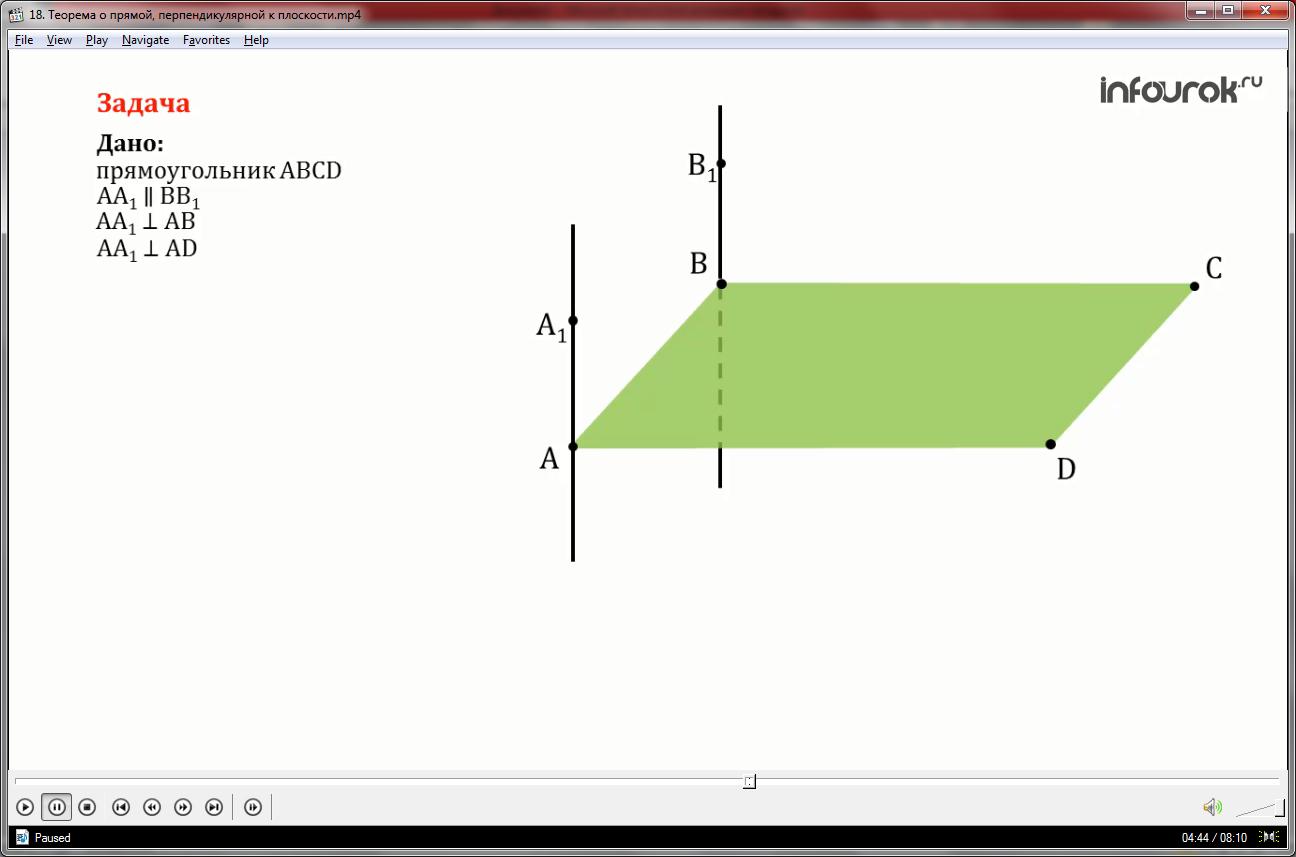
Через вершины А и В прямоугольника АВСD проведены параллельные прямые АА1 и ВВ1 не лежащие в плоскости прямоугольника. Известно, что АА1 АВ и АА1 АD. Найдите ВВ1, если В1D=25 см, АВ=12 см, AD=16 см.
Решение.1) Так как прямая АА1 перпендикулярна двум пересекающимся прямым AD и АВ лежащим в плоскости прямоугольника, то признаку
перпендикулярности прямой к плоскости АА1 перпендикулярна к плоскости АВСD.
2) Прямая ВВ1 параллельна прямой АА1 следовательно по теореме и прямая ВВ1 перпендикулярна к плоскости АВСD, и перпендикулярна любой прямой лежащей в этой плоскости, то есть ВВ1 перпендикулярна к прямой ВD. Значит треугольник В1ВD прямоугольный.
3) Из прямоугольного треугольника ВAD по теореме Пифагора квадрат гипотенузы BD равен сумме квадратов катетов АВ и AD и BD равняется 20 см.
4)По теореме Пифагора из прямоугольного треугольника В1ВD. Квадрат катета В1В равен разности квадратов гипотенузы В1D и известного катета BD , и катет равен 15 см.
Рассмотрим задачу на доказательство.
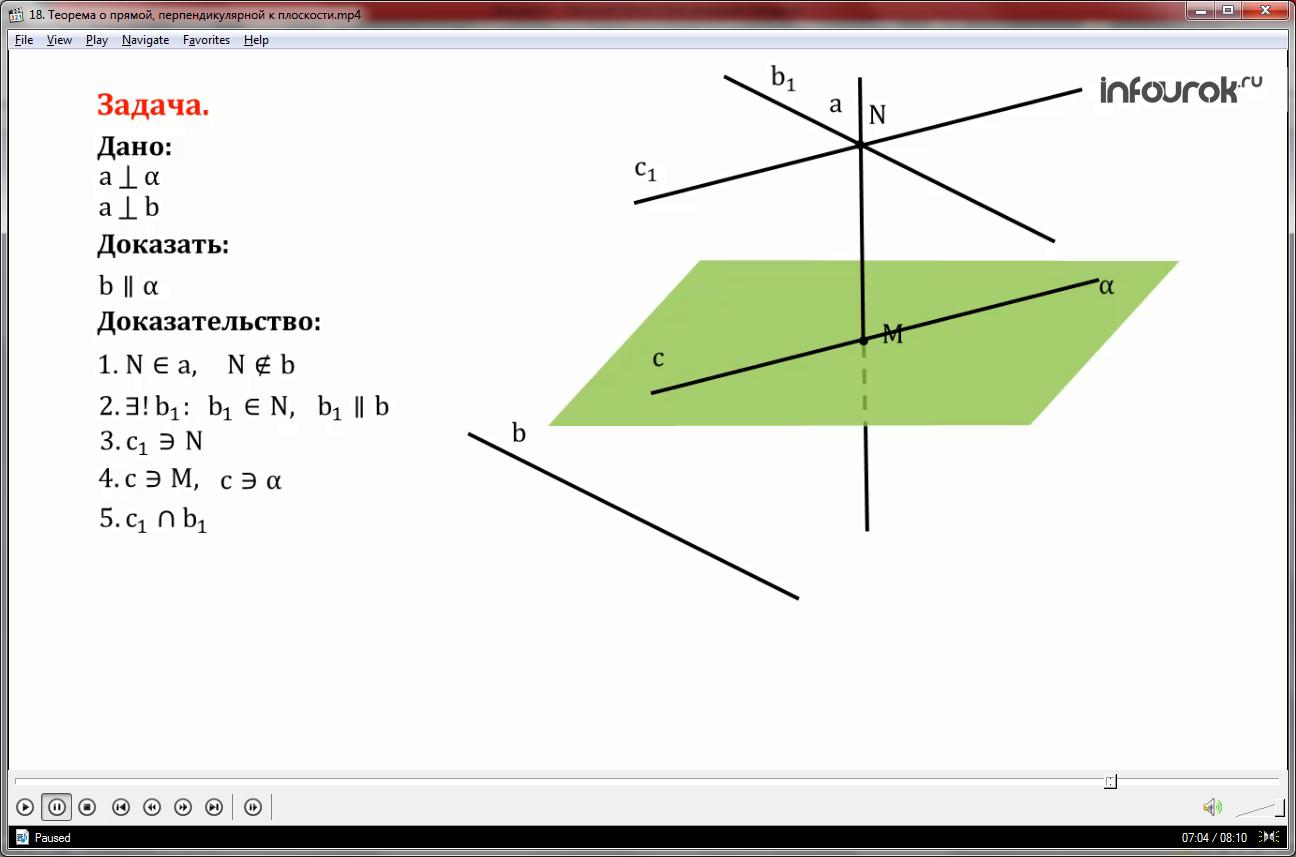
Прямая а перпендикулярна к плоскости α и перпендикулярна к прямой b, не лежащей в этой плоскости. Докажите, что b||
Назовём точку пресечения прямой и плоскости-точкой М.
1,2) Отметим на прямой а некоторую точку N не лежащую на прямой b. Через точку не лежащую на данной прямой можно провести единственную прямую параллельную данной. Пусть этой прямой будет прямая b1.
3) Через точку N проведём прямую с1.
4)Через точку М в плоскости α проведём прямую с параллельную прямой с1.
5)Через две пересекающие прямые с1 и b1 можно провести плоскость β согласно теореме о существовании плоскости.
6) Прямая а перпендикулярна по условию плоскости α, значит перпендикулярна прямой с, лежащей в плоскости, но с параллельна прямой с1, следовательно прямая а перпендикулярна прямой с1.
7,8) Аналогично прямая а перпендикулярна прямой b по условию, прямая b параллельна прямой b1, следовательно, прямая а перпендикулярна прямой b1. Значит прямая а, по признаку перпендикулярности прямой и плоскости, перпендикулярна плоскости β.
9)Плоскости α и β перпендикулярны прямой а, значит они параллельны.
10) Прямая b параллельна прямой b1, значит она параллельна плоскости β, и параллельна плоскости α.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 18509 |
| Номер материала | 932 |