
Урок «Теорема о трёх перпендикулярах»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
На прошлых занятиях вы уже познакомились с такими понятиями как: перпендикуляр к плоскости, наклонная, проекция, расстояние от точки до плоскости.
А теперь попробуем провести прямую через основание наклонной перпендикулярно её проекции. Что можно сказать о данном перпендикуляре?
Если в плоскости провести прямую через основание наклонной перпендикулярно к её проекции на данную плоскость, то эта прямая будет перпендикулярна и к самой наклонной.
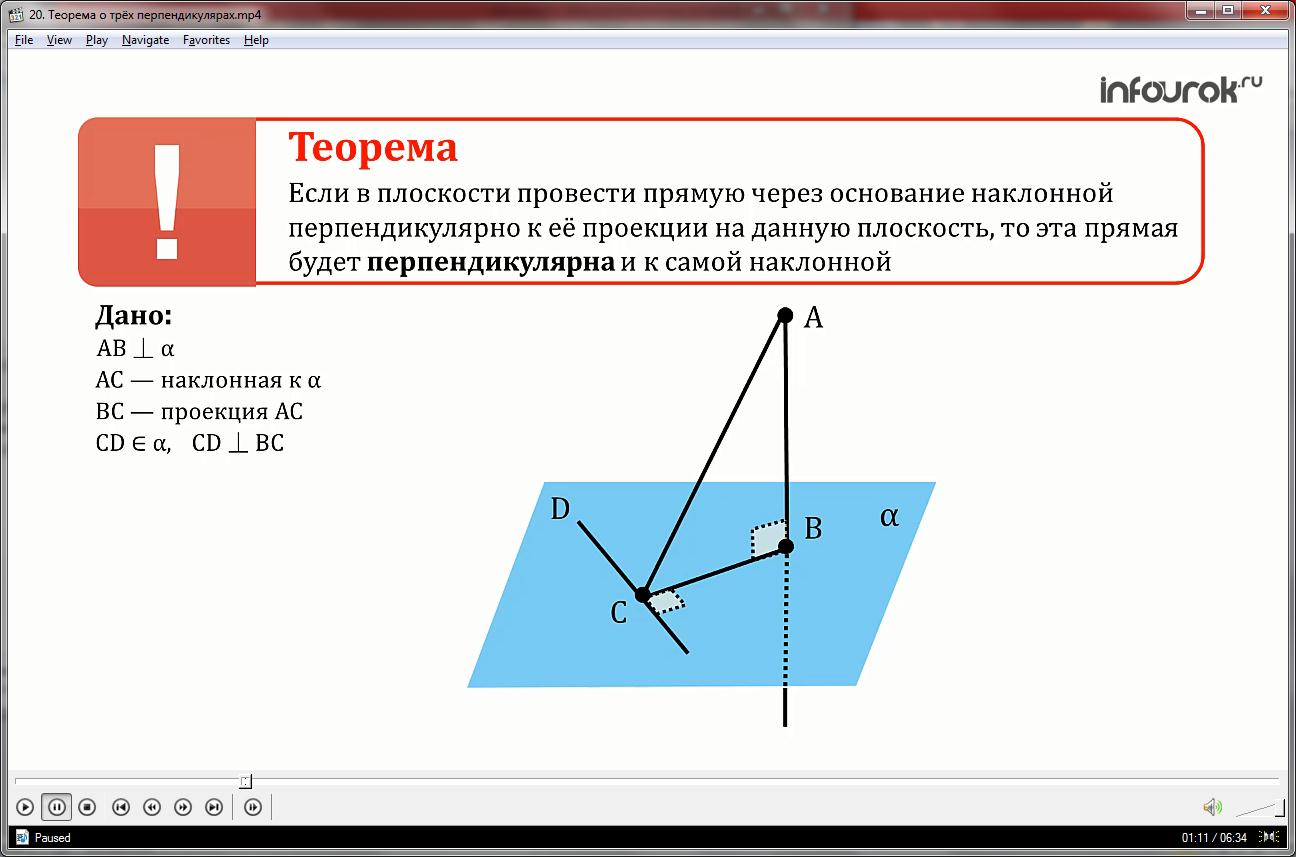
Докажем, что прямая ДС перпендикулярна прямой АС:
1.Известно, что прямая АВ перпендикулярна плоскости α, АС-наклонная к плоскости α, ВС-проекция наклонной АС, прямая СД принадлежит плоскости альфа, а так же прямая СД перпендикулярна прямой ВС по построению.
2.Рассмотрим плоскость АСВ: прямая ДС перпендикулярна прямой ВС по условию, а так как прямая АВ перпендикулярна плоскости альфа, значит прямая АВ будет перпендикулярна и прямой ДС, лежащей в этой плоскости (по теореме о перпендилурности прямой и плоскости).
3.Прямая СД перпендикулярна к двум пересекающимся прямым АВ и ВС, принадлежащим плоскости АВС, значит прямая будет перпендикулярна и самой плоскости АВС-по признаку перпендикулярности прямой и плоскости.
4.Из признака перпендикулярности прямой и плоскости следует, что прямая ДС перпендикулярна к любой прямой, лежащей в плоскости АВС, значит прямая ДС перпендикулярна прямой АС.
Таким мы образом мы доказали, что прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярная к самой наклонной.
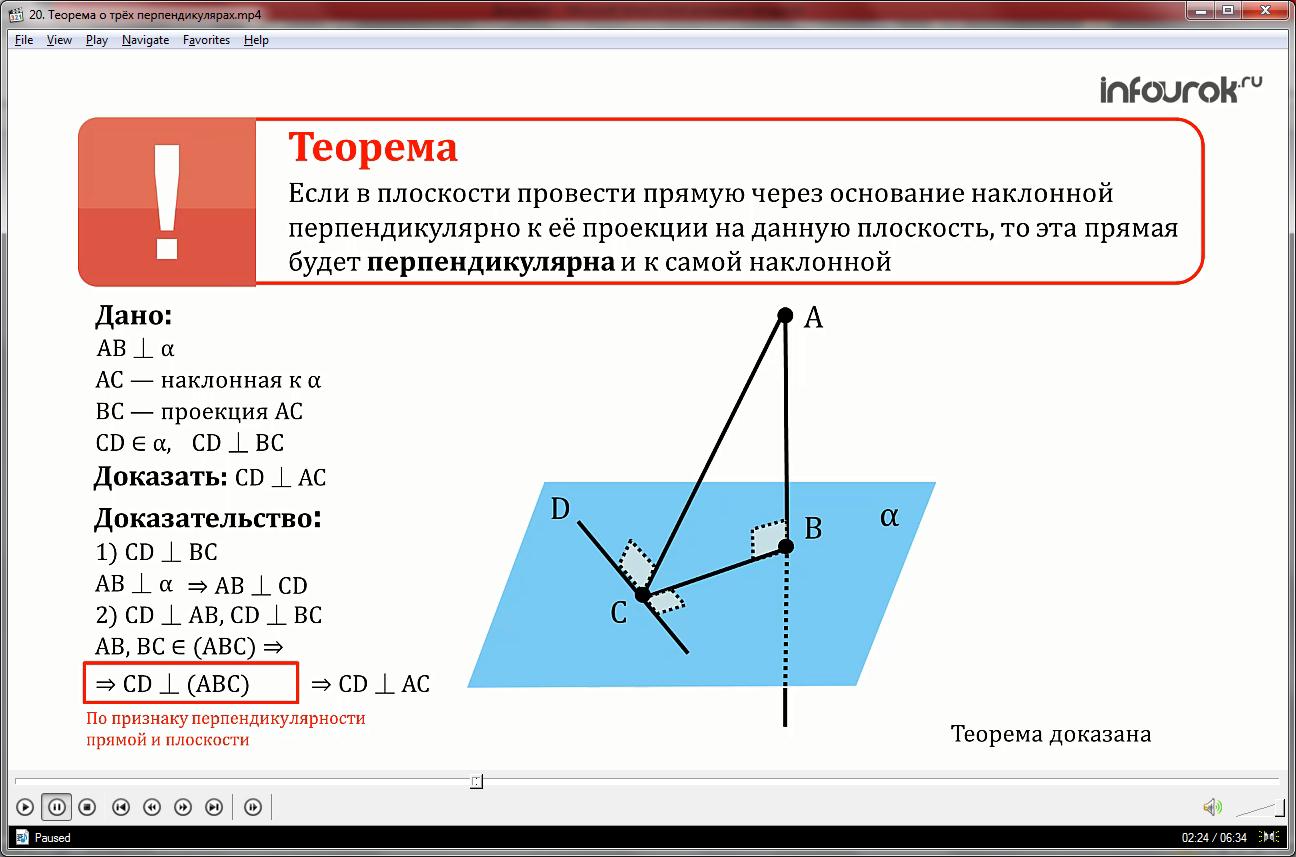
Доказанное утверждение называется теоремой о трёх перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АВ, ДС и ВС.
Существует так же и обратная теорема:
Если провести прямую в плоскости через основание наклонной перпендикулярно к ней, то данная прямая будет перпендикулярна и к ее проекции.
Докажите эту теорему самостоятельно.
Рассмотрим применение теоремы о трех перпендикулярах при решении задач.
Задача1.
Отрезок АД перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ =АС=5 см, ВС=6 см. АД=12 см.Найти расстояние от концов отрезка АД до прямой ВС.
Решение:
1.Дополнительное построение: проведем АЕ перпендикулярно ВС. Отрезок АЕ и будет расстоянием от точки А до прямой ВС.
2. Так как треугольник АВС равнобедренный, то АЕ является высотой и медианой, значит ВЕ=ЕС=3 см
3.Так как треугольник АЕС прямоугольный, то АЕ можем найти по теореме Пифагора:
АЕ= АЕ=√52-32, АЕ=4 см.
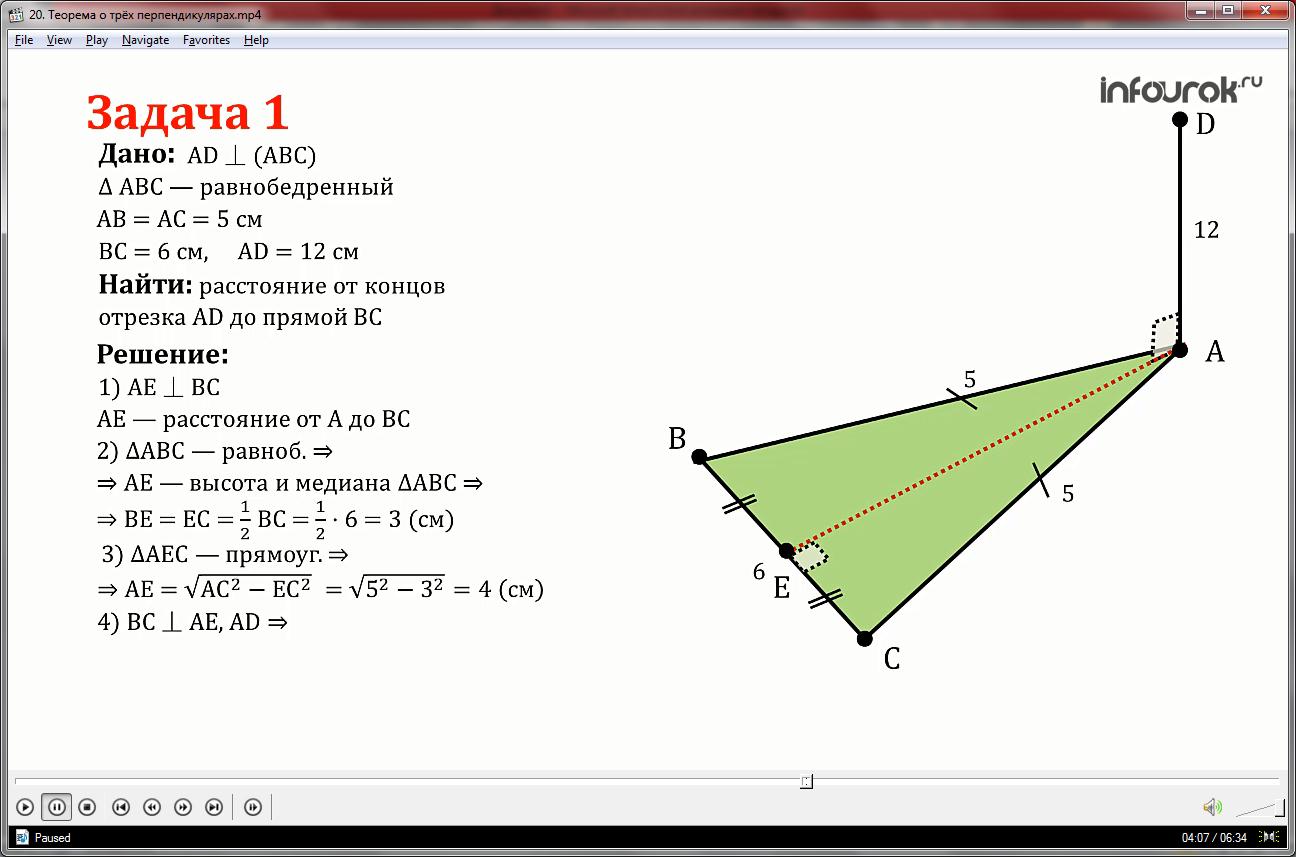
4.Отрезок ВС перпендикулярен АЕ, вместе с тем отрезок ВС перпендикулярен DА(по признаку перпендикулярности прямой и плоскости), тогда по теореме о трех перпендикулярах ВС перпендикулярен DЕ.
5.Из прямоугольного треугольника ДАЕ найдем ДЕ по теореме Пифагора: ДЕ=√АЕ2+АД2, DЕ=√42+122=√160=4√10 см.
Задача 2
Прямая ВД перпендикулярна к плоскости треугольника АВС. Известно, что ВД=9см, АС=10 см, ВС=ВА=13 см.Найти расстояние а)от точки Д до прямой АС
б)площадь треугольника АСД.
Решение:
1.Проведём ВЕ перпендикулярно АС.
2.Так как Треугольник АВС равнобедренный, то ВЕ –высота и медиана, значит СЕ=ЕА=5 см.
3.ВД перпендикулярна АС, ВЕ перпендикулярна АС, то по теореме о трёх перпендикулярах ДЕ перпендикулярна АС.
4.Расстояние от точки Д до прямой АС это отрезок ДЕ. Так как треугольник ВЕД прямоугольный, то по теореме Пифагора
ДЕ=√ВЕ2+ВД2.
В свою очередь ВЕ можно найти из прямоугольного треугольника СВЕ:
ВЕ=√ВС2-ЕС2=√132-52=√169-25=12 см.
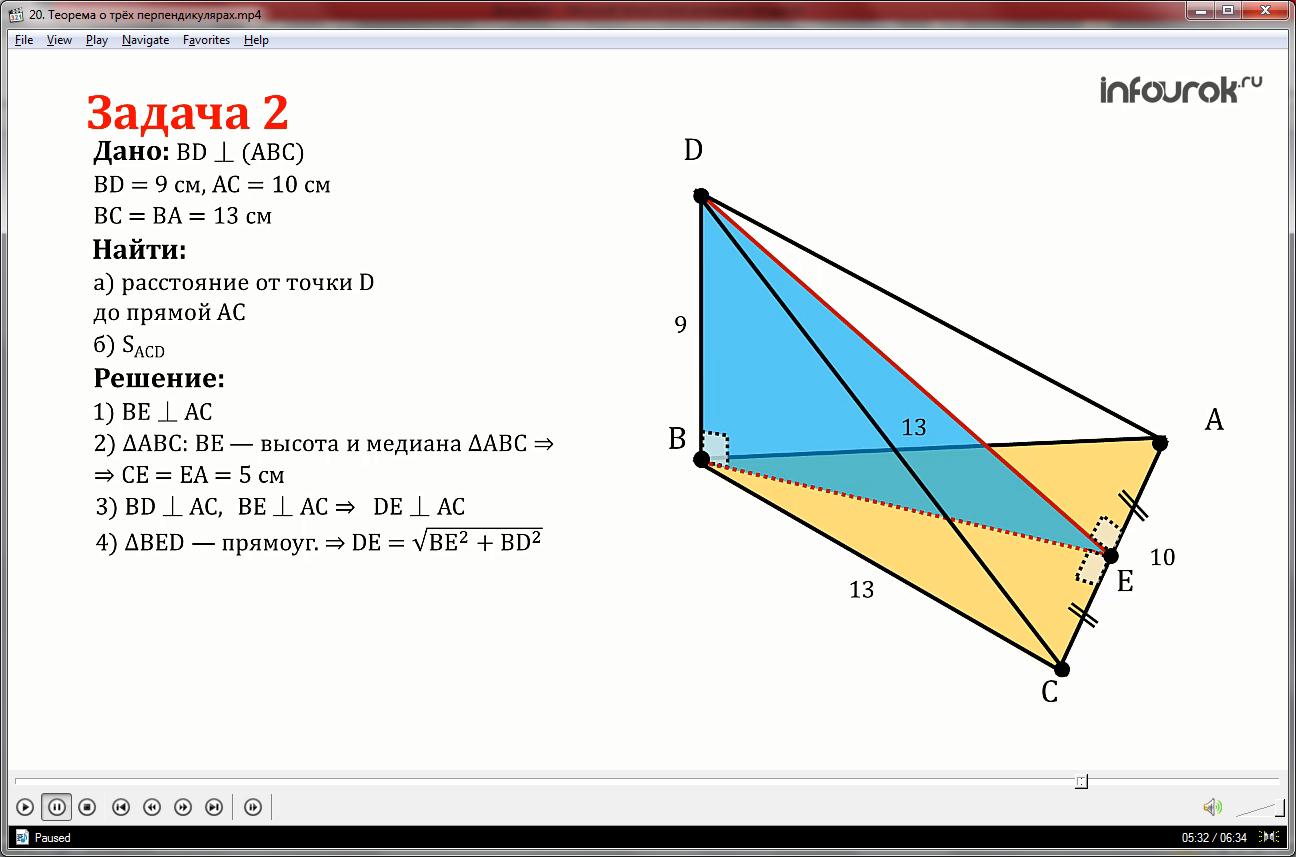
Тогда ДЕ=√122+92=√144+81=15 см
5.В треугольнике АСД: АС-основание, ДЕ-высота, тогда по формуле нахождения площади треугольника(половина произведения основания и высоты) найдем площадь треугольника АДС:
SACD= АС*ДЕ= *10*15=75см2
Сегодня мы расширили свои знания по теме «Перпендикулярность прямых и плоскостей», познакомились с теоремой о трёх перпендикулярах, доказали ее, научились применять данную теорему при решении задач.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 18563 |
| Номер материала | 934 |