
Урок «Тэтраэдр»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».
Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.
А именно о тетраэдре.
Проводить изучение многогранников будем по плану:
1. определение тетраэдра
2. элементы тетраэдра
3. развертка тетраэдра
4. изображение на плоскости
1. построим треугольник АBC
2. точка D, не лежащая в плоскости этого треугольника
3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.
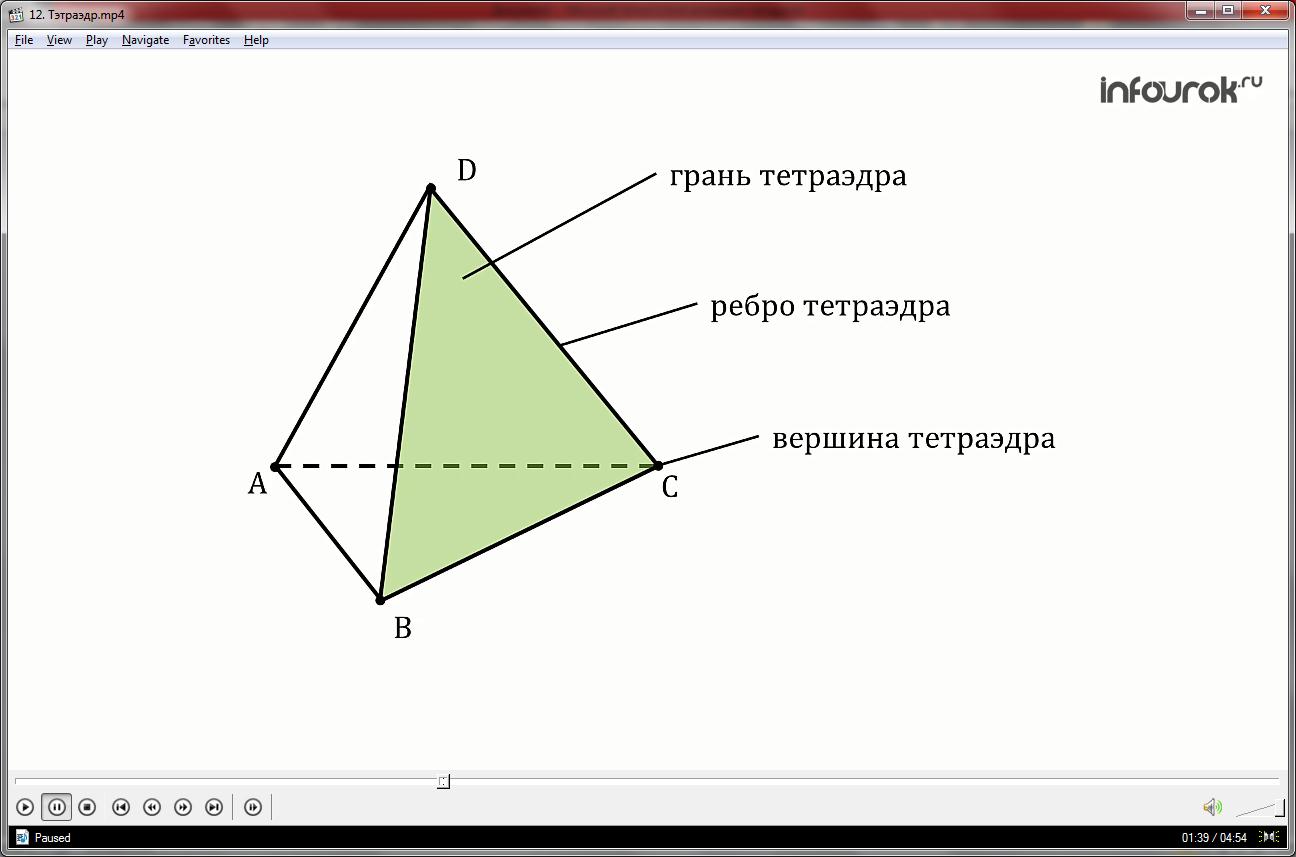
Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.
Обозначение: DABC.
Элементы тетраэдра
Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.
Сколько граней, ребер и вершин имеет тетраэдр?
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.
На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB
Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.

Развертка тетраэдра.
Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,
ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.
На плоскости тетраэдр изображается
В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.
На первом рисунке AC- невидимое ребро,
на втором – EK, LK и KF.
Решим несколько типовых задач на тетраэдр:
Задача 1.
Найти площадь развертки правильного тетраэдра с ребром 5 см.
Решение. Начертим развертку тетраэдра
(на экране появляется развертка тетраэдра )
Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.
Площадь правильного треугольника ищем по формуле:
Тогда получаем площадь тетраэдра равна:
Подставим в формулу длину ребра а=5 см,
получается
Ответ: Площадь развертки правильного тетраэдра
Задача 2
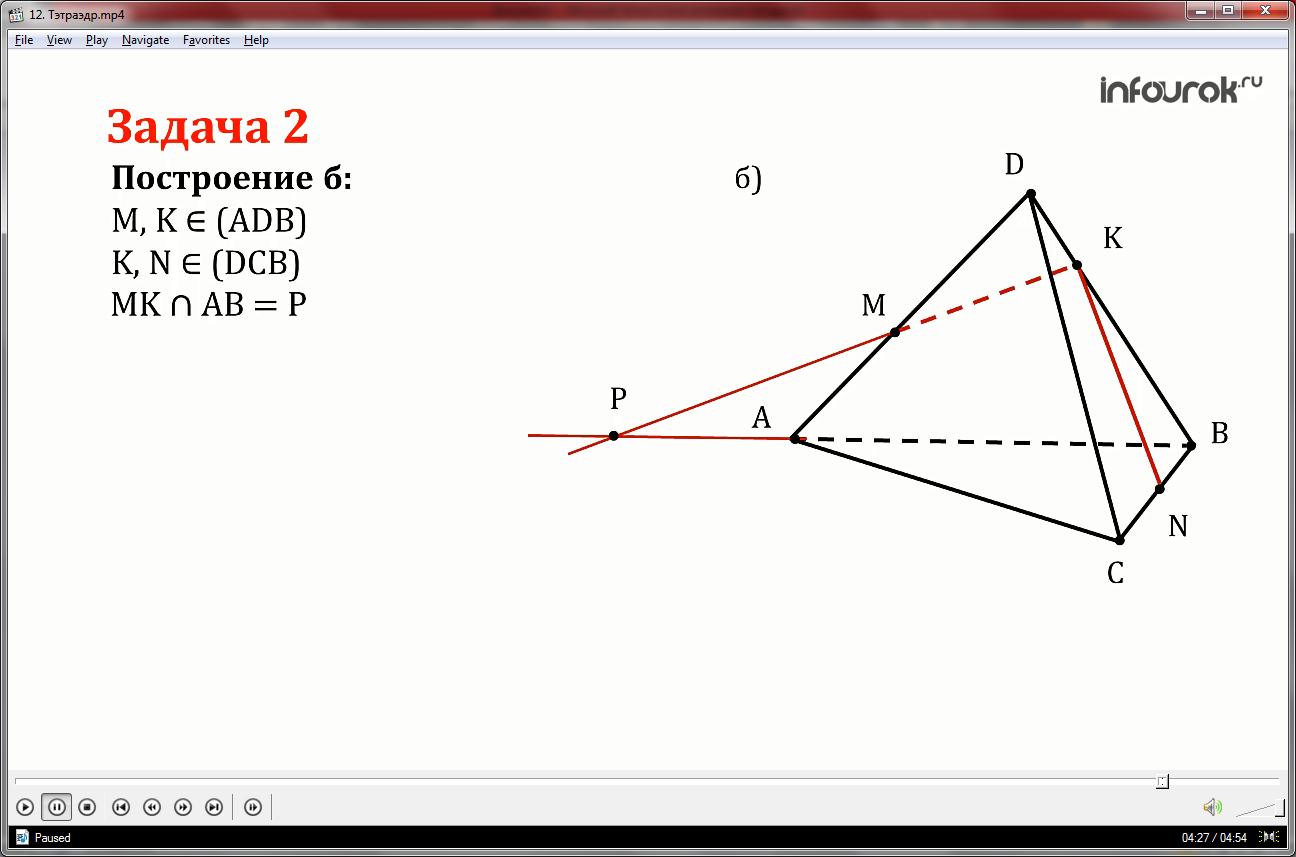
Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.
а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.
б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 12770 |
| Номер материала | 926 |