
Урок «Трёхгранный угол»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Сегодня мы познакомимся с новой геометрической фигурой - трехгранным углом.
Для изучения сегодняшней темы нам необходимо вспомнить:
1) неравенство треугольника: каждая сторона треугольника меньше суммы двух других сторон.
2) теорему о соотношении сторон и углов треугольника: напротив большей стороны лежит больший угол.
3) свойство равнобедренного треугольника:
в равнобедренном треугольнике высота, проведенная к основанию, является медианной и высотой;
3) первый признак равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу
между ними другого треугольника, то такие треугольники равны.

Определение: Трехгранный угол – это часть пространства, ограниченная тремя углами с общей вершиной, не лежащих в одной плоскости и имеющими попарно общие стороны.
Общая вершина этих углов называется вершиной трехгранного угла. Стороны углов называются ребрами, углы, заключенные между парами лучей являются плоскими углами и называются гранями трехгранного угла. Грани трехгранного угла образуют двугранные углы.
Докажет свойство плоских углов трехгранного угла:
Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов.
Доказательство
Рассмотрим трехгранный угол OEFG, предположим, что EOF EOG GOF
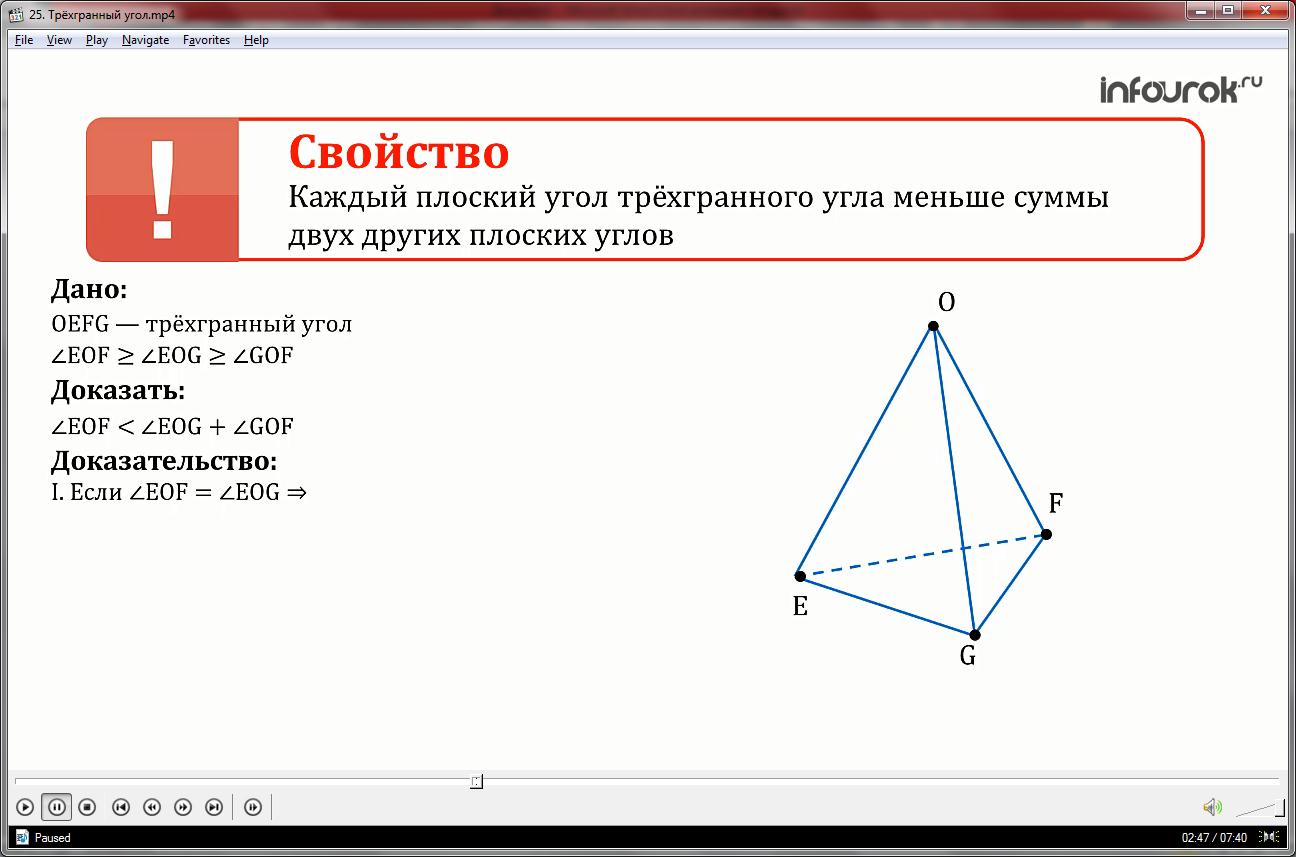
Докажем случай EOF< EOG+ GOF, остальные два доказываются аналогично.
Существуют два случая
Первый: если угол EOF равен углу EOG, то неравенство EOF< EOG+ GOF принимает вид EOF< EOF+ GOF, следовательно оно доказано.
Второй, когда EOF > EOG.
Поступим следующим образом на EF выберем точку S, где угол EOG равен углу EOS, а поскольку EOG < EOF, то точка S, находиться между точками E и F.
Следующее, что мы сделаем, построим на луче OG точку R, где OS равно OR. Тогда получаем, что треугольники EOR и EOS равны по двум сторонам и углу между ними. Из равенства треугольников получаем, что ES равно ER.
В основании получаем треугольник ERF из неравенства EF< ER+ RF, где EF= ES+SF и ES =ER, следует, что SF < RF.
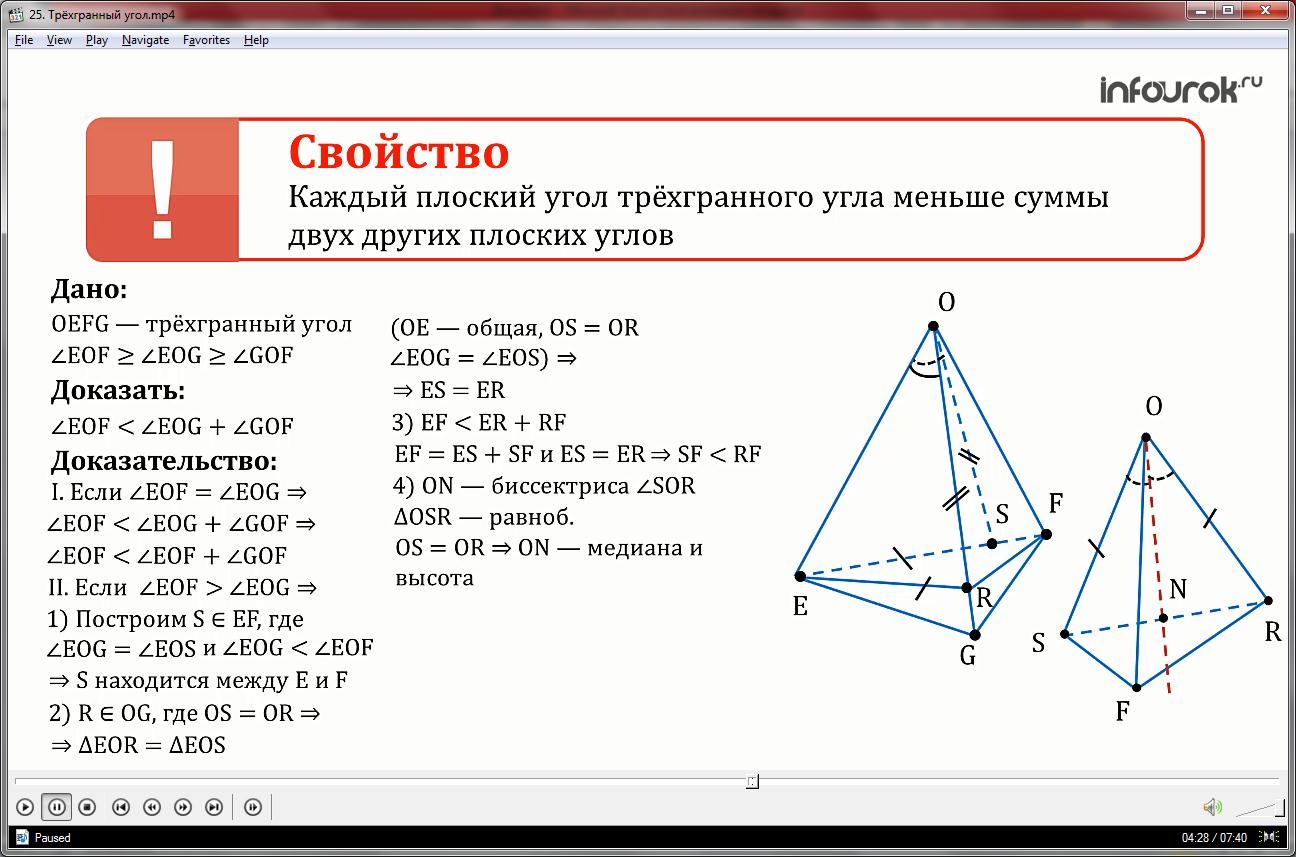
Развернем двугранный угол EOFR в одну плоскость ROFS и построим биссектрису (ON) угла SOR, равнобедренного треугольника OSR где OS равно OR (по построению), тогда получаем что биссектриса угла SOR является медианной и высотой, как биссектриса, проведенная к основанию, т.е. SN равно NR и ON перпендикулярно SR.
Из выше доказанного следует, что ON пересекает большую из сторон треугольника RDF сторону ER
Тогда получаем что угол SOF меньше угла ROF, т.к. ROF равен сумме углов RON и NOF.
Из всего доказанного, следует, что
угол EOF равен сумме углов EOS и SOF, где EOS равен EOG и все это меньше суммы углов EOR и ROF, т.е. EOG и GOF.
что и требовалось доказать.
Решим задачу
Докажите, что сумма плоских углов трёхгранного угла меньше
360º.
Решение. Пусть TMNL – трёхгранный угол с вершиной T.
Точки M, N, L принадлежат ребрам трехгранного угла.
Построим треугольник MNL, получим еще три трехгранных угла. Применим к ним свойство плоских углов трехгранного угла, получим
Неравенства при вершине M ( TML+ TMN> LMN),
при вершине L
( TLM+ TLN > MLN),
при вершине N
(TNL+ TNM > LNM).
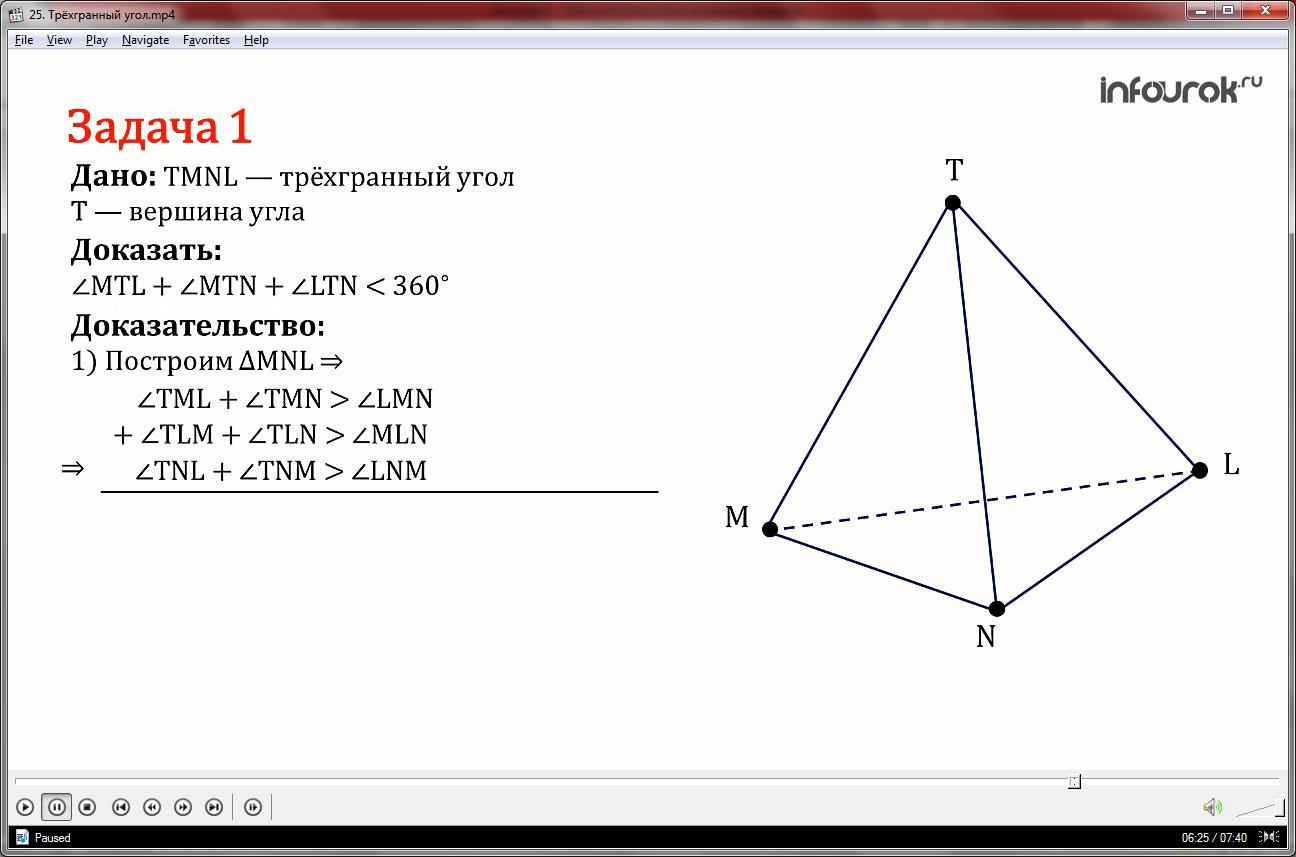
Далее мы складываем все неравенства, по частям, получаем одно неравенство, где в правой части, находятся углы треугольника MNL, а в левой сумма пар углов треугольников построенных на плоских углах трехгранного угла TMNL.
Используя свойство неравенства отнимает его обе части от положительного числа 540º, поменяв его знак на противоположный, в левой части число 540º представляем в виде суммы трех числе 180º и сгруппировав их,
Получаем неравенство, где в левой части сумма плоских углов трехгранного угла TMNL
Применив теорему о сумме углов треугольника, получаем неравенство
MТL+ MTN+ LTN<360º
что и требовалось доказать.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 17568 |
| Номер материала | 939 |