
Урок «Углы с сонаправленными сторонами»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Углы с сонаправленными сторонами.
Для изучения сегодняшней темы нам необходимо вспомнить
Признак параллелограмма: Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм
Любая прямая a, лежащая в плоскости, разделяет плоскость на две части, называемые полуплоскостями. Прямая a называется границей каждой из этих полуплоскостей.

Это одна из аксиом планиметрии.
Два луча OA и O1A1 в пространстве называются одинаково направленными (сонаправленными), если один из их содержит другой или они параллельны и лежат в одной полуплоскости с границей OO1.
Теорема. Если стороны двух углов соответственно сонаправлены, то такие углы равны.
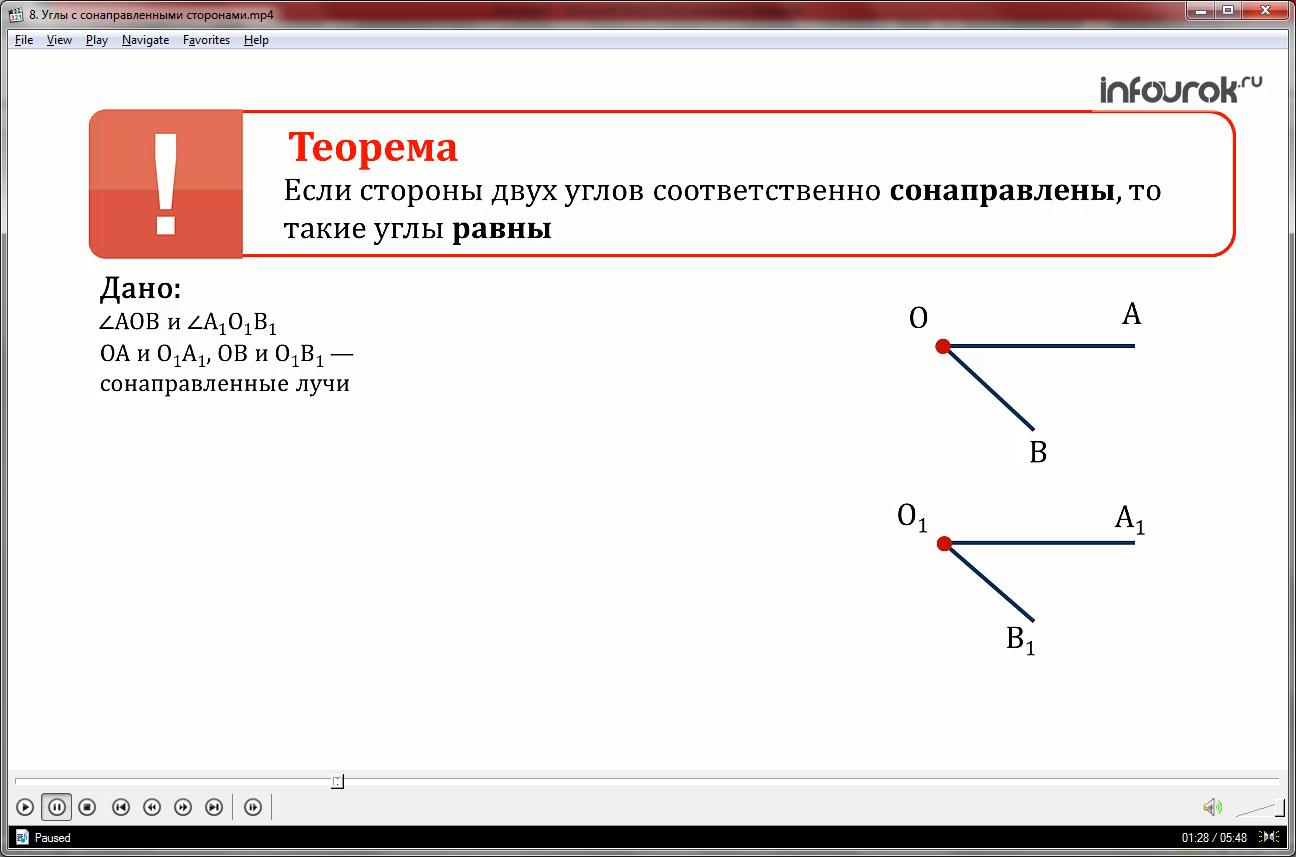
По условию теоремы нам даны углы АОВ и А1О1В1 и известно что их стороны соответственно сонаправлены т.е. ОА и О1А1, ОВ и О1В1 – сонаправленные лучи
Доказать что данные углы равны
При доказательстве ограничимся случая, когда углы лежат в разных плоскостях.
1.Стороны углов сонаправлены, а значит параллельны. Проведем через них плоскости и как показано на чертеже.
Отметим на сторонах угла O произвольные точки A и B.
На соответствующих сторонах угла O1 отложим отрезки O1A1 и O1B1 равные соответственно ОA и OB.
2. В плоскости рассмотрим четырехугольник OAA1O1.
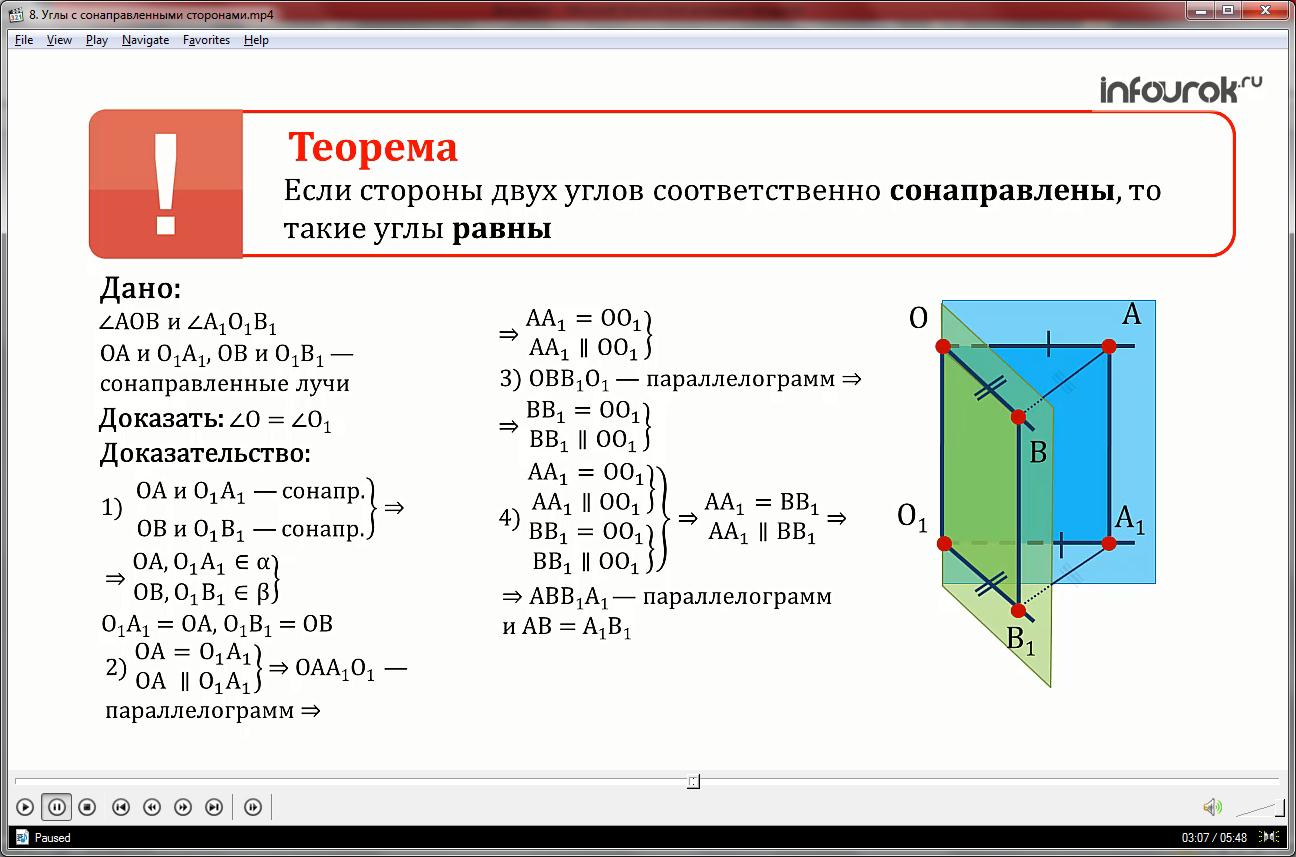
Так как противолежащие стороны OA и O1A1 этого четырехугольника равны и параллельны по условию, то этот четырехугольник – параллелограмм и, следовательно, равны и параллельны стороны AA1 и OO1
3. В плоскости , аналогично можно доказать, что OBB1O1 параллелограмм, поэтому равны и параллельны стороны ВВ1 и OO1
4. Если две отрезка AA1 и BB1 равны параллельны третьему отрезку OO1, значит они равны и параллельны, т. е. АА1||BB1 и AA1 = BB1.

По определению четырехугольник АВВ1А1 – параллелограмм и из этого получаем АВ=А1В1
5. из выше построенного и доказанного АВ=А1В1, ОA =O1A1 и OB =O1B1 следуем что треугольники AOB и A1O1B1. равны по трем сторонам, и поэтому О= О1
Теорема доказана.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 29947 |
| Номер материала | 922 |