
Урок «Угол между прямыми»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Угол между прямыми
Нами уже было рассмотрено три случая взаимного расположения прямых:
- прямые, которые имеют только одну общую точку, т.е. прямые пересекаются
- прямые не пересекаются, но лежат в одной плоскости, т.е. прямые параллельны
- прямые не лежат в одной плоскости, т.е. прямые скрещиваются
Углом между пересекающимися прямыми называют тот угол, который не превосходит любой из трех остальных углов (т.е. наименьший из четырех образованных углов).
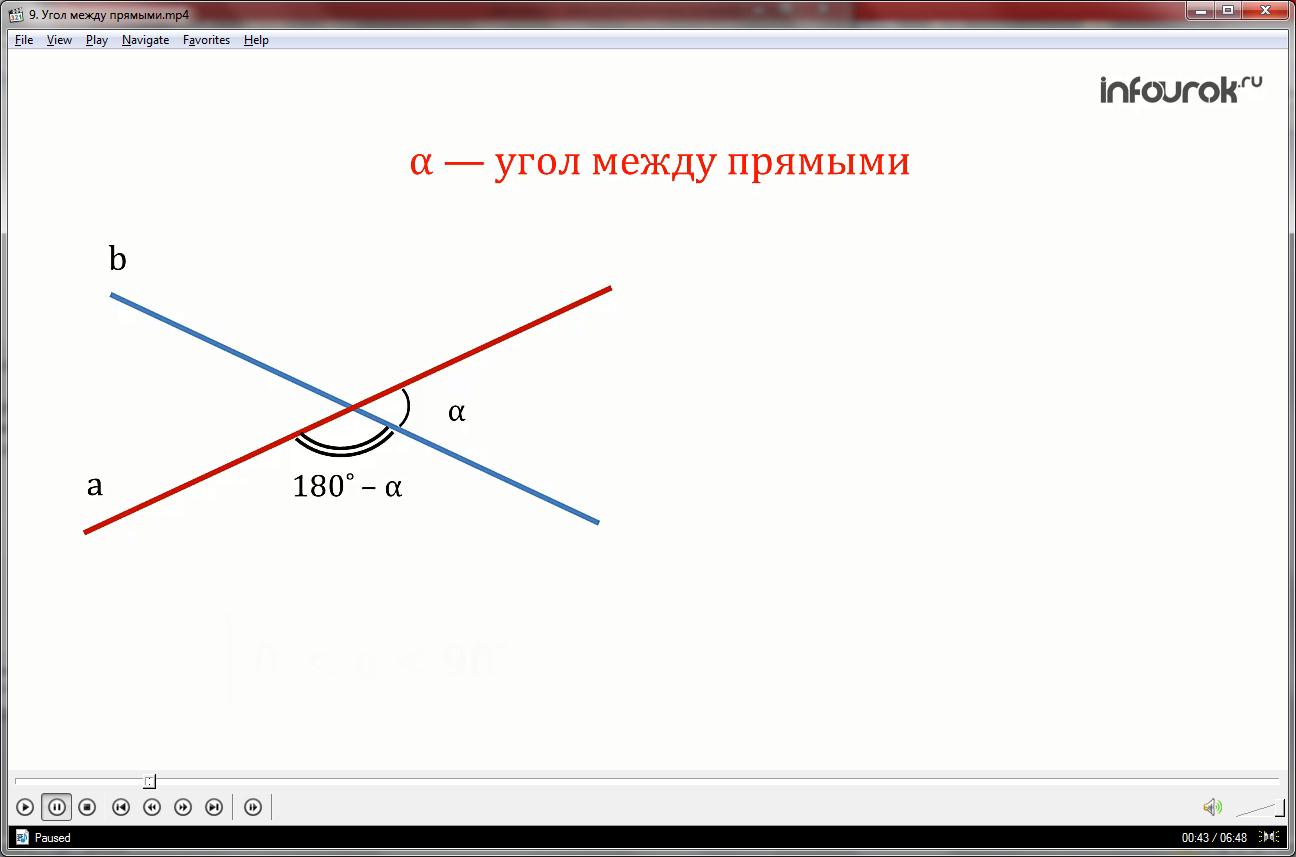
Если прямые перпендикулярны, то величина угла между пересекающимися прямыми будет равна 90˚.
Значит, угол между пересекающимися прямыми может быть острым или прямым, а величина его больше 0, но меньше или равна 90˚
Мы рассматривали углы между пересекающимися прямыми в одной плоскости. Попробуем определить угол между скрещивающимися прямыми.
Для этого мы построим прямые, параллельные данным так, чтобы они лежали в одной плоскости. (картинка)
Так для скрещивающихся прямых АВ и СD углом, является угол А₁K₁D₁, образованный пересекающимися прямыми А₁В₁ и С₁D₁ параллельные соответственно АВ и СD.

Определим, зависит ли величина А1K1D1 от выбора точки K₁.
Отметим произвольную точку K₂ и проведём через неё прямые A₂B₂ и C₂D₂ параллельные AB и CD соответственно.
На одной из прямых, например, CD возьмём некоторую точку K' и построим A´B´, содержащую данную точку.
По теореме о трёх параллельных прямых, A₁B₁ ||A₂B₂ || A'B', так как каждая из них параллельна AB.
По теореме о трёх параллельных прямых C₁D₁ || C₂D₂.
Следовательно стороны углов A'K'D, A₁K₁D₁ и A₂K₂D₂ соответственно сонаправлены.
Значит, A'K'D = A₁K₁D₁ = A₂K₂D₂ по теореме об углах с сонаправленными сторонами.
Таким образом, рассмотрев несколько построений относительно различных точек К₁, К₂, К' мы пришли к выводу, что: «Величина угла между скрещивающимися прямыми от выбора точки не зависит».
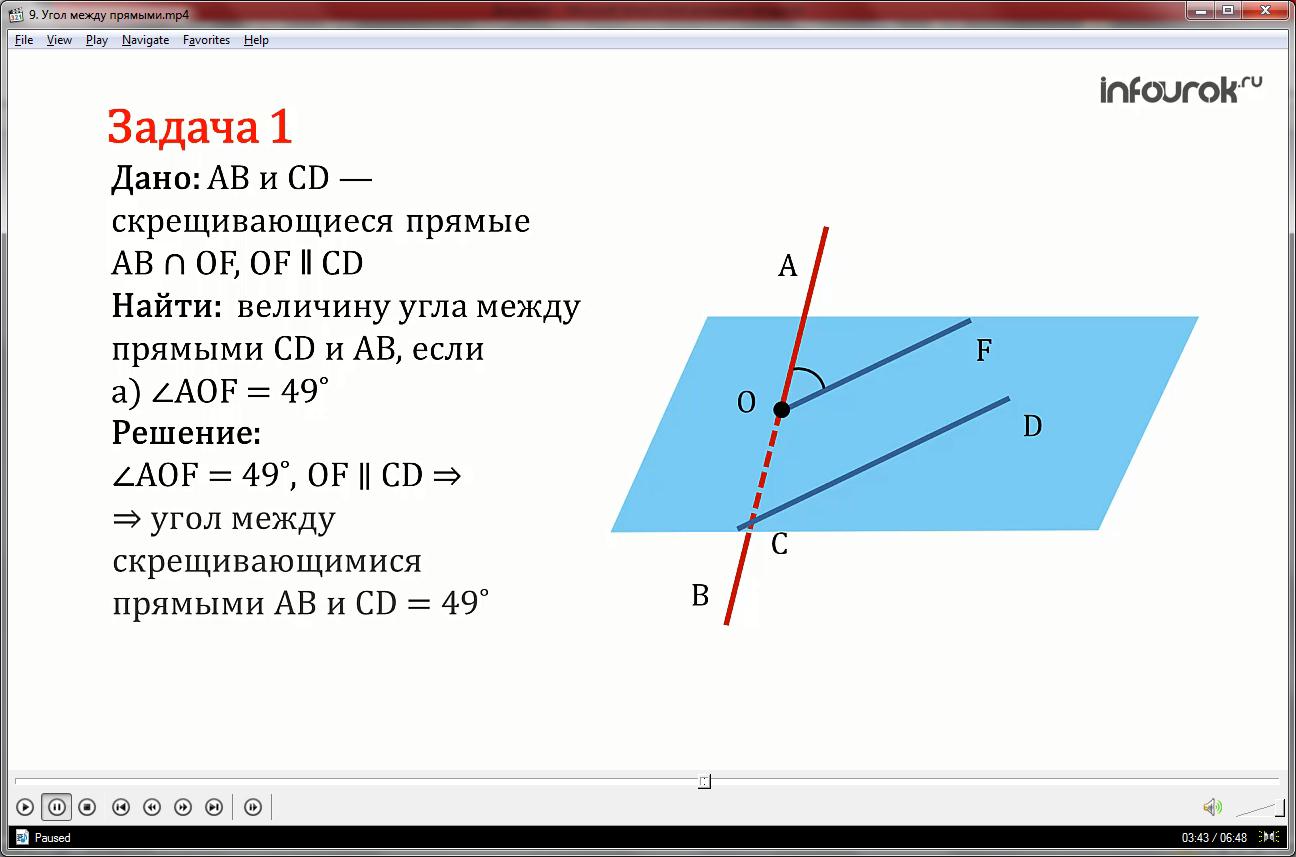
Найдем величину угла между скрещивающимися прямыми.
Перед нами АВ и CD – скрещивающиеся прямые, AB и OF – пересекающиеся, а OF и CD – параллельные.
Чему равна величина угла между прямыми СD и АВ, если:
а) AOF = 49˚
Так как AOF = 49˚ ; OF || CD, то угол между скрещивающимися прямыми АВ и СD равен 49˚.
б) Если ВOF = 104˚ , то угол между прямыми АВ и СD равен 76˚. Так как величина угла между пересекающимися прямыми OF и АВ больше 0˚, но меньше или равна 90˚, а значит равна величине AOF = 180˚ – 104˚ = 76˚ по свойству смежных углов.
Если АOF = 151˚ , то угол между прямыми АВ и СD равен 29˚.
По определению угла между прямыми он не должен превышать 90º, тогда величина угла между пересекающимися прямыми OF и АВ равна 180˚ – 151˚ = 29˚, следовательно угол между скрещивающимися прямыми АВ и СD равен 29˚.
Прямоугольный треугольник ACD с прямым углом С и равнобедренный треугольник ABC с основанием AC лежат в разных плоскостях. Точки F, K, N и M являются серединами сторон AB, BC, CD и DA соответственно. ABC = 28˚, MN = ND = 3см.
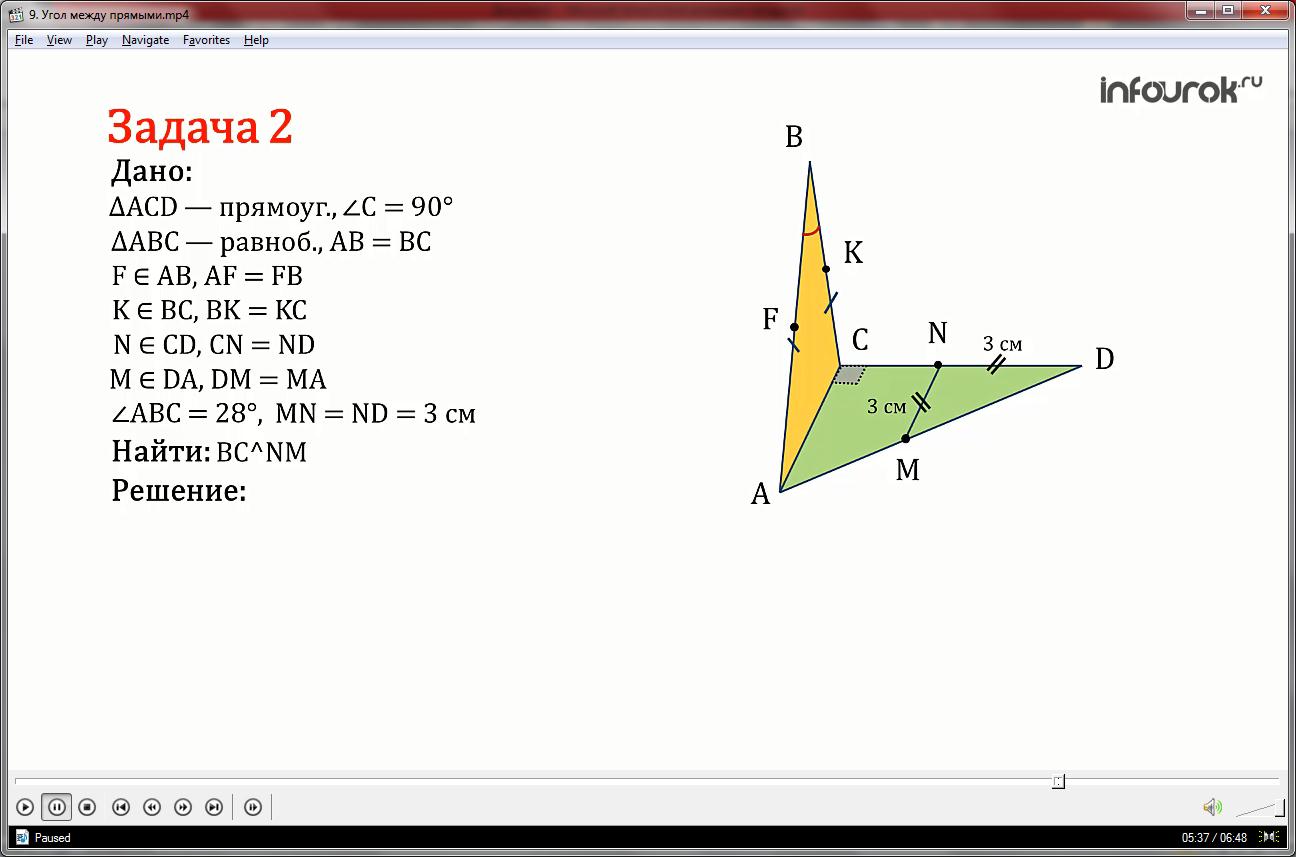
Определить угол между прямыми BC и NM, AD и FK.
Решение
Вспомним что если отрезок соединяет средины двух сторон треугольника то он является средней линией,
И то теореме о средней линии треугольника он равен половине третьей стороны и параллелен ей.
Прямые АС и MN параллельны, т.к. MN средняя линия треугольника АСD.
Тогда получаем угол между прямыми BC и NM равен углу между АС и NM и равен углу ВСА.
Найдем его
Рассмотрим треугольник АВС по условию он равнобедренный и АС его основание, отсюда имеем углы ВСА и ВАС равны как углы при основании равнобедренного треугольника,
Из теоремы о сумме углов треугольника выразим угол ВСА он равен половине разности 180 градусов и угла АВС.
Подставив значение угла АВС, находим угол ВСА равен 76 градусов
Угол между прямыми BC и MN равен 76 градусов.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 12521 |
| Номер материала | 923 |