
Урок "Умножение одночлена на многочлен"

Краткое описание документа:
В представляемом видеоуроке мы подробно рассмотрим вопрос умножения многочлена на какое-либо выражение, отвечающее определению «моном», или одночлен. Мономом может выступать любое свободное числовое значение, представленное натуральным числом (в любой степени, с любым знаком) либо же некая переменная (с подобными атрибутами). При этом стоит помнить, что многочлен представляет собой набор алгебраических элементов, называемых членами полинома. Иногда некоторые члены могут быть приведены с подобностью и сокращены. Настоятельно рекомендуется проводить процедуру приведения подобных слагаемых после операции умножения. Конечным ответом, в таком случае, будет являться стандартизованная форма полинома.
Как следует из нашего видео, процесс умножения одночлена на многочлен можно рассматривать с двух позиций: линейной алгебры и геометрии. Рассмотрим операцию умножения многочлена с каждой стороны – это способствует универсальности применения правил, особенно в случае комплексных задач.
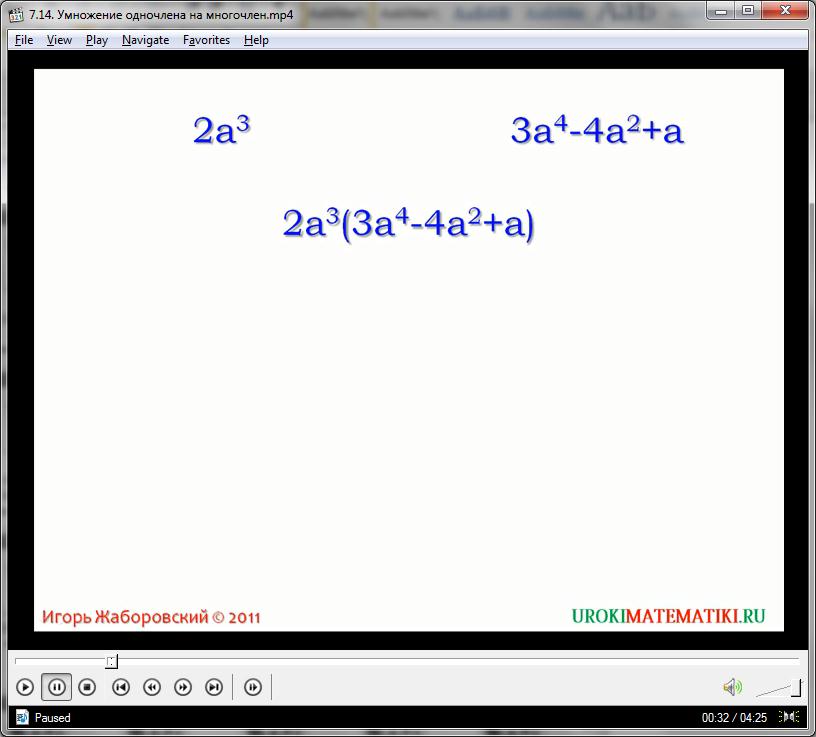
В алгебраическом понимании, умножение полинома на одночлен отвечает стандартному правилу умножения на сумму: каждый элемент суммы должен быть умножен на заданное значение, а полученное значение алгебраически сложено. Стоит понимать, что любой многочлен – это развернутая алгебраическая сумма. После умножения каждого члена полинома на некое значение мы получим новую алгебраическую сумму, которую принято приводить к стандартному виду, если это возможно, конечно.

Рассмотрим умножение многочлена в данном случае:
3а * (2а2 + 3с - 3)
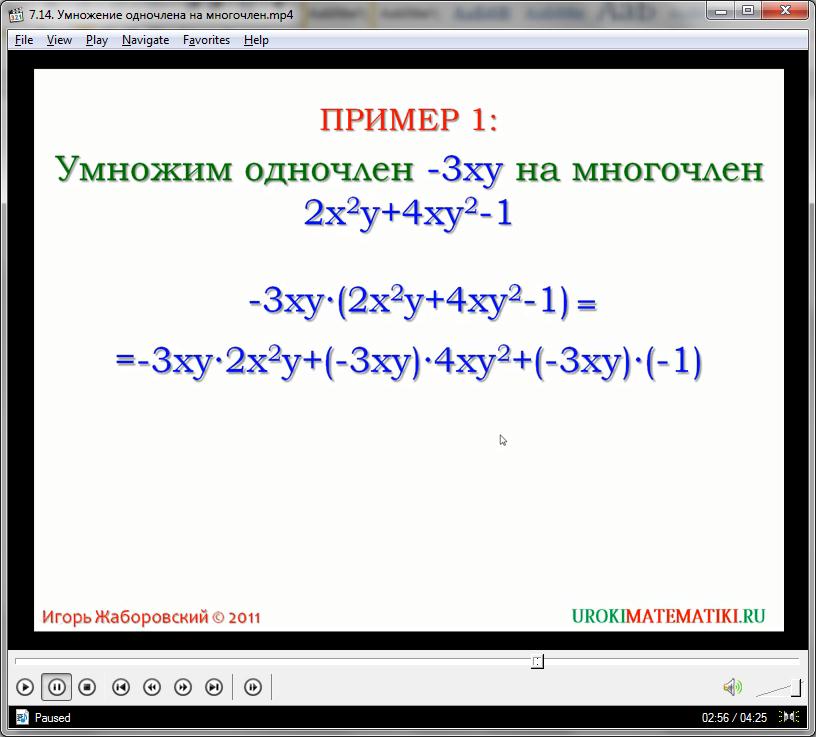
Легко понять, что тут выражение (2а2 + 3с - 3) является многочленом, а 3а – свободным множителем. Для решения этого выражения достаточно переумножить каждый из трех членов полинома на 3а:
3а*2а2 = 6а3
3а*3с=9ас
3а*(-3)=-9а
При этом стоит помнить, что знак является важным атрибутом переменной справа, и его нельзя потерять. Знак «+», как правило, не записывается, если с него начинается выражение. При умножении чисельно-буквенных выражений все коэффициенты при переменных элементарно перемножаются. Одинаковые переменные повышают степень. Разные переменные остаются неизменными, и записываются в одном элементе: а*с = ас. Знание этих простейших правил сложения способствует корректному, и быстрому решению любых подобных упражнений.
Мы получили три значения, которые являются, по сути, членами итогового многочлена, что и есть ответом на пример. Необходимо лишь алгебраически сложить данные значения:
6а3 + 9ас +(– 9а) = 6а3 + 9ас – 9а
Скобки раскрываем, сохраняя знаки, так как это алгебраическое сложение, и между мономами по определению стоит знак «плюс». Итоговый стандартный вид многочлена является корректным ответом на представляемый пример.
Геометрический вид умножения многочлена на одночлен представляет собой процесс нахождения площади прямоугольника. Предположим, у нас есть некий прямоугольник со сторонами а и с. Фигура разбита двумя отрезками на три прямоугольника различной площади, так, что сторона с является для всех общей, или одинаковой. А стороны а1, а2 и а3 в сумме дают начальную а. Как известно из аксиоматического определения площади прямоугольника, для нахождения этого параметра необходимо перемножить стороны: S = а*с. Либо же, S = (а1 + а2 + а3) * с. Проведем умножение многочлена (образованного сторонами меньших прямоугольников) на одночлен – главную сторону фигуры, и получим выражение для S: а1*с + а2*с + а3*с. Но если внимательно присмотреться, то можно заметить, что данный многочлен является суммой площадей трех меньших прямоугольников, которые и составляют начальную фигуру. Ведь для первого прямоугольника S = а1с (по аксиоме) и т.д. Алгебраически верность рассуждений при сложении многочлена подтверждается расчетами линейной алгебры. А геометрически – правилами сложения площадей в единой простейшей фигуре.
При проведении манипуляций с умножением многочлена на одночлен следует помнить, что при этом степени монома и полинома (общая) складываются – а полученное значение является степенью нового многочлена (ответа).
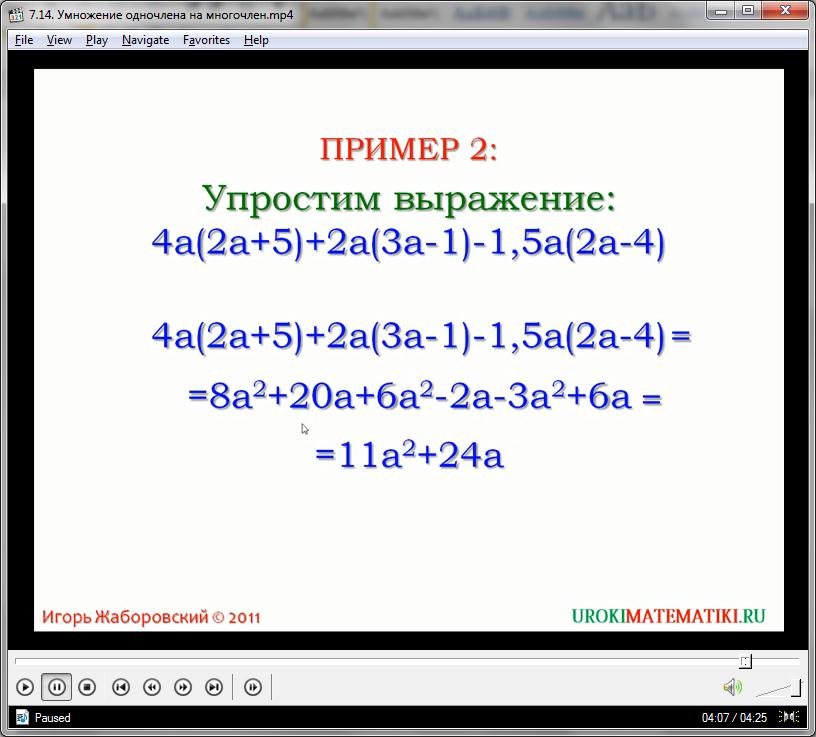
Все вышеперечисленные правила вместе с основами алгебраического сложения используются в примерах простейшего упрощения выражений, где проводится приведение подобных слагаемых и умножение элементов для упрощения всего многочлена.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5233 |
| Номер материала | 447 |