
Урок «Умножение вектора на число»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна модуль |k| умноженный на модуль |а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно.
Произведение вектора а на число k обозначается так: ka.

Для любого числа k и любого вектора а векторы а и ka коллинеарны.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение любого вектора на число нуль есть нулевой вектор.
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства:
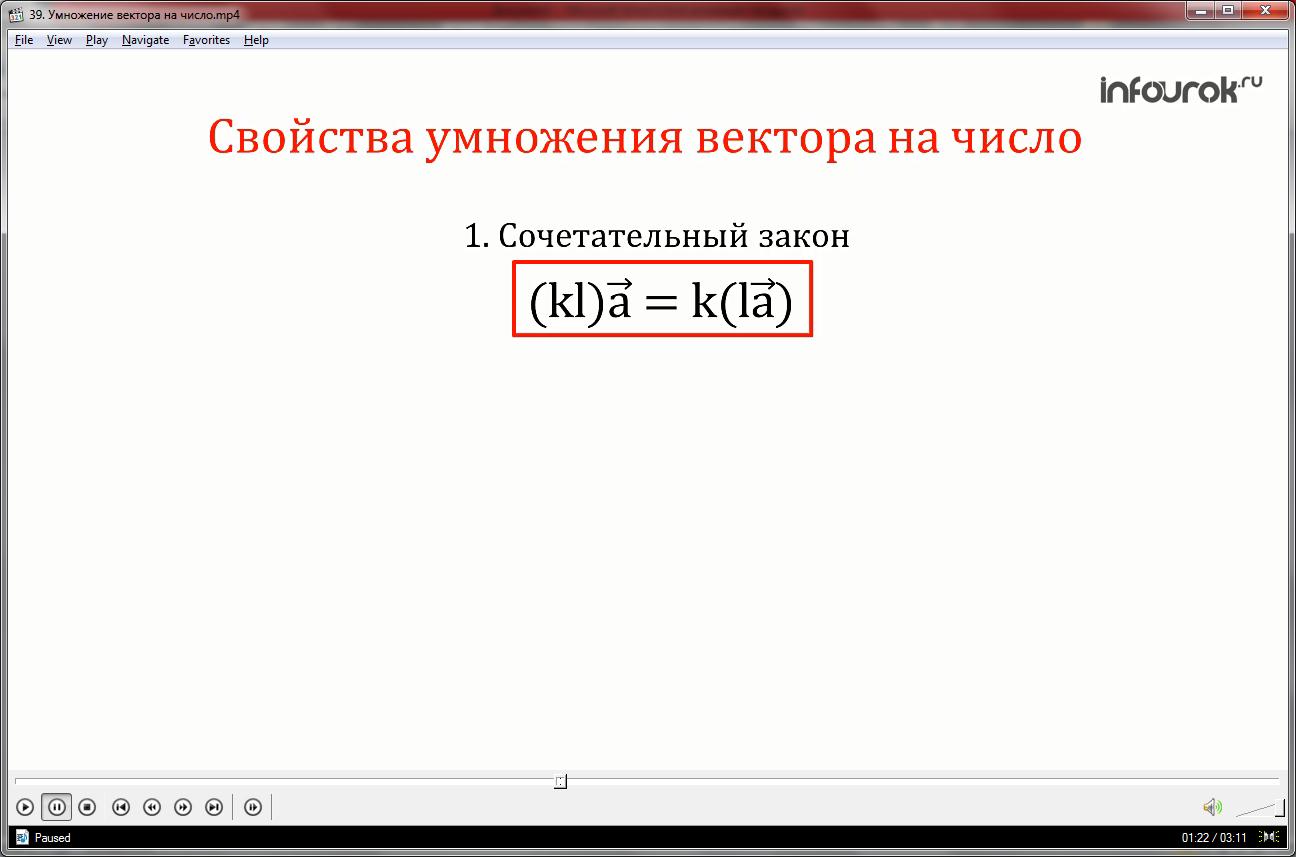
Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.
Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.
На рисунке, на примере показано это свойство.
Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.
На рисунке, на примере показано это свойство.
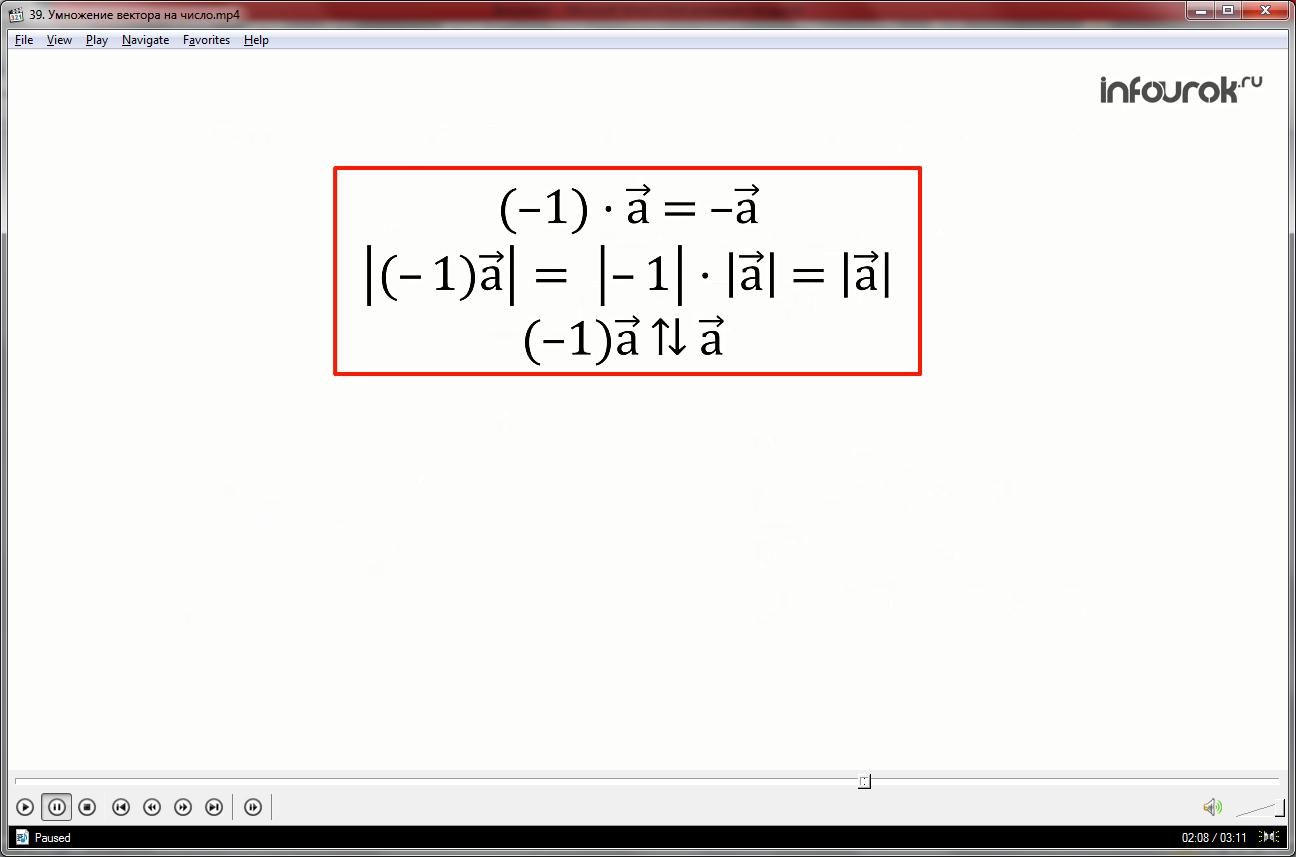
Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному.
Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие:
Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а.

Решим задачу №347 (а)
Необходимо упростить выражение.
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11107 |
| Номер материала | 953 |