
Урок «Усеченная пирамида»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем знакомство с многогранниками.
На прошлом занятии вы познакомились с частным видом пирамиды –правильной пирамидой.
Напомню, что пирамида называется правильной, если в её основании лежит правильный многоугольник. Высотой такой пирамиды называется отрезок, проведённый из вершины в центр основания.
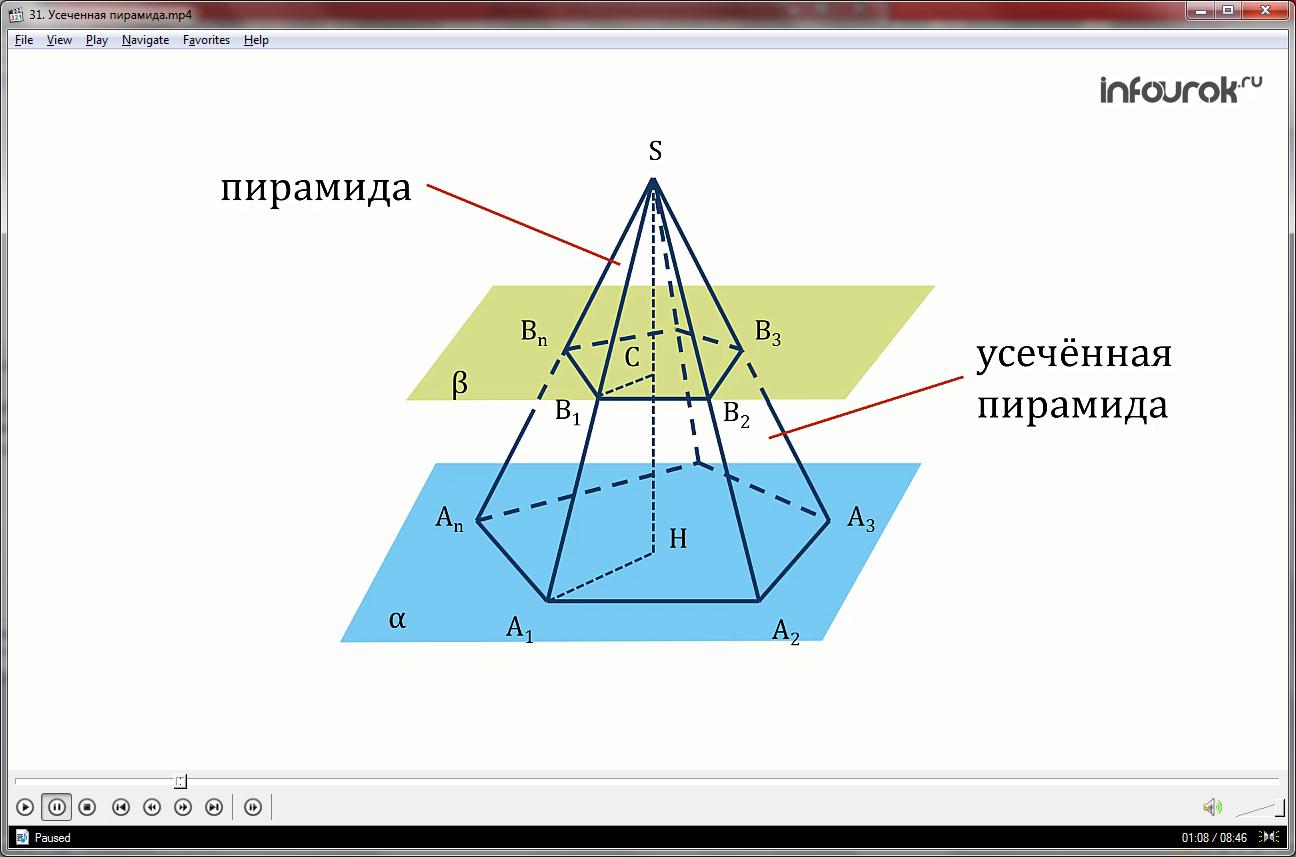
1.Изобразим произвольную пирамиду SA1 A2… An.
2. Проведём секущую плоскость параллельно основанию, пересекающую боковые рёбра пирамиды в точках В1 В2… Вn.
3.Секущая плоскость разбила пирамиду на два многогранника, один из которых так же является пирамидой., а другой называется усечённой пирамидой.
Итак, усечённой пирамидой называется многогранник, гранями которого являются многоугольники А1 А2… Аn и В1 В2… Вn(верхнее и нижнее основания), расположенных на параллельных плоскостях и четырёхугольников А1 А2 В1 В2, А2 А3 В2 В3,…Аn-1 Аn Вn-1 Вn(боковые грани).
Отрезки, соединяющие вершины оснований называются боковыми рёбрами усечённой пирамиды.
На чертеже изображена усечённая пирамида ABCDA1 B1 C1 D1.
Высотой пирамиды называется перпендикуляр, проведённый из любой точки основания к плоскости другого.
Рассмотрим боковую грань А1 А2 В1 В2 усечённой пирамиды .
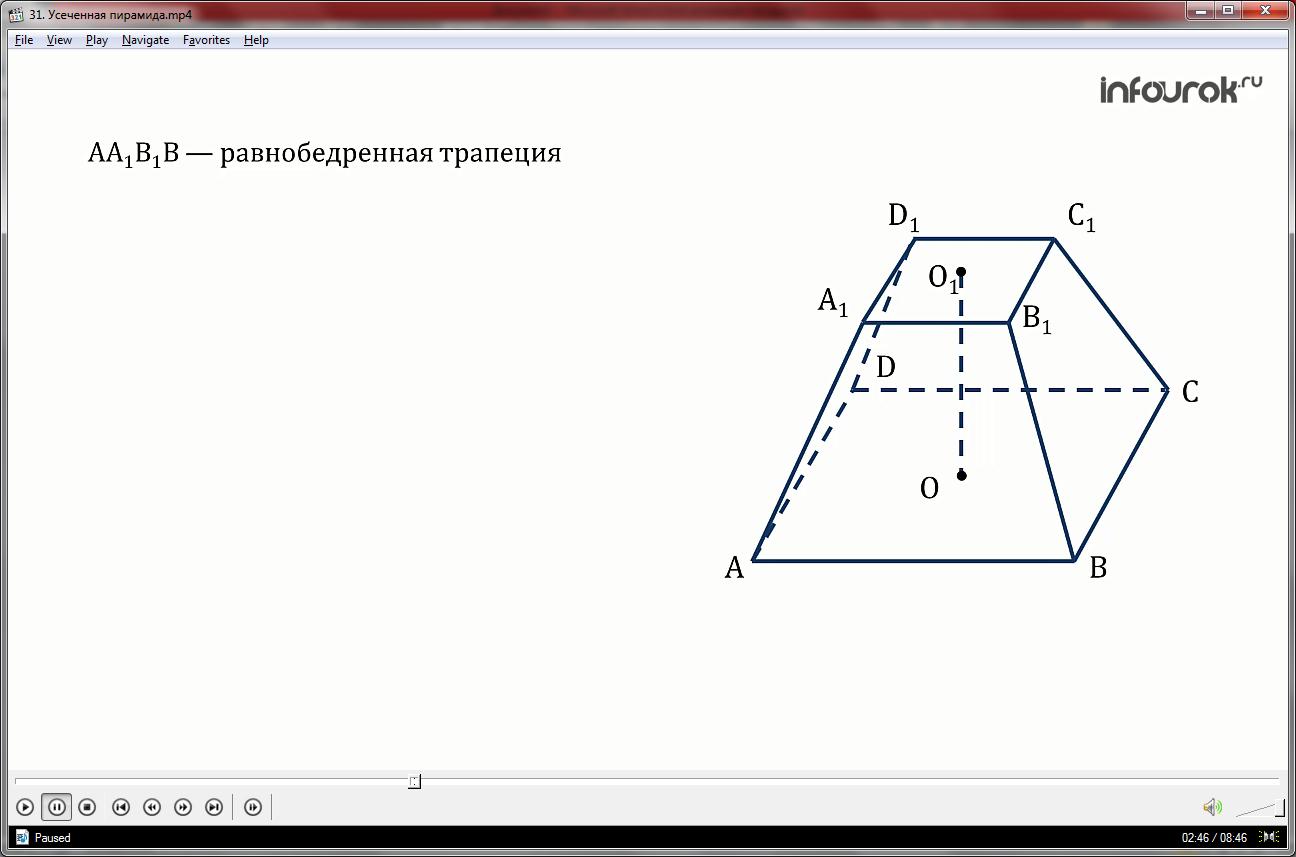
Стороны А1 А2 и В1 В2 параллельны, так как принадлежат параллельным прямым по которым плоскость S А1 А2 пересекается с параллельными плоскостями альфа и бета.
Стороны А1 В1 и А2 В2 не параллельны, так как их продолжения пересекаются в точке S.
Таким образом мы доказали, что боковая грань правильной усечённой пирамиды
А1 А2 В1 В2 -является трапецией.
Очевидно, что все боковые грани усечённой пирамиды являются трапециями.
Если усечённая пирамида получена путём сечения параллельно основанию правильной пирамиды , то усеченная пирамида будет так же правильной.
Основания правильной усечённой пирамиды –это правильные многоугольники, а боковые грани- равнобедренные трапеции.
Высота боковой грани называется апофемой.
Сумма площадей боковых граней называется площадью боковой поверхности усечённой пирамиды. Эта площадь равна произведению апофемы на полусумму периметров.
Доказательство следует из того, что боковые грани усечённой пирамиды- это равные равнобедренные трапеции, площади которых равны произведению полусуммы оснований на высоту- апофему. Вынося за скобку общий множитель –апофему и , в скобках получим сумму оснований. А это в свою очередь есть периметр оснований- правильных многоугольников.
Применим свои знания при решении задач:
Задача 1.
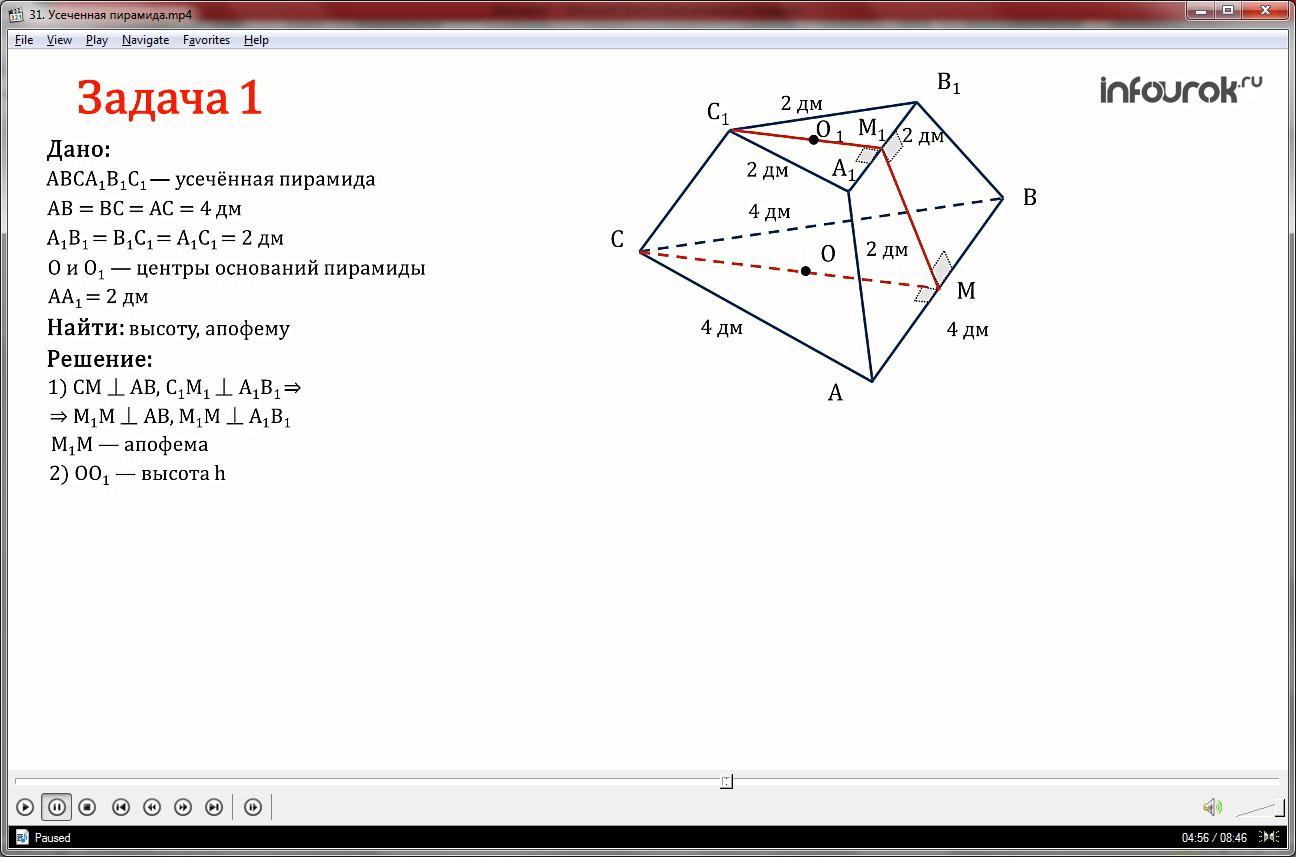
Стороны оснований правильной треугольной усечённой пирамиды равны 4 дм и 2 дм. Точки О и О1-центры оснований пирамиды. Найти высоту и апофему пирамиды, если боковое ребро равно 2 дм.
Для начала проведём краткий анализ задачи: так как усечённая пирамида правильная, то боковые рёбра-равные равнобедренные трапеции. В основании лежат правильные треугольники, значит все углы этих треугольников будут по 60 градусов.
Решение:
1. Дополнительное построение: построим СМ перпендикулярно АВ, С1М1 перпендикулярно А1В1 и соединим точки М1 и М.
По теореме о трёх перпендикулярах М1М перпендикулярен АВ(одновременно М1М перпендикулярна А1В1), значит М1М-апофема.
2. Поскольку точки О и О1-центры оснований пирамиды, то ОО1-высота h.

Дополнительное построение: построим С1L перпендикулярно СМ и М1 N так же перпендикулярно СМ.
Тогда С1L= ОО1= М1 N=h(как расстояния между параллельными прямыми).
3.Треугольники АВС и А1 В1 С1-правильные, значит ОС и О1С1-радиусы описанных окружностей треугольников АВС и А1 В1 С1.
Найдем ОС и О1С1по формуле для нахождения радиуса описанной окружности
ОС=АВ = 4 =4 дм
2sin600 2* √3
О1С1=А1В1 =2 = 2 дм
2sin600 2* √3
4.Найдем длину отрезка СL как разность между длинами отрезков ОС и О1С1:
СL= ОС- О1С1= 4 - 2 =2 дм
√3 √3 √3
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11903 |
| Номер материала | 945 |