
Презентация "Сложение и вычитание многочленов"

Краткое описание документа:
Математика в переводе с древнегреческого языка обозначает изучение, знание, наука. Эта царица наук ум в порядок приводит, помогает дисциплинировать себя и, поняв её принципы, искусно применять их в жизни. Каждому, кто соприкасается с ней она дарит ясное мышление.
Настало время ясно вспомнить изученное ранее понятие «многочлен». Ответ прост: многочлен (или полином) – это сумма одночленов.


слайды 1-2 (Тема презентации "Сложение и вычитание многочленов", пример)
Теперь нам нужно научиться выполнять простые арифметические операции с многочленами. Начнём с обычного сложения.
Например: у нас есть два многочлена: первый a^3–7a^2–1 и второй 3a^3–a^2+6
Попробуем их сложить. И по мере решения данной задачи будем формулировать правило сложения многочленов.
Итак, начнём. Каждый отдельный многочлен помещаем в скобки и между скобками ставим знак «+» вот так: (a^3–7a^2–1)+(3a^3–a^2+6)
Затем скобки раскрываем, и так как, между скобками стоит знак «+» знаки не меняем. Выглядит это так: (a^3–7a^2–1)+(3a^3-a^2+6)=a^3–7a^2–1+3a^3–a^2+6
Далее приводим подобные члены, то есть находим похожие и их складываем:
а^3+3а^3=4а^3
– 7а^2–а^2=–8а^2
–1+6 =5
Соединяем: a^3–7a^2–1+3a^3–a^2+6=4a^3–8a^2+5
У нас получился ответ: 4a^3–8a^2+5


слайды 3-4 (примеры, правила раскрытия скобок)
Подобные действия произведём с ещё одной простейшей функцией – вычитанием. Вновь предлагается взять два многочлена: первый 5b^2 – b + 1 и второй 8b^2 + 3b – 6
Опять помещаем их в скобки и между скобками ставим знак «минус»: (5b^2 – b + 1) – (8b^2 + 3b – 6)
Раскрываем скобки, меняя знаки на противоположный если перед скобкой стоял «минус», и снова приводим подобные члены:
(5b^2 – b + 1) – (8b^2 + 3b - 6) = 5b^2 – b + 1 – 8b^2 – 3b + 6 = – 3b^2 – 4b + 7
Ответ: – 3b^2 – 4b + 7
Теперь сделаем действие наоборот, а именно, научимся правильно ставить скобки после знаков «плюс» или «минус».
Возьмём, в качестве примера, следующий многочлен 5x – 3y + 1.
Задание: правильно поставить скобки после 5х и знаков «+» или «-», учитывая следующие правила:
1. Если перед скобками ставится знак «плюс», то члены, заключенные в скобки, записываются с теми же знаками. Применим «плюс».
Тогда многочлен буде выглядеть так: 5x – 3y + 1 = 5x + (– 3y + 1)
2. Если перед скобками ставится знак «минус», то у всех членов, заключенных в скобки, нужно изменить знак на противоположный.
Тот же многочлен только со знаком «минус» 5x – 3y + 1 = 5x – (3y – 1)
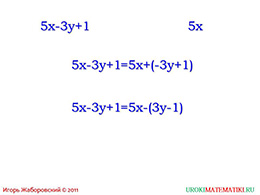
слайд 5 (пример)
Как оказалось – «всё гениальное просто».
Осталось только сделать вывод: При сложении и вычитании многочленов мы пользуемся одним и тем же принципом, поэтому надобности в различении этих операций не существует. Естественно и нет необходимости в использовании двух терминов «сложение многочленов» и «вычитание многочленов». Невероятно, две, казалось бы, разные противоположные функции являются на самом деле одним понятием «алгебраическая сумма многочленов».
Простейшие задачи с многочленом
Сегодня совершили мы, друзья.
И вывод напросился смелый:
Что братья «плюс» и «минус»
Две стороны одной медали –
Алгебраическая сумма бытия.
Это ещё раз показывает единство противоположностей, таких как, да и нет, день и ночь, покой и движение, действие и противодействие. Все это наша одно огромное понятие – жизнь!
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4001 |
| Номер материала | 186 |