
Урок "Возведение одночлена в степень"

Краткое описание документа:
Возведение любого натурального одночлена в степень сопровождается применением правил стандартного умножения. Рассмотрим такой пример:
(ах)4
Для того, что бы найти значение этого выражения, произведем почленное умножение:
(ах)4 = ах*ах*ах*ах
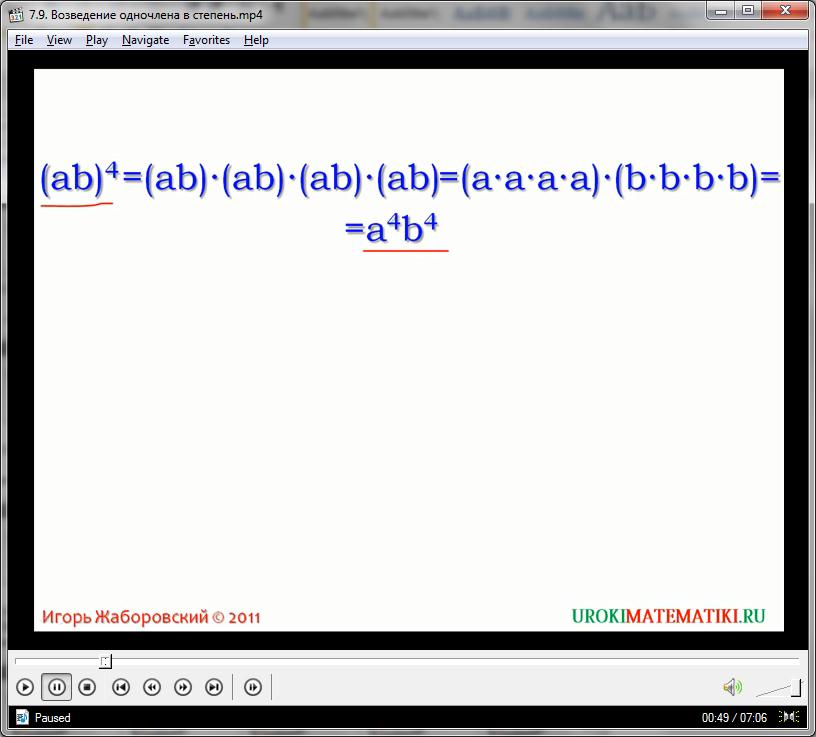
Как мы помним, любые переменные в одном одночлене являются, по факту, перемноженными. Иными словами, одночлен ах представляет собой скрытое произведение а на х. Поэтому, можно с уверенностью сказать, что:
ах*ах*ах*ах = ахахахах
С другой стороны, произведение любого количества любых одночленов дает тоже одночлен. Собственно говоря, разницы между произведением одночленов и общим мономом никакой нет. Скрытый или явный знак умножения роли особой не играет и никак не отображается на общем результате. Перегруппировав, получаем:
ахахахах = аааахххх = а4х4
Сравниваем это выражение с начальным вариантом:
(ах)4 = а4х4
Возведение в степень n одночлена, состоящего из двух переменных х и у приводит к новому одночлену, в котором и х, и у, имеют степень n:
(ху)n = (х)n(у)n
Это правило прекрасно работает для любого количества переменных в одночлене. Например, для монома асху возведение в куб будет выглядеть так:
(асху)3 = (а)3(с)3(х)3(у)3
Таким образом, что бы возвести в степень одночлен, состоящий из многих элементов, необходимо каждый из этих элементов возвести в данную степень, а результаты перемножить, так что бы получился одночлен. Основание результата будет подобным начальному моному. Не стоит забывать, что свободный член тоже является элементом одночлена и подлежит возведению в степень.
Найдем значение выражения вида:
(-3ах)3
Как мы видим, заданный одночлен состоит из трех элементов – множителей: а, х, и (-3). Каждый из них возведем в третью степень, а полученный результат перемножим, скрыв знаки умножения. При этом можно сразу рассчитать значение куба (-3):
(-3ах)3 = -27а3х3
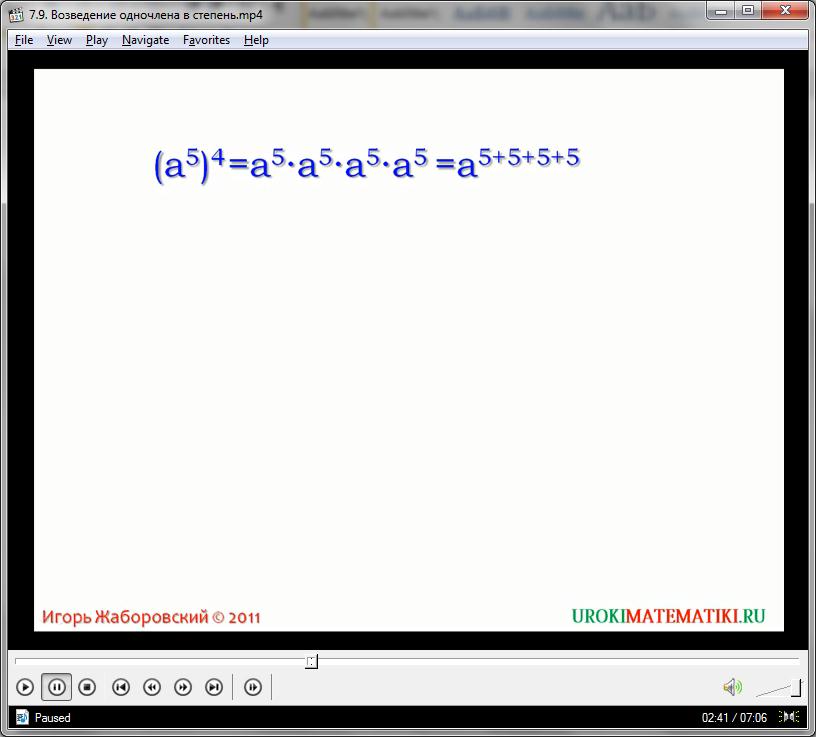
Далее в нашем видео представлена теоретическая основа для правила возведения степеней, при основаниях, уже имеющих степень, отличную от единицы. Рассчитаем почленно значение выражения:
(а4)2 = (а4)*(а4) = (аааа)(аааа) = (а)8
Мы получили одночлен, который можно сократить до основания и показателя новой степени. При возведении любого основания х, имеющего степень а, в степень у, получаем выражение вида (х)ау. Иначе говоря, в подобных случаях степени перемножаются друг на друга.
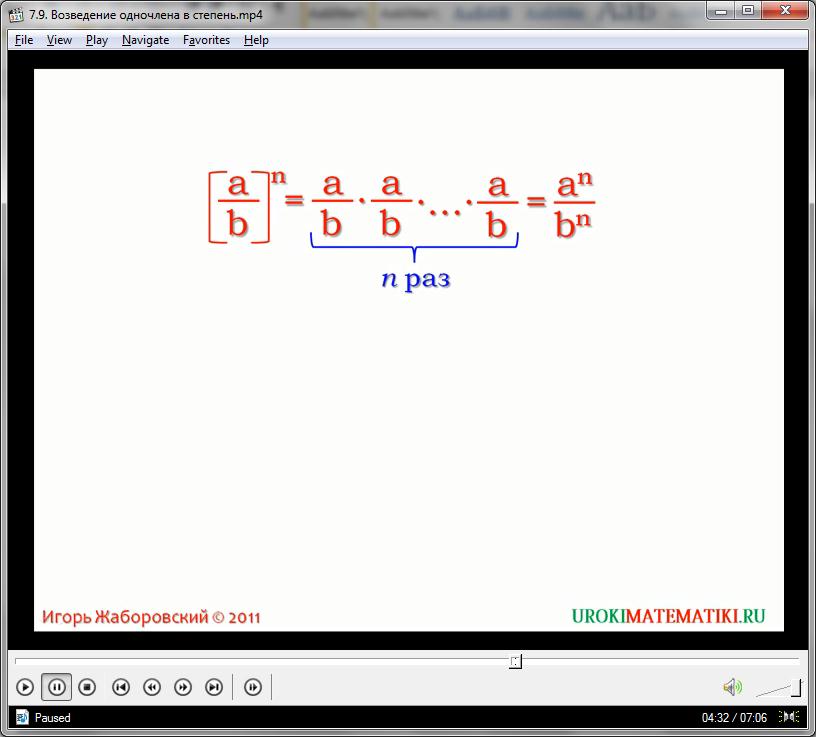
Правила деления степенных выражений имеют общие черты с правилами произведения. Действительно, произведем почленные вычисления и преобразование полученного одночлена:
(х/у)3 = (х/у)*(х/у)*(х/у) = х3/у3
При возведении в куб дроби, мы перемножили эту дробь три раза. По закону умножения дробей мы получили куб делимого и куб делителя в новой дроби. Так же, как и в случае с умножением, степень просто переносится на каждый элемент одночлена, раскрывая скобки.
Следует понимать, что операция внесения степени в скобки в случаях умножения и деления внутри одночлена всегда представляет собой процесс умножения внешней степени на каждую степень внутренних элементов. Если таковая визуально не задана – значит, она равна единице, а умножение на единицу дает начальный результат. Кроме того, следует отличать между собой выражения вида аху4, а(ху)4, (аху)4, потому что степень над скобками относится исключительно к внутреннему содержимому, никак не влияя на остальные элементы одночлена:
аху4 = аху4
а(ху)4 = ах4у4
(аху)4 = а4х4у4
Решим такое практическое упражнение. Найдем значение выражения:
(-3х3у2)6
Пользуемся вышеописанными свойствами, возводим одночлен в шестую степень:
(-3х3у2)6 = (-3)6*(х3)6*(у2)6 = 729х18у12
Все свойства умножения и деления степенных выражений работают и с основаниями, имеющими нулевую степень, при условии, что эти основания не равны нулю.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4712 |
| Номер материала | 483 |