
Презентация "Умножение многочлена на многочлен"

Краткое описание документа:
Классическая алгебра – это изучение таких выражений, которые называются полиномиальные илимногочлен. В процессе их изучения математики начали более подробно анализировать нуль, отрицательныеи комплексные числа. На основе многочлена возникла теория групп и сам процесс группировки, а прианализе начали рассматривать специальные функции.

слайды 1-2 (Тема презентации "Умножение многочлена на многочлен", пример)
«Матан» (как страшно называют студенты математический анализ) стал более быстро развиватьсяименно благодаря простоте многочлена в сравнении с другими классами отдельных функций.
Полином, или второе название многочлена, является суммой всех одночленов в выражении.
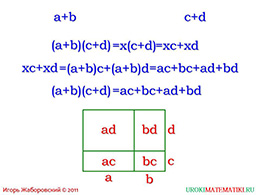
Наиболее популярная операция, которую осуществляют с таким типом выражения – умножение, поэтомунеобходимо максимально чётко понять, как умножать многочлен. Предположим, что у нас есть следующеевыражение: (a+b)(c+d)
И незнающий человек не сможет раскрыть скобки, потому что все данные разные. Однако ориентируясьв способе умножения, сразу становиться ясным, что необходимо каждый член первой части в скобкахумножить на каждый член второй части в скобках. На примере это выглядит так: (a+b)(c+d)=ac+ad+bc+bd


слайды 3-4 (правило умножения многочлена на многочлен, пример)
Количество элементов в каждой части многочлена может быть различным, однако чем их больше, темдлиннее получится решение. Что, если попробовать более сложное выражение:
(3a^2-4ab+b^2)∙(2a-b)
Непросто, но вполне осуществимо: 3a^2∙2a-4ab∙2a+b2∙2a+3a^2∙(-b)+(-4ab)∙(-b)+b^2∙(-b)
Раскроем скобки, чтобы увидеть полную картину: 6a^3-8a^2b+2ab^2-3a^2b+4ab^2-b^3
Мы видим, что есть повторяющиеся одночлены, которые можно сложить, то есть упростить выражение:6a^3-11a^2b+6ab^2-b^3

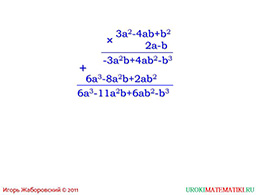
слайды 5-6 (пример)
Теперь для закрепления стоит взять ещё один пример: представим в виде многочлена произведение из2x^2-3x+1 и 5x+4
(2x^2-3x+1)∙(5x+4)=10x^3+8x^2-15x^2-12x+5x+4=10x^3-7x^2-7x+4
Работа с многочленами особенно важная, когда можно что-то упростить, чтобы сделать пример легче.Например, для начала выражение (3x-4)(2x+1)-(x-2)(6x+3) может показать сложным, но мы уже знаемособенности умножения многочлена и упростим всё следующим образом: (3x-4)(2x+1)-(x-2)(6x+3)=(6x^2-8x+3x-4)-(6x^2+3x-12x-6)=6x^2-8x+3x-4-6x^2-3x+12x+6=4x+2
Выходит что из сложного (3x-4)(2x+1)-(x-2)(6x+3) в ответе мы получаем 4x+2. Теперь сложно несогласиться с утверждением того, что данное действие упрощает сложные примеры.


слайд 7-8 (примеры)
В сборнике задач, вы можете видеть примеры следующего формата: Докажем, что при любых n значениевыражения (n+8)(n-4)-(n+2)(n-16) делится на 18.
Изначально у нас выражение (n+8)(n-4)-(n+2)(n-16), в котором необходимо раскрыть скобки иперемножить все одночлены: n^2+8n-4n-32-n^2-2n+16n+32
Мы видим, что n^2 сокращается, впрочем, как и 32, в итоге мы имеем 18n. Именно поэтому выражение(n+8)(n-4)-(n+2)(n-16) всегда будет делиться на 18. Можно также вводить дополнительные переменные.
Например: Докажем тождество (a^3+b^3+c^3+8abc)(a^3+b^3+c^3-7abc)-(a^3+b^3+c^3)(a^3+b^3+c^3+abc)=-56a^2b^2c^2
x=a^3+b^3+c^3, y=abc
(x+8y)(x-7y)-x(x+y)=x^2+8xy-7xy-56y^2-x^2-xy=-56y^2-56y^2=-56a^2b^2c^2


слайды 9-10 (примеры)
Удобство работы с многочленами состоит в том, чтобы увидеть, какие части выражения мы можемсократить. Поэтому над сложными примерами необходимо провести ряд операций, ведь всегда можетпоявиться возможность умножить многочлен.
В ещё одной науке, алгебраической геометрии, многочлен играет далеко не последнюю роль, ведь здесьобъектом выступают множества, которые являются решением система многочленов. Стоит отметить, чтомногие разделы математики опираются на работу с многочленами. В большинстве случаев длякодирования, а также для того, чтобы выразить свойства отдельных объектов с помощью многочлена.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4797 |
| Номер материала | 188 |