
Презентация "Уравнения и его корни"

Краткое описание документа:
Темой сегодняшнего нашего разговора является «Уравнение и его корни». Давайте перед тем, какприступить к ее изучению выясним, что такое корни уравнения. Корнем математического уравненияназывается его решение.


слайды 1-2 (Тема презентации "Уравнения и его корни", пример)
Такие уравнения могут принимать различный вид, например, выглядит как классическое линейноеуравнение, уравнение с многочленами и прочие.
Для того, чтобы решать подобные уравнение Вам, прежде всего, нужно будет обозначить областьопределения уравнений. Область определения уравнения часто называют еще и областью допустимыхзначений переменной в уравнении, под этим подразумевается множество значений переменной, когда обечасти уравнения существуют – имеют математический смысл.

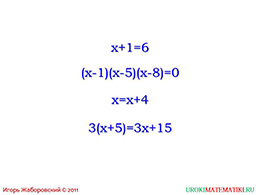
слайды 3-4 (определения, пример)
Равносильным заданное уравнение будет только при таких условиях:
1. При условии переноса слагаемого из одной части уравнения в другую, но обязательно сменив приэтом знак (это правило является одним из самых важных, поскольку многие забывают сменить знак и впроцессе решения примера у них получается неправильный ответ с правильным ходом решения).
- При условии умножения или деления обеих частей уравнения на одно и то же число, но это ни в коемслучае не может быть 0 (не забываем также, что на ноль делить нельзя).
3. При условии что, в какой-либо части уравнения, или обеих частях, выполнить тождественноепреобразование, которое бы не меняло область определения уравнения.
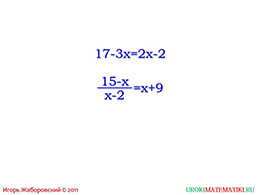

слайды 5-6 (пример, определение области определения)
При выполнении уравнений с любым количеством корней, необходимо знать все правила. В противномслучае, уравнение будет решено некорректно, и вы определите неправильное количество корней и ихзначение.
Когда вы решаете дробные уравнения нужно делать это согласно алгоритму.


слайд 7-8 (пример, получение равносильного уравнения)
Решая уравнения, содержащие дроби, является необходимым определение области допустимых значенийнеизвестного Вам знаменателя, исключив возможность равенства знаменателя нулю.
Визуально представляя такое уравнение, вы всегда должны стремиться к упрощению уравнения. Также,необходимо избавляться от знаменателя. Для этого нужно найти общий множитель к каждому изчислителей дробей, из которых состоит уравнение. После того, как знаменатель сводится, необходимоумножить все числительные на соответствующие множители. Затем, делим уравнения на правую и левуючасть посредством переноса составляющих уравнения. После этого сокращаем составляющие дополучения равенства.
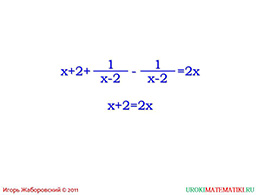

слайды 9-10 (примеры)
Как видите, решение подобных уравнений – несложная задача, которая требует лишь знание правил, атакже небольших математических навыков, и нахождение корней уравнения станет для вас настоящейзабавой.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3931 |
| Номер материала | 189 |