
Урок "Умножение многочлена на многочлен"

Краткое описание документа:
Умножение многочленов – это математическая операция, которая используется во многих задачах как тематического характера, так и комплексного. Рассмотрим основные правила и нюансы умножения многочлена на многочлен.
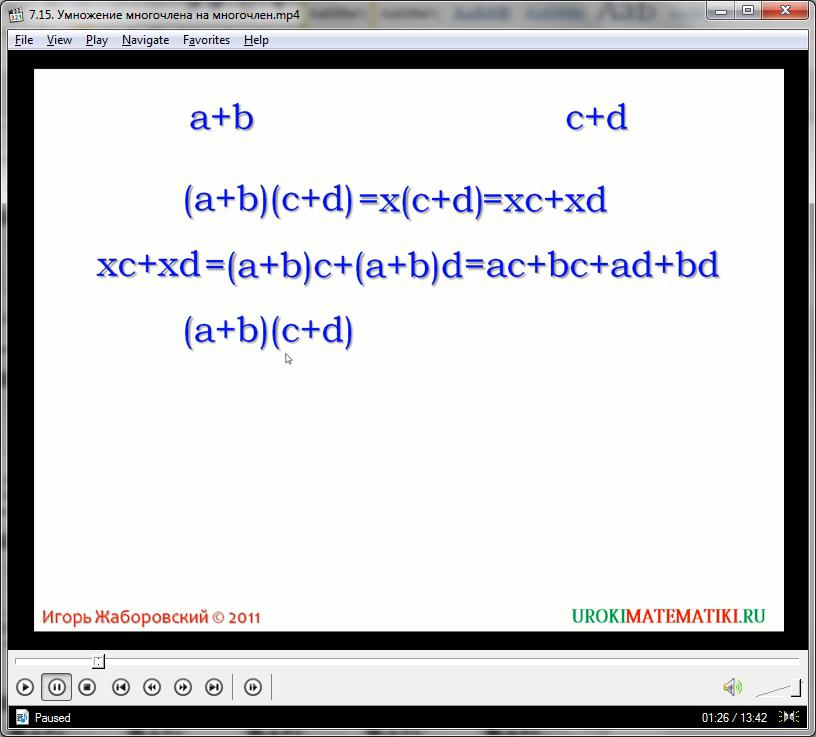
С точки зрения алгебры, умножение двух сумм (которыми являются любые полиномы) осуществляется посредством взаимного перемножения каждого из членов полинома. Это вытекает из правил умножения на одночлен. Возьмем, к примеру, выражение:
(4а +7с)*(4х – 3у)
Для решения используем подстановку новой переменной k, которая равна
(4х – 3у):
(4а +7с)*k = 4ak + 7ck
Используя стандартные правила умножения полинома на одночлен, получаем новый многочлен, который можно преобразовать (учитывая значение переменной k) к виду:
k= (4х – 3у)
4ak + 7ck = 4a(4х – 3у) + 7c(4х – 3у) = 16 ах – 12ау +28сх -21 су
Раскрывая скобки и перемножая полученные значения, приводим многочлен к стандартному виду, что и является правильным ответом на заданное упражнение. Как видим, результат полностью соответствует правилу взаимного перемножения каждого монома. Для того чтобы не запутаться, рекомендуется проводить ступенчатое перемножение с введением временной переменной, чтобы не упустить какой-либо элемент. Это особенно актуально для многочленов с большим количеством элементов. Для самопроверки существует правило: количество членов итогового многочлена (который является произведением двух полиномов) равно произведению количества одночленов в первом, и во втором многочлене. Поэтому, пересчитав мономы и перемножив их, можно получить быстрый ответ количества членов многочлена-ответа.
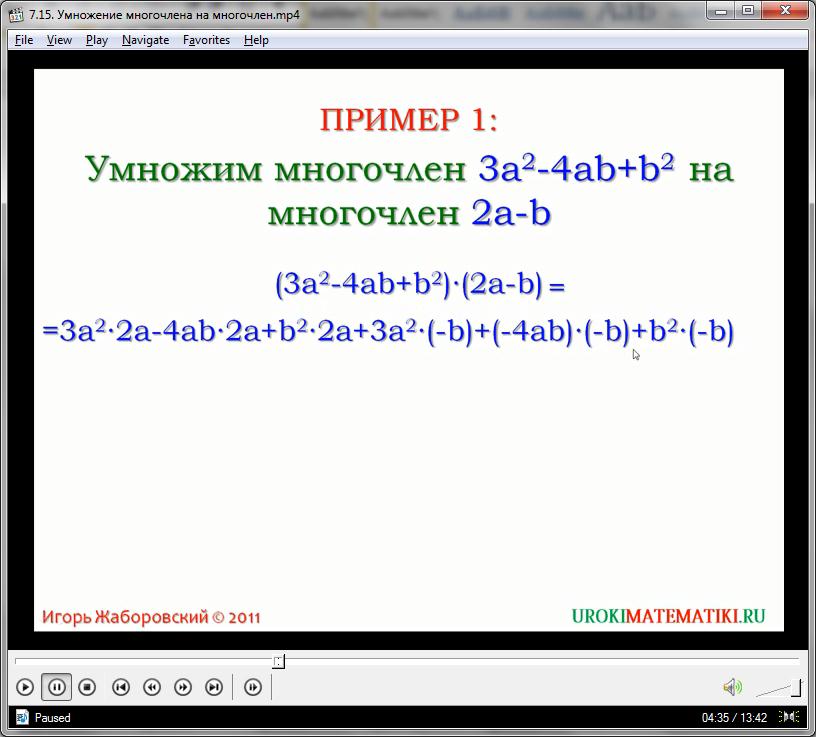
В геометрии умножение многочлена на многочлен рассматривается с точки зрения площадей прямоугольника. Для нахождения площади необходимо перемножить обе стороны фигуры. Если стороны будут представлять собой набор отрезков, являющихся, в свою очередь, сторонами более мелких вставных прямоугольников, то формула нахождения площади преобразуется в многочлен. Если отрезками будет поделена каждая сторона фигуры – то формула площади будет произведением многочленов. Однако итоговая площадь остается всегда прежней, каким бы способом её не находили, что логично подтверждает алгебраические расчеты.
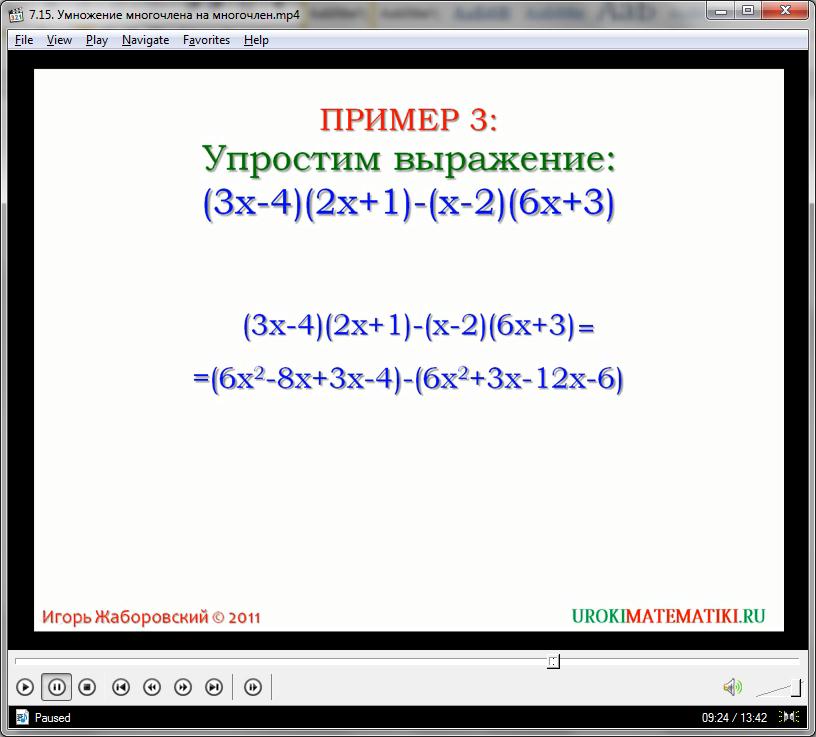
Как известно из предыдущих уроков, каждый многочлен имеет свободное числовое значение (свободный член, который может быть равен нулю, если не задан открыто), а также старший коэффициент – число при переменной, имеющей наибольшую степень.
При умножении многочленов, старшие коэффициенты перемножаются (как элементы одночленов) – а итоговое произведение является старшим коэффициентом в ответе. Свободные члены также перемножаются, образуя свободный член многочлена-ответа. При этом общие степени полиномов складываются.
Применение правил умножения многочленов часто используется в различных нетривиальных задачах. Например, необходимо доказать, что выражение вида:
(3а – а)*(7а + 4а)
делится на 22 без остатка. Проведем умножение полиномов:
(3а – а)*(7а + 4а)
21а + 12а2 – 7а2 – 4а2 = 22а2
22а2 легко поделится на 22,или любое число, кратное 22, причем без остатка, оставляя переменную в квадрате.
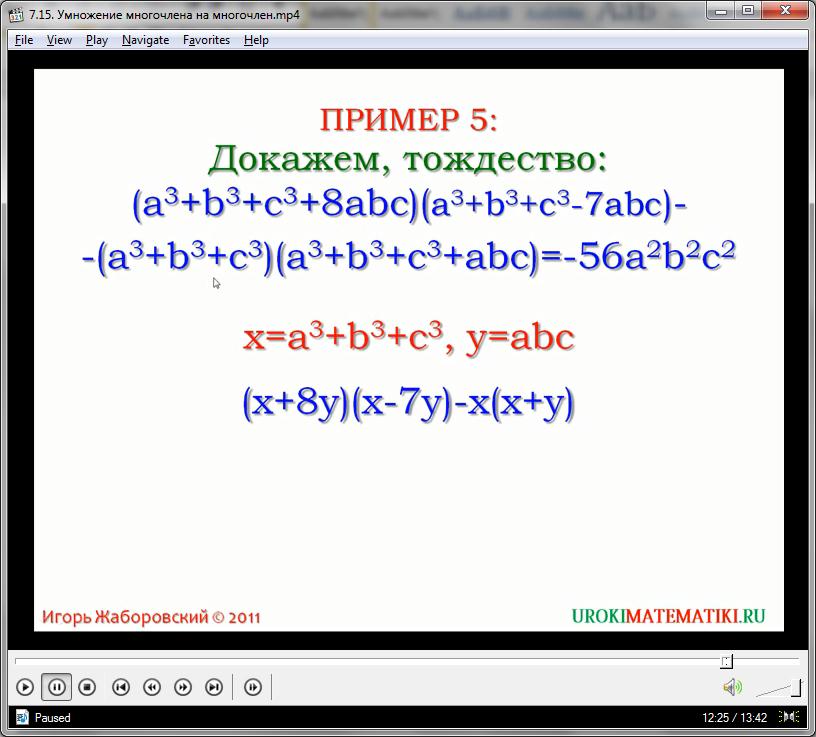
Метод введения мнимых переменных, когда известные выражения задаются, как буквенные значения, часто позволяет упростить задачу, облегчив объемный многочлен. Докажем тождество:
(7ас3 + 6а5 + 2ас3 – а5) = (5а5 +9ас3)
Для облегчения задачи представим, что х = ас3, у = а5. Т.е. выбираем подобные слагаемые или элементы с общей основой, которые можно описать одной переменной. Получаем следующее выражение:
7х + 6у + 2х – у = 5у + 9х
9х + 5у = 5у + 9х
Что и требовалось доказать. Метод подстановки в многочленах часто используется там, где не нужно искать конечное выражение, а необходимо что либо доказать.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5239 |
| Номер материала | 448 |