
Презентация "Перпендикуляр к прямой"

Краткое описание документа:
В данному уроке мы подробно рассмотрим понятие перпендикуляра к прямой и докажем важную теорему.
Прямая – это бесконечное количество точек, расположенных на одной линии. Отрезок – это участок прямой, ограниченный двумя точками, состоящий из всех точек, расположенных между граничными точками, и этих двух граничных точек. Прямые являются одним из основополагающих понятий евклидовой геометрии.


слайды 1-2 (Тема презентации "Перпендикуляр к прямой", определение перпендикуляра)
Перпендикуляр – это отрезок или прямая, расположенная под углом девяносто градусов по отношению к другой прямой. Если перпендикуляром является прямая, то она образует четыре прямых угла с другой прямой, и пересекает её. В случае с отрезком, отрезок может пересекать прямую или касаться её. Если отрезок пересекает прямую, то образуются четыре прямых угла, если касается – то только два. Следовательно, перпендикуляром также можно назвать прямую или отрезок, если таковые образуют с другой прямой два или четыре угла по девяносто градусов. Также, если один из углов прямой, то остальные три или один угла тоже будут прямыми.
слайд 3 (теорема)
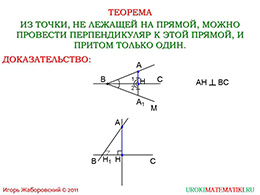
Рассмотрим теорему существования перпендикуляра к прямой. Теорема утверждает, что из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой. Дополнение к теореме – такой перпендикуляр можно провести только один.
Представим себе прямую, а на ней отрезок BC. Представим также точку A, не принадлежащую отрезку BC на прямой. Отложим луч BA, образующий угол ABC. Далее, отложим луч BM таким образом, чтобы образующийся угол MBC был равен углу ABC. Так как ABC = MBC, то мы можем наложить угол ABC на угол MBC таким образом, чтобы стороны BA и BC совместились со сторонами BM и BC. После совмещения точка A наложится на некую точку A1 луча BM. Образующаяся точка H будет точкой пересечения отрезков AA1 и BC. Также, эти два отрезка образуют смежные углы 1 и 2. При наложении лучи HA и HA1 совмещаются, а угол 1 равен углу 2. Так как углы 1 и 2 смежные и равные, то оба они прямые. Следовательно, из точки на плоскости можно провести перпендикуляр к прямой.
Единственность перпендикуляра к прямой из точки A можно доказать от противного. Предположим, что из точки A проведены два перпендикуляра к прямой. Это не является возможным, поскольку из разных точек прямой нельзя провести два перпендикуляра, имеющих одну общую точку A. Получаем противоречие. Следовательно, теорема о том что из одной точки можно провести два перпендикуляра к прямой, неверна.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7609 |
| Номер материала | 241 |