
Презентация "Третий признак равенства треугольников"

Краткое описание документа:
В данном уроке мы обсудим последний признак равенства произвольных треугольников, докажем теорему и поймём, как использовать этот признак в типовых задачах. На данный момент мы уже знакомы с первым и вторым признаком. Кто может их сформулировать?

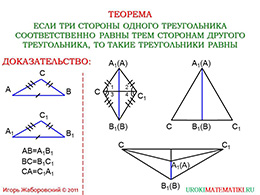
слайды 1-2 (Тема презентации "Третий признак равенства треугольников", теорема)
Третий признак треугольников доказывает их равенство через равенство всех сторон. Обратим внимание на формулировку на доске и докажем данную теорему.
Нам дано, что стороны «АВ» и «А1В1», «ВС» и «В1С1», «АС» и «А1С1» идентичны по размерам. Для того, чтобы доказать равенство треугольников «АВС» и «А1В1С1» необходимо приложить эти треугольники, чтобы сторона «АВ» и «А1В1» объединились.
Вершины «С» и «С1» расположим по разные стороны.
Рассмотрим первый случай: луч «СС1» находится внутри угла «А1С1В1», а значит и внутри угла «АСВ». Воспользуемся тем, что «АС» и «А1С1» равны между собой. Получаем равнобедренный треугольник, углы при основании будут идентичными. Значит угол один равен углу два. Аналогично рассмотрим треугольник «СВС1» и поймём, что углы при основании также идентичны (углы три и четыре равны между собой).
В итоге угол «АСВ» равняется углу «А1С1В1», из чего следует, что треугольники равны (по первому признаку).
Первый случай доказательства приведён, а остальные случае рекомендуется рассмотреть самостоятельно.

слайды 3-4 (примеры)
Знание признаков равенства треугольников может пригодиться не только на уроке, но и в повседневной жизни. Эти признаки были известны еще с давних времён, и их применяли в строительстве. И на сегодняшний день, эти знания повсеместно используются при постройке зданий, фундаментов к ним, мебельной промышленности и во многих других отраслях производства.
Зная длину двух сторон треугольника и величину угла между ними, либо длину одной стороны и величину прилежащих к ней углов, либо же зная длины всех трёх сторон треугольника, мы с лёгкостью сможем утверждать, равны треугольники или нет. Также, это может помочь при нахождении неизвестной длины одной из сторон либо величины всех трёх углов треугольника, при условии, что есть треугольник, равный этому, и нам известны его параметры.
Кроме признаков равенства треугольников, также существует известная теорема Пифагора. Её применяют, например, при необходимости определить длину стропил для крыши дома, если известна длина балки. Ещё эту теорему можно использовать при постройке фундамента, для нахождения правильных длин несущих опор, при которых угол должен быть прямым. Также, теорему Пифагора используют и операторы мобильной связи для достижения наиболее качественного сигнала и большой зоны покрытия. Теорему Пифагора можно использовать для нахождения прямого угла между двумя прямыми вообще.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5409 |
| Номер материала | 245 |