
Презентация "Свойства равнобедренного треугольника"

Краткое описание документа:
В данном уроке мы узнаем, как выглядят и какие свойства у одного вида треугольника: равнобедренного. Спросите у учащихся, известно ли кому-то, что это за фигура? При отсутствии ответа перейдите к анализу данной темы. Треугольники, их свойства и связанные с ними объекты изучает раздел планиметрии под названием геометрия. Перед тем, как мы подробно изучим свойства необходимого треугольника, важно определиться, что такое этот частный случай треугольника: равнобедренный вид.

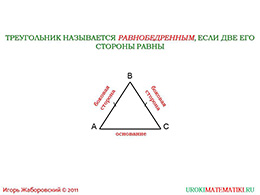
слайды 1-2 (Тема презентации "Свойства равнобедренного треугольника", пример)
Определили, что равнобедренным называется такое треугольник, у которого идентичны две его стороны. Термины и определения доступны на доске, теперь проанализируем их. В исходной фигуре «АВС» сторона «АВ» равняется стороне «ВС», именно он и является равнобедренным. Рассмотрим элементы данной фигуры. Равные «АВ» и «ВС» известны как боковые, а третья «АС» называется основанием, потому что фигура лежит на ней.
Таким образом, мы имеем частный случай общего вида.
Особенностью фигура «АВС» является то, что мы можем достроить медиану из угла «В», которая будет также треугольнику и биссектрисой, и высотой одновременно. Также стоит отметить, что углы при основании данного вида всегда будут острыми.
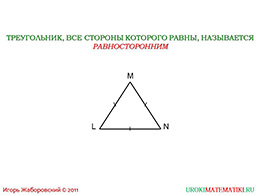
слайды 3-4 (определение равностороннего треугольника, теорема)
Если мы имеем дело с фигурой, где три стороны идентичны, то такой частный случай мы будем называть равносторонний треугольник. Градус каждого угла нашего многоугольника равняется шестидесяти градусам. Такой частный вид фигуры также известен как правильный треугольник. Отличительная особенность их – абсолютно любые высоты являются еще и медианами, и биссектрисами этой фигуры, вне зависимости от того, из какой высоты мы их строим. Если правильный треугольник вписать в окружность и описать окружность вокруг него, то центры обеих окружностей будут совпадать. Нельзя путать понятия равностороннего и равнобедренного треугольников.
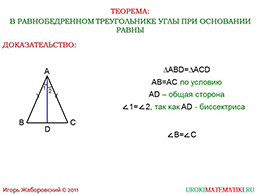
Наша цель – изучить свойства равнобедренного треугольника и, прежде всего, важную теорему. Главная теорема, с которой придётся работать при задачах на равнобедренные треугольники – это теорема, формулировка которой отображена на доске. Нам необходимо доказать равенство углов при основании, зная, что боковые стороны треугольника равны.
Для того, чтобы доказать теорему, необходимо сделать дополнительное построение и рассмотреть полученные треугольники. В нашем случае, мы используем биссектрису, которая в равностороннем треугольнике является и медианой, и высотой. Рассмотрим треугольники «АСD» и треугольник «АВD». Получается, что у треугольников есть общая сторона «АD», угол один и угол два равны, потому что «АD» является биссектрисой, ну а стороны «АВ» и «АС» равны, потому что треугольник равнобедренный. Таким образом, получаем доказательство равенства исходных двух прямоугольных треугольников.
Из равенства треугольников следует равенство углов, поэтому угол «В» равняется углу «С». Что и требовалось доказать.
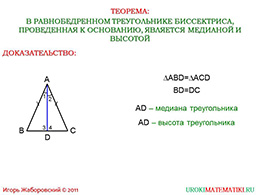

слайды 5-6 (теорема, свойства)
Далее мы углубимся в одно из наиболее приятных свойств равнобедренного треугольника. Обратим внимание на формулировки теорем.
Итак, дан равнобедренный треугольник, где «АВ» равняется «АС», а в треугольнике проведена биссектриса «АD» к основанию. Стало быть, угол один будет равен углу два.
Нам необходимо доказать, что отрезок «AD» делит противоположную сторону на две равные части и касается основания под прямым углом.
Доказательство основано на равенстве треугольников «ADB» и «АDС». Мы видим, что треугольники равны по первому признаку, потому что стороны «АВ» и «АС» идентичны по условию, высота «АD» общая, а углы один и два идентичны, потому что «АD» - биссектриса. Мы доказали теорему по двум сторонам и углу между ними.
Из равенства треугольников следует равенство всех соответствующих элементов, т.е. «BD» и «CD». Углы три и четыре равны, потому что они лежат против равных сторон. Более того, сумма этих углов равно ста восьмидесяти градусам, потому что они смежные. Следовательно, каждый из них равен девяносто градусам, то есть они прямые.
Согласно рассмотренной теореме биссектриса «АD» в нашем треугольнике является и высотой, и медианой. Поэтому справедливы следующие изречения, формулировки которых вы видите на доске.
То есть мы осознаём взаимовыгодное равенство высот, медиан и биссектрис в равнобедренном треугольнике, при условии, что они приведены к его основанию.
Итак, теперь мы знаем определение равнобедренного треугольника и различаем его свойства. Теперь можно использовать данные знания при решении типовых геометрических задач (например, на доказательство того, что треугольник равнобедренный и так далее).
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6019 |
| Номер материала | 243 |