
Урок "Медианы, биссектрисы и высоты треугольника"

Краткое описание документа:
Видеоурок «Медианы, биссектрисы и высоты треугольника» содержит информацию об основных элементах треугольников и их расположении. Основная задача данного видеоурока – проинформировать об основных элементах треугольника и их свойствах. Данная информация потребуется ученикам в решении геометрических практических задач.
Преимущества видеоурока – использование анимационных эффектов для улучшения качества обучения, повышения концентрации внимания учеников на освоении учебного материала. При изучении понятий медианы, биссектрисы и высоты данные элементы могут быть выделены цветом на рисунке для лучшего усвоения информации учениками. Видеоурок заменяет объяснение учителя по данной теме. В это время учитель имеет возможность уделить внимание индивидуальной работе с учениками.
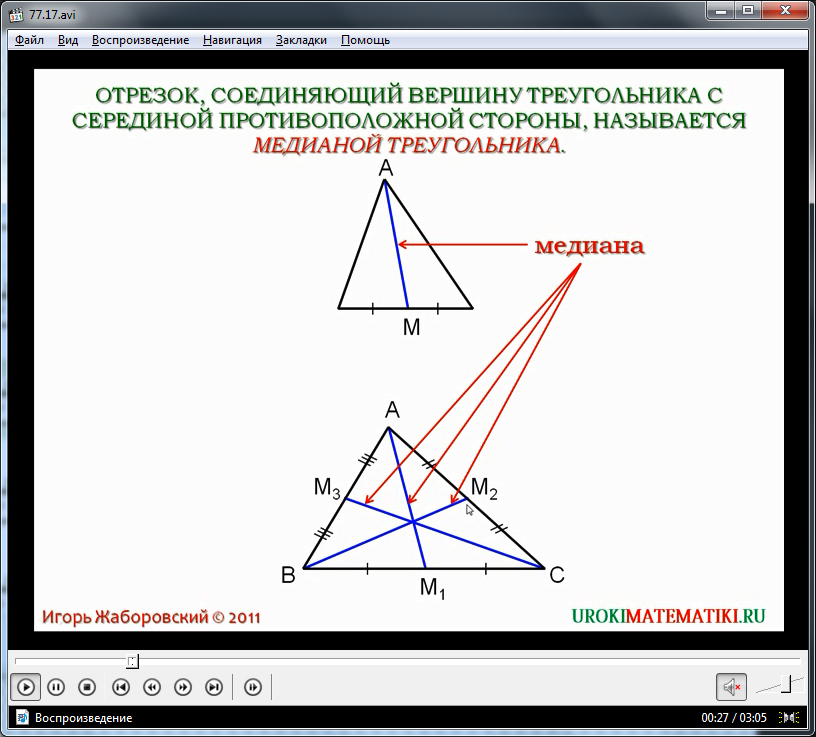
Видеоурок начинается с объявления его названия. Затем вводится определение медианы - отрезка, соединяющего вершину этого треугольника и серединную точку противоположной стороны. Ниже располагается треугольник, на котором медиана АМ выделяется синим цветам. Название элемента вынесено при помощи указателя. Ниже данного треугольника изображен треугольник со всеми медианами, которые могут быть в нем. Сообщается, что в треугольнике может быть три медианы, так как у каждого треугольника есть три вершины, из которых могут выходить медианы. В изображенном треугольнике ΔАВС построены медианы АМ1, ВМ2, СМ3. Отмечается, что точка М1 медианы разделяет сторону треугольника ВС на равные части, точка М2 – середина стороны АС, а М3 – середина стороны АВ.
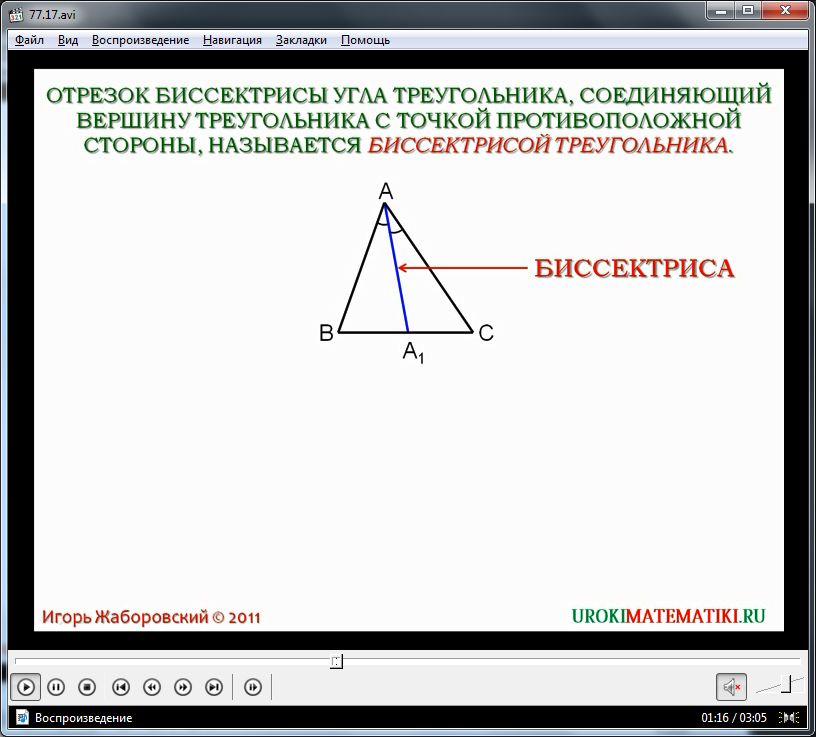
Ученики уже знакомы с понятием биссектрисы угла. Им напоминается определение биссектрисы угла - луча, исходящего из вершины, делящего угол на равные углы. Определение биссектрисы треугольника выходит из данного определения угла и является отрезком, исходящим из вершины, делящим угол пополам, соединяющим вершину рассматриваемого треугольника со стороной, лежащей напротив. Для лучшего восприятия биссектриса треугольника выделена синим цветом, а название элемента вынесено при помощи указателя для лучшего запоминания. Ниже треугольника ΔАВС с построенной биссектрисой АА1 располагается треугольник ΔCDE, в котором проведены все возможные биссектрисы. Сообщается, что любой треугольник содержит три биссектрисы. В рассматриваемом треугольнике построены биссектрисы СС1, DD1, EE1.
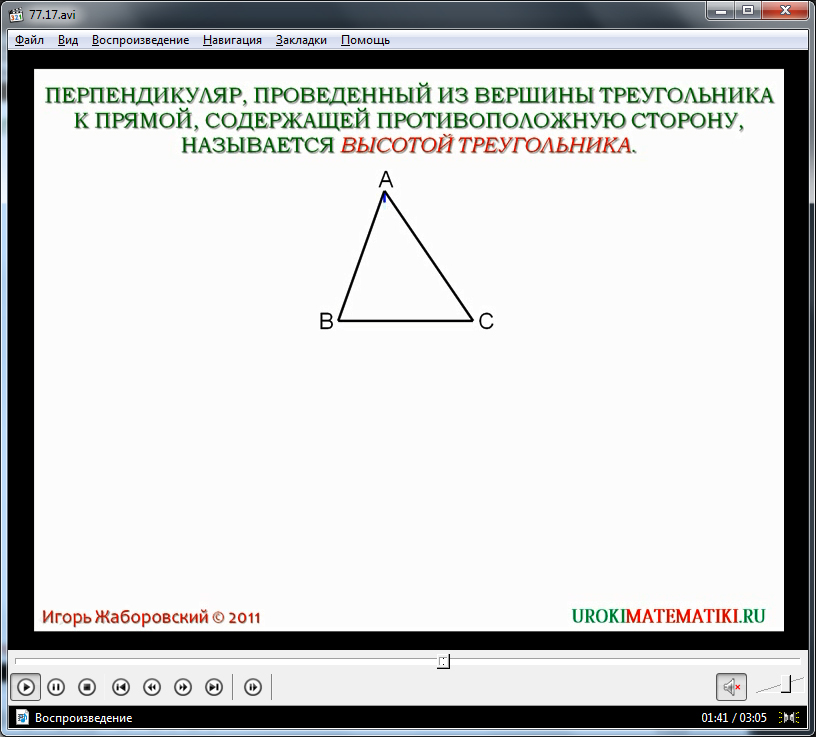
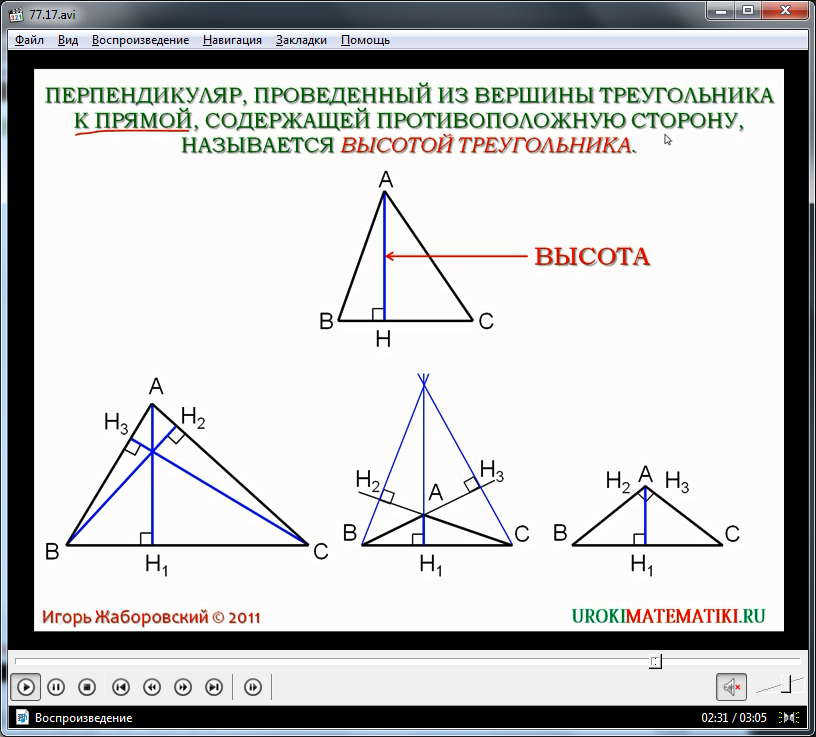
Ученики уже знакомы с понятием перпендикуляра по материалу, изученному на предыдущих уроках. На нем основано понятие высоты треугольника. Определение высоты треугольника как перпендикуляра, выходящего из вершины треугольника и опущенного на прямую, содержащую противолежащую сторону - высота треугольника. Изображение треугольника ΔАВС, в котором проведена высота АН, выделенная для отличия синим цветом, выведено на экран. Для лучшего запоминания понятия название элемента вынесено и выделено при помощи указателя. Ниже данного рисунка располагаются треугольники с проведенными перпендикулярами. Сообщается, что каждый треугольник имеет три высоты, так как в каждом треугольнике есть три вершины, из которых можно провести высоту. На рисунке в первом треугольнике построены три высоты АН1, ВН2 и СН3. На втором рисунке изображен треугольник, в котором провести перпендикуляр к противоположной стороне невозможно. В данном случае отмечается особенность проведения высоты не к противоположной стороне, а к прямой, ее содержащей. Чтобы правильно выполнить построение, через противоположную сторону проводят прямую, к которой и проводится перпендикуляр. На рисунке хорошо видно, как проводится подобное построение.
Последняя часть видеоурока посвящена замечательному свойству медиан, высот и биссектрис треугольника. Сообщается, что медианы любого треугольника будут пересекаться всегда в одной точке. Это можно увидеть на рисунке, где изображен треугольник ΔАВС, в котором изображены медианы АМ2, ВМ1, СМ3, пересекающиеся в одной точке. На следующем рисунке отображено замечательное свойство биссектрис треугольника. Сообщается, что биссектрисы также пересекаются всегда в одной точке, что изображено на треугольнике ΔCDE, где видно, как пересекаются биссектрисы СС1, DD1, ЕЕ1. Справедливость данных свойств будет доказываться на уроках геометрии в 8 классе.
Видеоурок «Медианы, биссектрисы и высоты треугольника» может быть использован на традиционном уроке в школе вместо объяснения учителем новой темы. Также данный материал может помочь в дистанционном обучении учеником или быть рекомендован для самостоятельного изучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8510 |
| Номер материала | 504 |